性能解析LMI(H∞ノルム)…Homework
[1] 直達項をもつ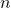 次系の
次系の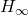 ノルムが
ノルムが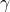 より小である条件は
より小である条件は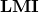 を用いて、次のように表されます。
を用いて、次のように表されます。

図1 直達項をもつn次系
実際、シュール補元に関するLMIより
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{l} \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D &-I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{cc} A^TX+XA & XB \\ B^TX & -\gamma^2 I \end{array}\right] - \left[\begin{array}{cc} C^T\\ D^T \end{array}\right] (-I) %(-\gamma^{-1} I) \left[\begin{array}{cc} C & D \end{array}\right] <0 \\ \Leftrightarrow \left[\begin{array}{cc} A^TX+XA & XB \\ B^TX & 0 \end{array}\right] < \left[\begin{array}{cc} C^T & 0 \\ D^T & I \end{array}\right] \left[\begin{array}{cc} -I & 0 \\ 0 & \gamma^2 I \end{array}\right] \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5c2560cc668d6d0690878b8eedd8885c_l3.png)
が成り立つことに注意して
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D & - I \end{array}\right]<0 \\ &\Leftrightarrow \forall \left[\begin{array}{c} x \\ u \end{array}\right]\ne0: \underbrace{ \left[\begin{array}{c} x \\ u \end{array}\right]^T \left[\begin{array}{cc} A^TX+XA & XB \\ B^TX & 0 \end{array}\right] \left[\begin{array}{c} x \\ u \end{array}\right] }_{\dot{V}(x)=\frac{d}{dt}(x^TXx)} \\ < \underbrace{ \left[\begin{array}{c} x \\ u \end{array}\right]^T \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right]^T \left[\begin{array}{cc} - I & 0 \\ 0 & \gamma^2 I \end{array}\right] \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right] \left[\begin{array}{c} x \\ u \end{array}\right] }_{s(u,y)=\gamma^2 u^Tu-y^Ty} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-474ab9036f2ca5939a3c709f1500ddf6_l3.png)
すなわち、条件
が成り立ち、これを積分して
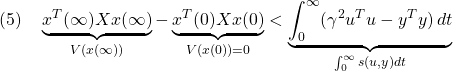
を得ます。漸近安定性より左辺は正でなければならないので
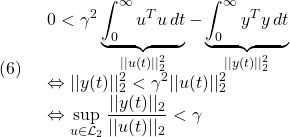
が成り立ちます。
●入力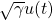 から出力
から出力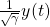 への入出力特性は不変であることから
への入出力特性は不変であることから
![Rendered by QuickLaTeX.com \displaystyle{(7) \begin{array}{l} \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D & -I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{ccc} A^TX+XA & X(B\sqrt{\gamma}) & (\frac{1}{\sqrt{\gamma}}C)^T \\ (B\sqrt{\gamma})^TX & - \gamma^2 I & D^T \\ (\frac{1}{\sqrt{\gamma}}C) & D & -I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{ccc} I & 0 & 0 \\ 0 & \sqrt{\gamma} I & 0 \\ 0 & 0 & \frac{1}{\sqrt{\gamma}} I \end{array}\right] \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D &-\gamma I \end{array}\right] \left[\begin{array}{ccc} I & 0 & 0 \\ 0 & \sqrt{\gamma} I & 0 \\ 0 & 0 & \frac{1}{\sqrt{\gamma}} I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D &-\gamma I \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9f78ef9deeaf1d5eba2e99bef8581c5e_l3.png)
を得て、次が成り立ちます。
演習B22…Flipped Classroom
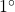 2次振動系に対して、適当な
2次振動系に対して、適当な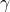 を設定し、
を設定し、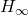 ノルムと$の大小関係をチェックするプログラムを作成せよ。
ノルムと$の大小関係をチェックするプログラムを作成せよ。
| MATLAB |
%ana_lmi5.m
%------
clear all, close all
zeta=0.4; Mp=0.5/zeta/sqrt(1-zeta^2)
A=[0 1;-1 -2*zeta]; B=[0;1];
C=[1 0]; D=0; n=2;
gam=input('gamma = ');
%------
setlmis([]);
X=lmivar(1,[n 1]);
%------
lmi1=newlmi;
lmiterm([lmi1 1 1 X],1,A,'s'); %#1:X*A+A'*X
lmiterm([lmi1 1 2 X],1,B); %#1:X*B
lmiterm([lmi1 2 2 0],-gam); %#1:-gam
lmiterm([lmi1 3 1 0],C); %#1:C
lmiterm([lmi1 3 2 0],D); %#1:D
lmiterm([lmi1 3 3 0],-gam); %#1:-gam
%------
lmi2=newlmi;
lmiterm([-lmi2 1 1 X],1,1); %#2:X
%------
LMIs=getlmis;
[tmin,xfeas]=feasp(LMIs);
X=dec2mat(LMIs,xfeas,X)
%------
%eof
|
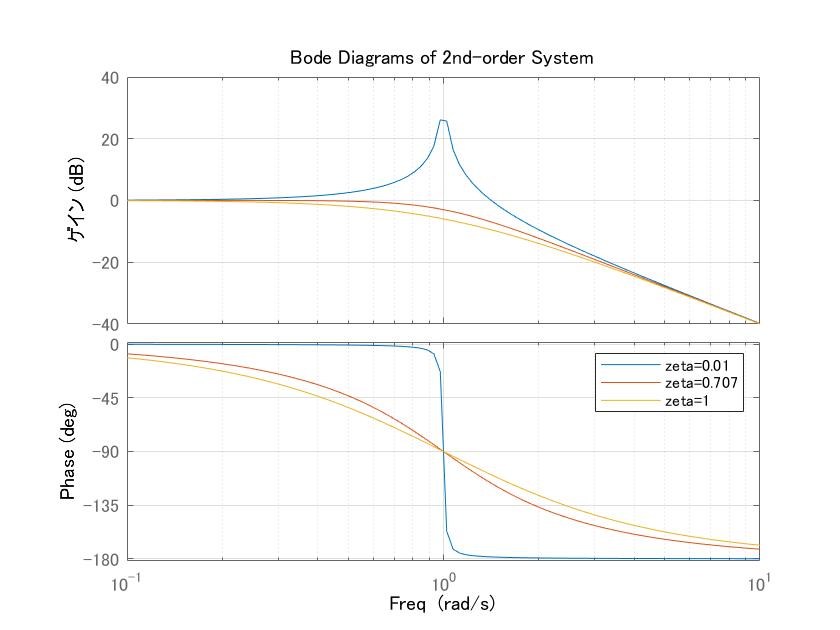
図2 2次系の周波数応答の比較
![]() 次系の
次系の![]() ノルムが
ノルムが![]() より小である条件は
より小である条件は![]() を用いて、次のように表されます。
を用いて、次のように表されます。
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \displaystyle{\sup_{u\in{\cal L}_2}\frac{||y(t)||_2}{||u(t)||_2} =\sup_{\omega\in{\rm\bf R}}||\hat{G}(j\omega)||_2<\gamma} \\ \displaystyle{\Leftrightarrow \exists X>0:\ \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D & -I \end{array}\right]<0} \\ \displaystyle{\Leftrightarrow \exists Y>0:\ \left[\begin{array}{ccc} YA^T+AY & B & YC^T \\ B^T & -\gamma^2 I & D^T \\ CY & D & -I \end{array}\right]<0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cb76514d96e7c4115d9ea88e02ad0651_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{l} \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D &-I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{cc} A^TX+XA & XB \\ B^TX & -\gamma^2 I \end{array}\right] - \left[\begin{array}{cc} C^T\\ D^T \end{array}\right] (-I) %(-\gamma^{-1} I) \left[\begin{array}{cc} C & D \end{array}\right] <0 \\ \Leftrightarrow \left[\begin{array}{cc} A^TX+XA & XB \\ B^TX & 0 \end{array}\right] < \left[\begin{array}{cc} C^T & 0 \\ D^T & I \end{array}\right] \left[\begin{array}{cc} -I & 0 \\ 0 & \gamma^2 I \end{array}\right] \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5c2560cc668d6d0690878b8eedd8885c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D & - I \end{array}\right]<0 \\ &\Leftrightarrow \forall \left[\begin{array}{c} x \\ u \end{array}\right]\ne0: \underbrace{ \left[\begin{array}{c} x \\ u \end{array}\right]^T \left[\begin{array}{cc} A^TX+XA & XB \\ B^TX & 0 \end{array}\right] \left[\begin{array}{c} x \\ u \end{array}\right] }_{\dot{V}(x)=\frac{d}{dt}(x^TXx)} \\ < \underbrace{ \left[\begin{array}{c} x \\ u \end{array}\right]^T \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right]^T \left[\begin{array}{cc} - I & 0 \\ 0 & \gamma^2 I \end{array}\right] \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right] \left[\begin{array}{c} x \\ u \end{array}\right] }_{s(u,y)=\gamma^2 u^Tu-y^Ty} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-474ab9036f2ca5939a3c709f1500ddf6_l3.png)
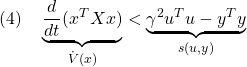
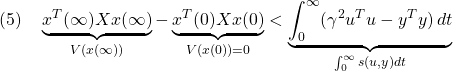
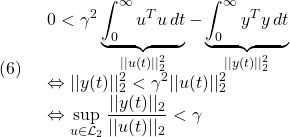
![]() から出力
から出力![]() への入出力特性は不変であることから
への入出力特性は不変であることから![Rendered by QuickLaTeX.com \displaystyle{(7) \begin{array}{l} \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D & -I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{ccc} A^TX+XA & X(B\sqrt{\gamma}) & (\frac{1}{\sqrt{\gamma}}C)^T \\ (B\sqrt{\gamma})^TX & - \gamma^2 I & D^T \\ (\frac{1}{\sqrt{\gamma}}C) & D & -I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{ccc} I & 0 & 0 \\ 0 & \sqrt{\gamma} I & 0 \\ 0 & 0 & \frac{1}{\sqrt{\gamma}} I \end{array}\right] \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D &-\gamma I \end{array}\right] \left[\begin{array}{ccc} I & 0 & 0 \\ 0 & \sqrt{\gamma} I & 0 \\ 0 & 0 & \frac{1}{\sqrt{\gamma}} I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D &-\gamma I \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9f78ef9deeaf1d5eba2e99bef8581c5e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \displaystyle{\sup_{u\in{\cal L}_2}\frac{||y(t)||_2}{||u(t)||_2} =\sup_{\omega\in{\rm\bf R}}||\hat{G}(j\omega)||_2<\gamma} \\ \displaystyle{\Leftrightarrow \exists X>0:\ \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0} \\ \displaystyle{\Leftrightarrow \exists Y>0:\ \left[\begin{array}{ccc} YA^T+AY & B & YC^T \\ B^T & -\gamma I & D^T \\ CY & D & -\gamma I \end{array}\right]<0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0e630e89fa5b93c2df2468b74a26d002_l3.png)
![]() 2次振動系に対して、適当な
2次振動系に対して、適当な![]() を設定し、
を設定し、![]() ノルムと$の大小関係をチェックするプログラムを作成せよ。
ノルムと$の大小関係をチェックするプログラムを作成せよ。