α制約LMI…Homework
[0] 自由系![]() が漸近安定であるための必要十分条件は、行列
が漸近安定であるための必要十分条件は、行列![]() の固有値がすべて複素左平面
の固有値がすべて複素左平面![]() に存在することでした。でも平衡状態
に存在することでした。でも平衡状態![]() に復帰するその過程はいつも好ましいとは言えません。たとえば、平衡状態
に復帰するその過程はいつも好ましいとは言えません。たとえば、平衡状態![]() に復帰する速さが適切であること、その過程が振動的でないこと、そして適切なサンプリング周期をもつ(絶対値が極端に大きな固有値をもたない)ことが必要です。そこで行列
に復帰する速さが適切であること、その過程が振動的でないこと、そして適切なサンプリング周期をもつ(絶対値が極端に大きな固有値をもたない)ことが必要です。そこで行列![]() の固有値が含まれる望ましい領域
の固有値が含まれる望ましい領域![]()
![]()
を考え、そのための条件を線形行列不等式![]() (Linear Matrix Inequality)で表します。
(Linear Matrix Inequality)で表します。
●準備として、次の命題をチェックします。
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]<0\\ &\Leftrightarrow& P-MQ^{-1}M^T<0,\ Q<0\\ &\Leftrightarrow& P<0,\ Q-M^TP^{-1}M<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1032be1b5ca3689d43f86d220f3f031c_l3.png) |
ここに出てくる![]() または
または![]() はシュール補元(Shure Complement)と呼ばれています。
はシュール補元(Shure Complement)と呼ばれています。
実際、次のように示されます。
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{lll} & & \underbrace{ \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right] }_{R} \\ &=& \left[\begin{array}{cc} I & MQ^{-1} \\ 0 & I \end{array}\right] \left[\begin{array}{cc} P-MQ^{-1}M^T & 0 \\ 0 & Q \end{array}\right] \left[\begin{array}{cc} I & 0 \\ Q^{-1}M^T & I \end{array}\right] \\ &=& \underbrace{ \left[\begin{array}{cc} I & 0 \\ M^TP^{-1} & I \end{array}\right] }_{T^T} \underbrace{ \left[\begin{array}{cc} P & 0 \\ 0 & Q-M^TP^{-1}M \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{cc} I & P^{-1}M \\ 0 & I \end{array}\right] }_{T} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c71f6a58283e2c1b2186c86022be5b68_l3.png)
これから
![]()
を得て、次が成り立ちます。
![]()
[1] 次の領域![]() を考えます。
を考えます。
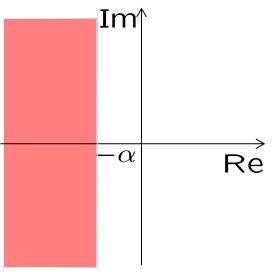
図1 領域![]()
このとき、次の命題が成り立ちます。
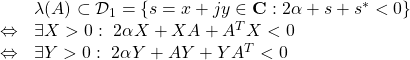 |
●実際、まず領域![]() が上図を表すことは、次のように確かめられます。
が上図を表すことは、次のように確かめられます。
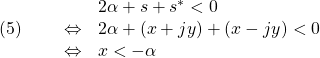
●次に、十分性は、![]() とすると、次のように確かめられます(*は複素共役)。
とすると、次のように確かめられます(*は複素共役)。
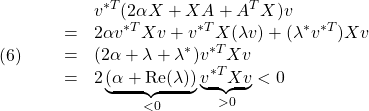
さらに、![]() とおくと、次が成り立ちます。
とおくと、次が成り立ちます。
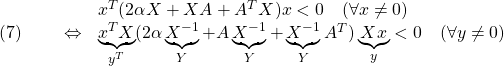
必要性については、あとで述べます。
演習B11…Flipped Classroom
![]() α制約を調べる次のコードを説明せよ。
α制約を調べる次のコードを説明せよ。
| MATLAB |
|
Note B11 Inversion Lemma
![]()
![]()
![]()
および
![]()
![]()
![]()
が成り立つことから、次を得ます。
![]()
![]()
特に、次が成り立ちます。
![]()