リャプノフの安定定理
[1] 非線形システム理論に関する文献:
Hassan K.Khalil: Nonlinear Systems, 3rd ed., Prentice Hall, 2002
から次の定理(Theorem 4.1, p.114)を引用します。
|
リャプノフの安定定理 状態方程式
に対して、その平衡状態
このとき
ならば、平衡状態
ならば、平衡状態 |
すなわち、(2)と(4)を満足するリャプノフ関数![]() の存在を示して(発見して)、非線形系(1)の漸近安定性を示すことができます。
の存在を示して(発見して)、非線形系(1)の漸近安定性を示すことができます。
●振り子の例について、エネルギーの変化と安定性の関係を考えてみます。その運動方程式は,摩擦力を入れた場合
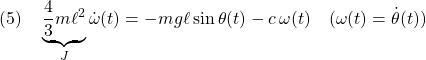
です。いま、運動エネルギーと位置エネルギーの和を
![]()
と書くと、(5)を用いて
![]()
が成り立ちます。このようにエネルギーが減少することは、振り子の揺れが止まることと対応するので、エネルギーの時間変化率から安定性を判定できそうです。
リャプノフの安定定理は十分条件であり、リャプノフ関数が見つからないからといって安定性や漸近安定性が成り立たないとはかぎりません。また、リャプノフ関数の構築法について一般論はないのですが、上でみたようにエネルギーとの関連が深いです。そこで、振り子の平衡状態
![]()
の安定性を調べるために、(6)のエネルギー![]() をリャプノフ関数の候補としてみます。まず、(6)と(7)から、
をリャプノフ関数の候補としてみます。まず、(6)と(7)から、![]() は
は![]() の安定性を保証するためのリャプノフ関数といえます。
の安定性を保証するためのリャプノフ関数といえます。
つぎに、(7)から
![]()
ですが、これは![]() が
が![]() は漸近安定性を保証するためのリャプノフ関数とはならないことを示しています。しかし、実際は漸近安定なので、ほかにリャプノフ関数の候補を探せる可能性があります。
は漸近安定性を保証するためのリャプノフ関数とはならないことを示しています。しかし、実際は漸近安定なので、ほかにリャプノフ関数の候補を探せる可能性があります。
例えば、エネルギー![]() の代わりに、つぎのリャプノフ関数の候補を考えます。
の代わりに、つぎのリャプノフ関数の候補を考えます。
![]()
この時間微分を計算すると、(5)を用いて
![]()
となります。ここで
![]()
だから、(11)は負値をとります。したがって、(10)はリャプノフ関数となっています。
[2] リャプノフの安定定理を線形系
![]()
に適用して、漸近安定性を保証するリャプノフ関数を求めてみます。その候補として次を考えます。
![]()
これを微分して(17)を用いると
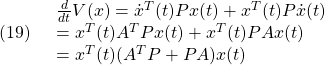
となります。したがって、線形行列不等式
![]()
が成り立てば、(2)と(4)が満足され、線形系(17)の漸近安定性が成り立つといえます。
●逆に、もし線形系(17)が漸近安定、すなわち
![]()
であれば、線形行列不等式(20)を満たす![]() を次のように決めることができます。
を次のように決めることができます。
![]()
ここで、![]() は任意です(ある条件下では
は任意です(ある条件下では![]() としてもよい)。実際
としてもよい)。実際
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \begin{array}{l} \displaystyle{A^T\int_0^\infty \exp(A^Tt)Q\exp(At)dt+\int_0^\infty \exp(A^Tt)Q\exp(At)dt\,A}\\ \displaystyle{=\int_0^\infty \frac{d}{dt}(\exp(A^Tt)Q\exp(At))\,dt}\\ \displaystyle{=\left[\exp(A^Tt)Q\exp(At)\right]_0^\infty=-Q<0} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8818d2570a2394fee7a40d1e57a29ee2_l3.png)
となって(20)を満足します。また、任意の![]() に対して
に対して
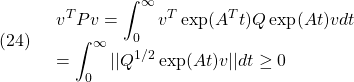
ですが、![]() とすると、
とすると、![]() が得られ、これは
が得られ、これは![]() を意味し矛盾です。したがって
を意味し矛盾です。したがって![]() でなけれならず、
でなけれならず、![]() を得ます。以上から、線形行列不等式(20)が(17)の漸近安定性の必要十分条件になっています。
を得ます。以上から、線形行列不等式(20)が(17)の漸近安定性の必要十分条件になっています。
●(20)において、![]() 、
、![]() とおくと、漸近安定性の等価な条件として次が得られます。
とおくと、漸近安定性の等価な条件として次が得られます。
![]()
![]()
本資料では同様な多くのLMIが登場しますが、(25)のタイプをX-LMI、(26)のタイプをY-LMIと呼びます。X-LMIは特性解析のために、Y-LMIはコントローラ設計(シンセシス)のために使い分けられます。
演習B02…Flipped Classroom
![]() 安定行列
安定行列![]() に対して、線形行列不等式(20)を満足する正定行列
に対して、線形行列不等式(20)を満足する正定行列![]() は、次のプログラムで計算できることを確かめよ。
は、次のプログラムで計算できることを確かめよ。
| MATLAB |
|