パラメータ変動システム…Homework
[1] 次図のような回転体の運動を考えます。
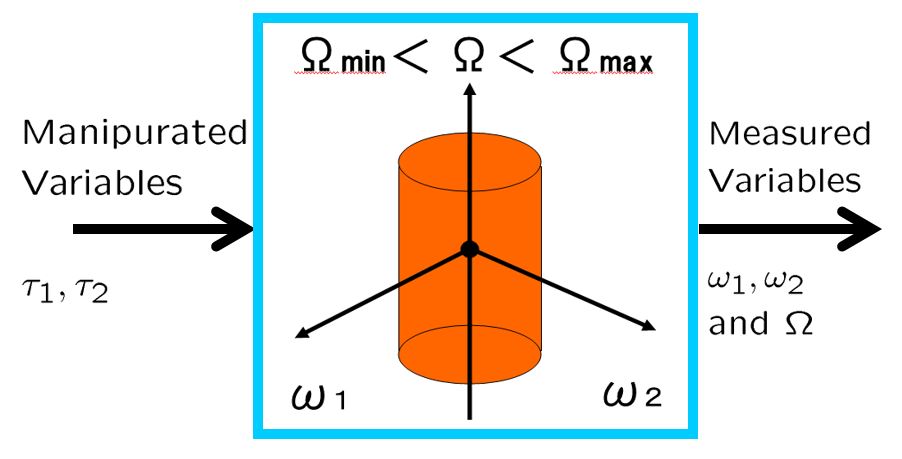 図1 パラメータ変動システムの例
図1 パラメータ変動システムの例
これは次の運動方程式で表されます。
![]()
ここで、次のパラメータ変動を想定します。
![]()
次の状態方程式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(3) \underbrace{ \left[\begin{array}{c} \dot{\omega}_1(t) \\ \dot{\omega}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & \Omega(t)\frac{J_2-J_3}{J_1} \\ \Omega(t)\frac{J_3-J_1}{J_2} & 0 \end{array}\right] }_{A(\Omega(t))} \underbrace{ \left[\begin{array}{c} \omega_1(t) \\ \omega_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} \frac{1}{J_1} & 0 \\ 0 & \frac{1}{J_2} \end{array}\right] }_{B} \underbrace{ \left[\begin{array}{c} \tau_1(t) \\ \tau_2(t) \end{array}\right] }_{u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-06d0d0706f122470d4466143aac157d2_l3.png)
●いま、![]() として
として
![]()
のようなパラメータ変動下での零入力応答をシミュレーションしてみます。
 図2 パラメータ変動システムの応答シミュレーション例
図2 パラメータ変動システムの応答シミュレーション例
もしパラメータ変動がない場合はきれいな正弦波となりますから、パラメータ変動がある場合はかなりの動特性の変動が表れています。
演習B01…Flipped Classroom
![]() 図2のグラフを描け。
図2のグラフを描け。
| MATLAB |
|
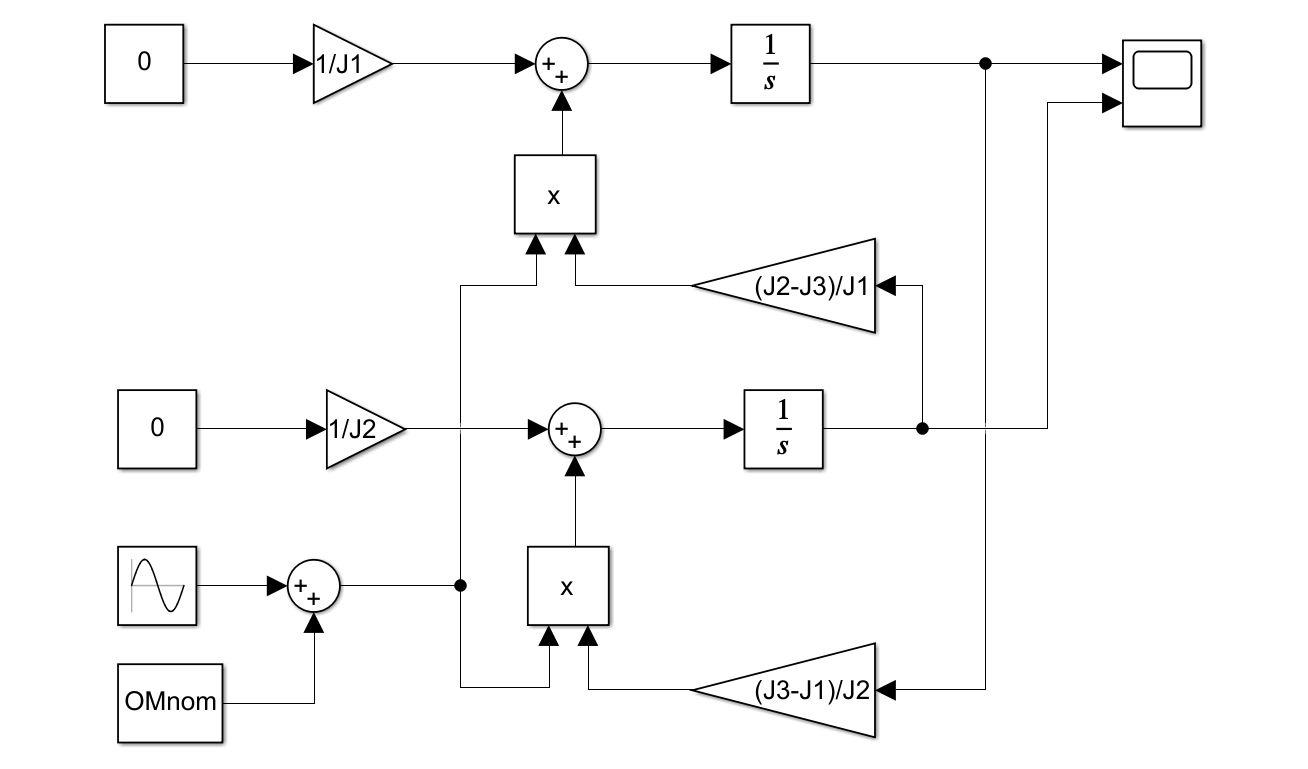 図3 SPIN0.slx
図3 SPIN0.slx
Note B01 パラメータ変動システムの応答シミュレーション

このSimulinkブロック線図は
![]()
を次式のように書き換えて、Productを利用したものです。
![]()
それでは演習B01のSPIN.slxはどのように構成すればよいでしょうか?