LQGI制御 | 制御系CAD

LQGI制御…Homework

[1]　可制御かつ可観測な $n$ 次系を考えます。

$\displaystyle{(1)\quad \dot{x}(t)=Ax(t)+Bu(t)+w\quad(x(t),w\in{\bf R}^n,u(t)\in{\bf R}^m) }$

$\displaystyle{(2)\quad y(t)=C_Mx(t)\quad(y(t)\in{\bf R}^p) }$

ここで、状態方程式には、操作入力 $u(t)$ のほかに、定値外乱 $w$ が加わっていること、出力方程式における行列 $C$ を $C_M$ と書いたことに注意します。いま、出力変数の一部やそれらの組合せからなる新しい $m$ 個の被制御変数を

$\displaystyle{(3)\quad z(t)=C_Sy(t)=\underbrace{C_SC_M}_{C}x(t)\quad(z(t)\in{\bf R}^m) }$

のように選び( $(A,C)$ は可観測対)、定値外乱があるにも拘わらず、制御目的

$\displaystyle{(4)\quad z(t)\ \rightarrow\ r \quad (t\rightarrow\infty) }$

を達成したいとします。ここで、定数ベクトル $r$ は $m$ 個の設定値からなる。もし制御目的(4)が物理的に可能とすると、ある状態 $x_\infty$ と入力 $u_\infty$ が確定し

$\displaystyle{(5)\quad \left[\begin{array}{c} -w \\ r \end{array}\right] = \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right] }$

の関係を満足しているはずです。したがって、どのような $w$ と $r$ に対しても、 $x_\infty$ と $u_\infty$ が定まるように、被制御変数(3)を

$\displaystyle{(6)\quad {\rm rank}\, \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S}=n+m }$

が成り立つように選ぶものとします。

●さて、制御目的(4)を達成するために、つぎの積分動作を加えた状態フィードバックを考えました。

$\displaystyle{(7)\quad u(t)=-Fx(t)-F_Ix_I(t)}$

ただし

$\displaystyle{(8)\quad \dot{x}_I(t)=z(t)-r \qquad (x_I(0)=0) }$

実際には、式(7)の代わりに、状態オブザーバ

$\displaystyle{(9)\quad \dot{\hat{x}}(t)=(A-HC_M)\hat{x}(t)+Hy(t)+Bu(t) }$

の出力を用いて

$\displaystyle{(10)\quad u(t)=-F\hat{x}(t)-F_Ix_I(t) }$

を実施することになります。ここでの積分動作を加えたオブザーバベースコントローラは、(10)を(9)に代入した

$\displaystyle{(11)\quad \dot{\hat{x}}(t)=(A-HC_M-BF)\hat{x}(t)-BF_Ix_I(t)+Hy(t) }$

と、(8)を合わせて、つぎのように表されます。

$\displaystyle{(12)\quad \boxed{\begin{array}{rl} \left[\begin{array}{c} \dot{\hat{x}}(t) \\ \dot{x}_I(t) \end{array}\right] =& \underbrace{ \left[\begin{array}{cc} A-HC_M-BF & -BF_I \\ 0 & 0 \end{array}\right] }_{A_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right]\\[10mm] &+ \underbrace{ \left[\begin{array}{cc} H & 0\\ C_S & -I_m \end{array}\right] }_{B_K} \left[\begin{array}{c} y(t) \\ r \end{array}\right] \end{array}} }$

$\displaystyle{(13)\quad \boxed{u(t)= \underbrace{- \left[\begin{array}{cc} F & F_I \end{array}\right] }_{C_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right]} }$

これによる閉ループ系は、(10)を(1)に代入した

$\displaystyle{(14)\quad \dot{x}(t)=Ax(t)-BF\hat{x}(t)-BF_Ix_I(t)+w(t) }$

と、(8)、(3)を合わせて

$\displaystyle{(15)\quad \boxed{\left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\ \dot{\hat{x}}(t) \end{array}\right] = \left[\begin{array}{ccc} A & -BF_I & -BF \\ C & 0 & 0 \\ HC_M & -BF_I & A-HC_M-BF \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r \\ 0 \end{array}\right]} }$

のように表されます。そのブロック線図を図1に示します。

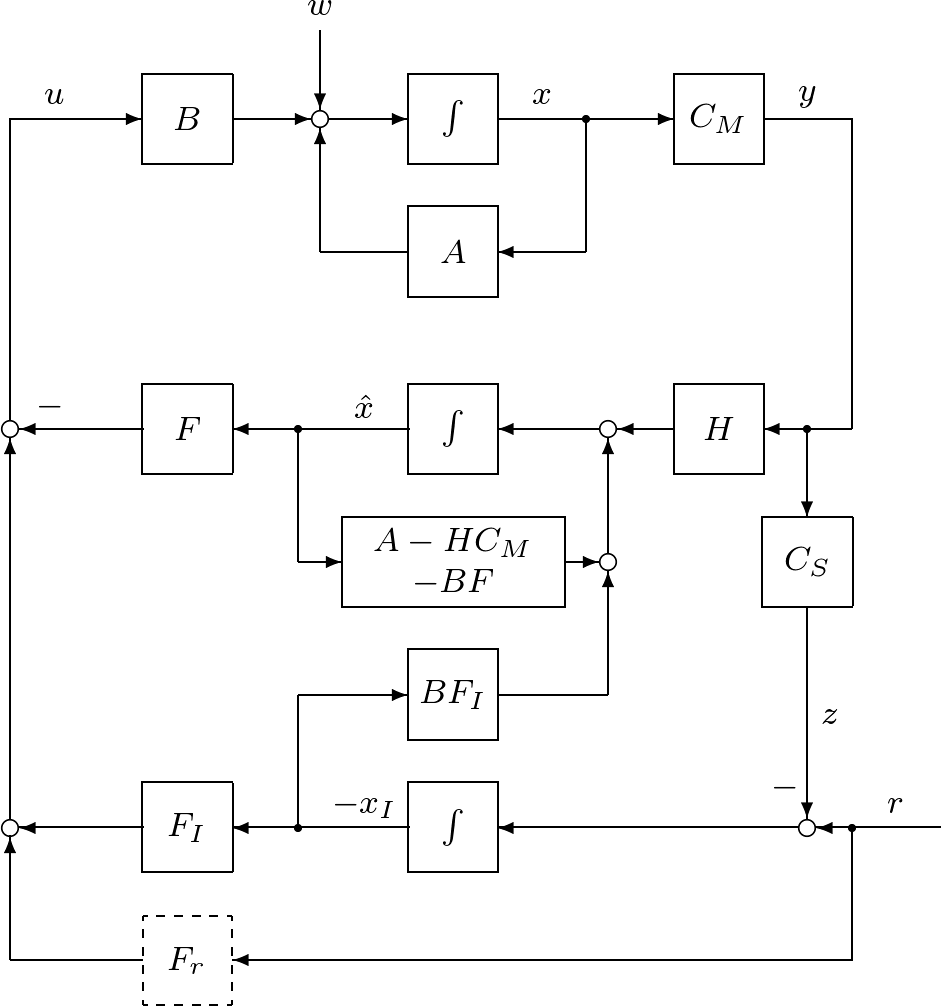図1 積分動作を加えたオブザーバベースコントローラによる閉ループ系

●いま、閉ループ系(15)に、座標変換

$\displaystyle{(16)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\ e(t) \end{array}\right] = \left[\begin{array}{ccc} I_n & 0 & 0 \\ 0 & I_m & 0 \\ -I_n & 0 & I_n \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] }$

を行えば

$\displaystyle{(17)\quad \boxed{\left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\\hline \dot{e}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} A-BF & -BF_I & -BF \\ C & 0 & 0 \\\hline 0 & 0 & A-HC_M \end{array}\right] }_{ A_{EF}'= \left[\begin{array}{c|c} A_{EF} & - \left[\begin{array}{cc} B \\ 0 \end{array}\right] F \\[5mm] \hline 0 & \widehat{A} \end{array}\right] } \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r \\\hline -w \end{array}\right]} }$

となり、閉ループ系の固有値は、積分動作を加えた状態フィードバックだけの閉ループ系の固有値と状態オブザーバの固有値からなります。

ここで、 $A_{EF}$ は安定行列であるとします。このとき、(17)より

$\displaystyle{(18)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] \ \rightarrow\ \underbrace{ \left[\begin{array}{c|c} A_{EF}^{-1} & -A_{EF}^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] F\widehat{A}^{-1} \\[5mm]\hline 0 & \widehat{A}^{-1} \end{array}\right] }_{A_{EF}'\,^{-1}} \left[\begin{array}{c} -w \\ r \\\hline w \end{array}\right] \quad (t\rightarrow\infty) }$

ここで

$\displaystyle{(19)\quad S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] = \left[\begin{array}{cc} 0 \\ I_m \end{array}\right] }$

$\displaystyle{(20)\quad A_{EF}^{-1} = \left[\begin{array}{cc} I_n & 0 \\ -F_I^{-1}F & -F_I^{-1} \end{array}\right] S^{-1} }$

を用いて

$\displaystyle{(21)\quad x(t)\ \rightarrow\ x_\infty \quad (t\rightarrow\infty) }$

$\displaystyle{(22)\quad -F_Ix_{I}(t)\ \rightarrow\ F(x_\infty+e_\infty)+u_\infty \quad (t\rightarrow\infty) }$

$\displaystyle{(23)\quad e(t)\ \rightarrow\ e_\infty=\widehat{A}^{-1}w \quad (t\rightarrow\infty) }$

を得ます。したがって、定値外乱が存在するときは状態オブザーバに関して定常偏差が残るにもかかわらず、制御目的(4)が成り立つことがわかります。

[2]　以下に、偏差系E3をLQG制御により安定化して、積分動作を加えたオブザーバベースコントローラを構成する手順を示します。

アルゴリズム　＜LQGI制御＞

ステップ1　被制御変数の決定

$\left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]$ が正則となるように( $C=C_SC_M$ )、セレクタ行列 $C_S(m\times p)$ を決めます。

ステップ2　偏差系の安定化

偏差系

$\displaystyle{(24)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E}} {\dot u}(t) }$

を、状態フィードバック

$\displaystyle{(25)\quad {\dot u}(t)=- \left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }$

によるLQ制御で安定化します。その際、評価関数としては

$\displaystyle{(26)\quad \int_0^\infty \left( \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]^T Q_E \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] +{\dot u}^T(t)R_E{\dot u}(t)\right)\,dt }$

を用いる。ただし、 $(A_E,Q_E^{\frac{1}{2}})$ は可観測対とします。

さらに、 $F$ と $F_I$ を、次式から計算します。

$\displaystyle{(27)\quad \left[\begin{array}{cc} F & F_I \end{array}\right] = \left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]^{-1} }$

ステップ3　オブザーバゲイン $H$ の決定

行列 $B'$ を、 $(A,B')$ が可制御対となるように選び、重み行列 $W>0$ と $V>0$ を指定し

$\displaystyle{(28)\quad \Gamma A^T+A\Gamma-\Gamma C_M^TV^{-1}C_M\Gamma+B'WB'^T=0 }$

を解いて、 $\Gamma>0$ を求め、オブザーバゲイン $H$ をつぎのように定めます。

$\displaystyle{(29)\quad H=V^{-1}C_M\Gamma }$

ステップ4　LQGIコントローラの構成

$C_S$ 、 $F$ 、 $F_I$ 、 $H$ から、つぎを構成します。

$\displaystyle{(30)\quad \dot{x}_K(t)=A_Kx_K(t)+B_K \left[\begin{array}{c} y(t) \\ r \end{array}\right] }$

$\displaystyle{(31)\quad u(t)=C_Kx_K(t) }$

ただし

$\displaystyle{(32)\quad A_K= \left[\begin{array}{cc} A-HC_M-BF & -BF_I \\ 0\,(m\times n) & 0\,(m\times m) \end{array}\right] }$

$\displaystyle{(33)\quad B_K= \left[\begin{array}{cc} H & 0\,(n\times m)\\ C_S & -I_m \end{array}\right] }$

$\displaystyle{(34)\quad C_K=- \left[\begin{array}{cc} F & F_I \end{array}\right] }$

この手順で設計された積分動作を加えた状態フィードバックによる制御方式をLQGI制御(LQG control with integral action)と呼びます。