状態フィードバック

状態フィードバック…Homework

[1]　ある平衡状態周りの挙動が線形状態方程式

$\displaystyle{(1)\quad \dot{x}(t)=Ax(t)+Bu(t)\quad(x(t)\in{\rm\bf R}^n,u(t)\in{\rm\bf R}^m) }$

で表される制御対象に対して、状態フィードバック

$\displaystyle{(2)\quad \boxed{u(t)=-Fx(t)} }$

を考えます。ここで、 $m$ を入力変数の個数、 $n$ を状態変数の個数とするとき、 $F$ はサイズ $m\times n$ のゲイン行列です。(2)を(1)に代入して、次式を得ます。

$\displaystyle{(3)\quad \boxed{\dot{x}(t)=(A-BF)x(t)} }$

以上の状況は次図のように図示されます。

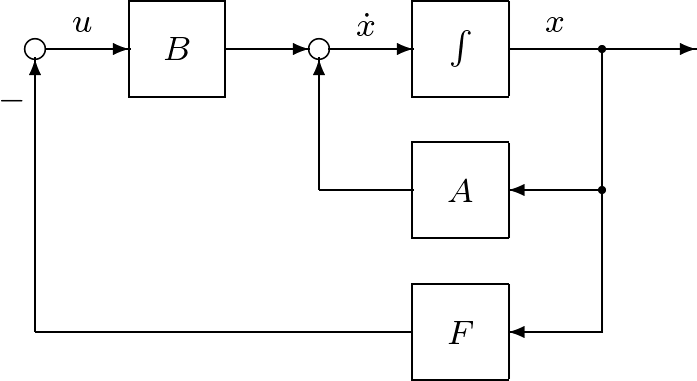図1 状態フィードバックによる閉ループ系

これは、制御対象とコントローラ（状態フィードバック）が閉路を構成することから、閉ループ系と呼ばれます。ここで、興味深いのは、制御対象が不安定であっても（行列 $A$ の固有値の一部が複素左半平面にあっても）、状態フィードバックを行って閉ループ系を構成すると、行列 $A-BF$ の固有値をすべて複素左半平面に移動させる可能性があることです。どのような条件の下で、どのようにゲイン行列 $F$ を決定できるかを検討する問題を状態フィードバックによる安定化問題と言います。

●状態フィードバックゲイン行列 $F$ を求めることは、適当な安定行列 $A_{F}$ を与えて、行列方程式

$\displaystyle{(4)\quad A-BF=A_F\Leftrightarrow BF=A-A_F }$

を解くことに他なりません。よく学生さんは次のように解きます。

$\displaystyle{(5)\quad F=B^{-1}(A-A_F) }$

でも一般には $B$ は正方行列ではないので、そもそも逆行列を考えることができません。 $A_F$ を安定行列とする状態フィードバックが求まる条件の説明は次節で行いますが、ここではその準備として、状態フィードバックゲイン行列 $F$ を求める公式を示します。

[2]　いま行列 $A_F=A-BF$ の特性多項式を次式で表します。

$\displaystyle{(6)\quad {\rm det}(\lambda I_n-A_F)=\lambda^n+a_1'\lambda^{n-1}+\cdots+a_n' %=(\lambda-\lambda_1')\times\cdots\times(\lambda-\lambda_n') }$

ケーリーハミルトンの定理から次式が成り立ちます。

$\displaystyle{(7)\quad A_F^n+a_1'A_F^{n-1}+\cdots+a_{n-1}'A_F+a_n'I_n=0_{n\times n} }$

これは $n=2$ のとき、次のように書けます。

$\displaystyle{(8)\quad \begin{array}{l} A_F^2+a_1'A_F+a_2'I_2=0\\ \quad\Downarrow\\ (A-BF)A_F+a_1'(A-BF)+a_2'I_2=0\\ \quad\Downarrow\\ AA_F-BFA_F+a_1'A-a_1'BF+a_2'I_2=0\\ \quad\Downarrow\\ A(A-BF)+a_1'A+a_2'I_2=BFA_F+a_1'BF\\ \quad\Downarrow\\ A^2+a_1'A+a_2'I_2=BF(A_F+a_1'I_2)+ABF\\ \quad\Downarrow\\ A^2+a_1'A+a_2'I_2=\left[\begin{array}{ccc} B &AB \end{array}\right] \left[\begin{array}{ccc} F(A_F+a_1'I_2)\\ F \end{array}\right] \end{array} }$

したがって、１入力系で $\left[\begin{array}{ccc} B &AB \end{array}\right]$ が正則ならば、次の公式を得ます。

$\displaystyle{(9)\quad \boxed{F= \left[\begin{array}{ccc} 0 &1 \end{array}\right] \left[\begin{array}{ccc} B &AB \end{array}\right]^{-1} (A^2+a_1'A+a_2'I_2)} }$

同様に、 $n=3$ のとき、次のように書けます。

$\displaystyle{(10)\quad \begin{array}{l} A_F^3+a_1'A_F^2+a_2'A_F+a_3'I_3=0\\ \quad\Downarrow\\ (A-BF)(A_F^2+a_1'A_F+a_2'I_3)+a_3'I_3=0\\ \quad\Downarrow\\ A(A_F^2+a_1'A_F+a_2'I_3)+a_3'I_3\\=BF(A_F^2+a_1'A_F+a_2'I_3)\\ \quad\Downarrow\\ A((A-BF)A_F+a_1'(A-BF)+a_2'I_3)+a_3'I_3\\=BF(A_F^2+a_1'A_F+a_2'I_3)\\ \quad\Downarrow\\ A^2(A-BF)+a_1'A^2+a_2'A+a_3'I_3\\ =BF(A_F^2+a_1'A_F+a_2'I_3)+ABF(A_F+a_1'I_3)\\ \quad\Downarrow\\ A^3+a_1'A^2+a_2'A+a_3'I_3\\ =BF(A_F^2+a_1'A_F+a_2'I_3)+ABF(A_F+a_1'I_3)+A^2BF\\ \quad\Downarrow\\ A^3+a_1'A^2+a_2'A+a_3'I_3\\ =\left[\begin{array}{ccc} B &AB&A^2B \end{array}\right] \left[\begin{array}{ccc} F(A_F^2+a_1'A_F+a_2'I_3)\\ F(A_F+a_1'I_3)\\ F \end{array}\right] \end{array} }$

したがって、１入力系で $\left[\begin{array}{ccc} B &AB&A^2B \end{array}\right]$ が正則ならば、次の公式を得ます。

$\displaystyle{(11)\quad F= \left[\begin{array}{ccc} 0 &0 &1 \end{array}\right] \left[\begin{array}{ccc} B &AB&A^2B \end{array}\right]^{-1} (A^3+a_1'A^2+a_2'A+a_3'I_3) }$

$n>3$ の場合も同様にして、 $A_F=A-BF$ の特性多項式(7)を

$\displaystyle{(12)\quad %\begin{array}{l} A^n+a'_1A^{n-1}+\cdots+a'_nI_n =\left[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}\right] \left[\begin{array}{ccc} X_{n-1}\\ \vdots\\ X_1\\ F \end{array}\right] %\end{array} }$

のように書き換えることができます。ここで、 $X_1,\cdots,X_{n-1}$ はサイズ $m\times n$ の適当な行列です。したがって、１入力系で $\left[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}\right]$ が正則ならば、(12)の右辺の第２番目の行列の最下段にある $F$ を取りだすことにより、次の公式が得られます。

$\displaystyle{(13)\quad \boxed{\begin{array}{l} F= \left[\begin{array}{cccc} 0 & \cdots & 0 & 1 \end{array}\right] \left[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}\right]^{-1}\\ \times (A^n+a'_1A^{n-1}+\cdots+a'_nI_n) \end{array}} }$

このように、１入力 $n$ 次系の場合は、 $F$ の $n$ 個の要素が、 $A-BF$ の特性多項式の $n$ 個の係数（すなわち $n$ 個の固有値）を指定することにより決定されます。ところが $m$ 入力系の場合、 $A_F$ の固有値だけでは決まらず、対応する固有ベクトルまで指定する必要があります。このことを以下で調べてみます。

[3]　いま、ジョルダン分解 $A_F=V\Lambda V^{-1}$ を仮定して

$\displaystyle{(14)\quad A-BF=\underbrace{V\Lambda V^{-1}}_{A_F} \Rightarrow AV-V\Lambda=B\underbrace{FV}_{G} }$

ここで、 $\Lambda$ が対角行列の場合、 $A_F$ の固有値 $\lambda_1',\cdots,\lambda_n'$ に対応する固有ベクトルを $v_1,\cdots,v_n$ として

$\displaystyle{(15)\quad A \underbrace{ \left[\begin{array}{ccc} v_1&\cdots&v_n \end{array}\right] }_{V} - \underbrace{ \left[\begin{array}{ccc} v_1&\cdots&v_n \end{array}\right] }_{V} \underbrace{ {\rm diag}\{\lambda_1',\cdots,\lambda_m'\} }_{\Lambda}=}$

$\displaystyle{ \left[\begin{array}{ccc} (A-\lambda_1'I_n)v_1&\cdots&(A-\lambda_n'I_n)v_n \end{array}\right] =B \underbrace{ \left[\begin{array}{ccc} g_1&\cdots&g_n \end{array}\right] }_{G} }$

これより、もし $\lambda_1',\cdots,\lambda_n'$ が $A$ の固有値と一致しないならば、固有ベクトルの表現式として次式を得ます。

$\displaystyle{(16)\quad \underbrace{ \left[\begin{array}{ccc} v_1&\cdots&v_n \end{array}\right] }_{V}= \left[\begin{array}{ccc} (A-\lambda_1'I_n)^{-1}Bg_1&\cdots&(A-\lambda_n'I_n)^{-1}Bg_n \end{array}\right] }$

したがって、状態フィードバックゲイン行列 $F$ を求める次の手順が考えられます。

1) $A_F$ の固有値 $\lambda_1',\cdots,\lambda_n'$ を $A$ の固有値とは異なるように指定する。

2) $A_F$ の固有ベクトル $v_1,\cdots,v_n$ を決める自由度 $g_1,\cdots,g_n$ を、(15)の $V$ が正則になるように与える。

3) 次式で $F$ を求める。

$\displaystyle{(17)\quad \boxed{F=GV^{-1}} }$

この手順は簡潔ですが、１）の制約があること、２）の具体的な手法が不明であることなどの難点があります。状態フィードバックを定める手続きは、ある最適化問題の解として得ることが多く、これについてはあと説明します。

演習 A31…Flipped Classroom

$1^\circ$ 次のコードを実行し、 $A-BF$ の固有値を計算し、指定されているものになっていることを確かめよ。

MATLAB

%a31_1.m
%-----
 clear all, close all
 A=[0 1;0 0]; B=[0;1]; p=[-1 -1];
 F=sf(A,B,p)
 lambda=eig(A-B*F)
%----- 
 A=[1 2;3 4]; B=[5;6]; p=[-1+i -1-i];
 F=sf(A,B,p)
 lambda=eig(A-B*F)
%----- 
 function F=sf(A,B,p)
   n=size(A,1); r=eig(A);
   a=[1 -r(1)]; for i=2:n, a=conv(a,[1 -r(i)]); end, a=a(n+1:-1:2);
   b=[1 -p(1)]; for i=2:n, b=conv(b,[1 -p(i)]); end, b=b(n+1:-1:2);
   X=zeros(n,n); for i=1:n, X(i,1:n-i+1)=[a(i+1:n) 1]; end
   Y=B; for i=2:n, Y=[B A*Y]; end
   F=real((b-a)/X/Y);
 end
%-----
%eof

$2^\circ$ 次のコードを実行し、 $A-BF$ の固有値と固有ベクトルを計算し、指定されているものになっていることを確かめよ。

MATLAB

%a31_2.m
%-----
 clear all, close all
 A=[0 0;0 -1]; B=[1 1;1 -1]; p=[-2 -3]; V=[1 0;0 1];
 [n,m]=size(B);
 G=[];
 for i=1:n, G=[G ((A-p(i)*eye(n,n))\B)\V(:,i)]; end
 F=G/V
 [V,R]=eig(A-B*F)
%-----
%eof

Note A31 不可制御の例
どのような制御対象に対しても，閉ループ系を安定化する状態フィードバックが求まるわけではありません。たとえば、皆さんは小さいころ棒立て遊びをやった記憶があると思います。不安定なモノを安定化できた楽しい思い出だったと思います。それでは、２本の棒を同時に立てることはできたと思いますか？この状況を次図のように表します。

図２本の棒立て制御

ここで、２本の棒の長さと質量をそれぞれ $\ell_1,\ell_2$ と $m_1,m_2$ とします。また鉛直線からの傾きを $\theta_1,\theta_2$ とします。２本の棒は１つの軸に取り付けられており、自由に回転できるとします。この軸を左右に動かして回転トルクを与えるのですが、その結果として働くトルクをここでは $h_1\tau, h_2\tau$ で表します。このとき運動方程式は次式となります。ただし、 $J_1=\frac{4}{3}m_1\ell_1^2, J_2=\frac{4}{3}m_2\ell_2^2$ 。

$\displaystyle{(1)\quad \left\{\begin{array}{l} J_1\ddot\theta_1(t)=m_1g\ell_1\theta_1(t)+h_1\tau(t) \\ J_2\ddot\theta_2(t)=m_1g\ell_2\theta_2(t)+h_2\tau(t) \end{array}\right. }$

これから次の状態方程式を得ます。

$\displaystyle{(2)\quad \begin{equation} \frac{d}{dt} \left[\begin{array}{c} \theta_1\\ \theta_2\\ \dot\theta_1\\ \dot\theta_2\\ \end{array}\right]= \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ a_1 & 0 & 0 & 0\\ 0 & a_2 & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} \theta_1\\ \theta_2\\ \dot\theta_1\\ \dot\theta_2\\ \end{array}\right]+ \left[\begin{array}{c} 0\\ 0\\ b_1\\ b_2\\ \end{array}\right]\tau }$

ただし、 $a_1=\frac{3g}{4\ell_1}, a_2=\frac{3g}{4\ell_2}$ 、 $b_1=\frac{h_1}{J_1}, b_2=\frac{h_2}{J_2}$ 。

それでは、これを安定化する状態フィードバックゲインを求めてみます。上述の公式

$\displaystyle{(3)\quad F= \left[\begin{array}{cccc} 0 & \cdots & 0 & 1 \end{array}\right] %\underbrace{ \left[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}\right]^{-1} %}_{可制御性行列} }$

を参照すれば、次の行列が正則である必要があります。

$\displaystyle{(4)\quad \begin{equation} \left[\begin{array}{cccc} B & AB & A^2B & A^3B \end{array}\right] = \left[\begin{array}{cccc} 0 &b_1 &0 &a_1b_1\\ 0 &b_2 &0 &a_2b_2\\ b_1&0 &a_1b_1 &0\\ b_2&0 &a_2b_2 &0\\ \end{array}\right] }$

これは２つの棒の長さ違うときは正則となり、閉ループ系を安定化する状態フィードバックが求まります。ところが２つの棒が同じで、 $a_1=a_2, b_1=b_2$ となる場合は、第１行と第２行が同じとなり、第３行と第４行も同じとなり、正則性は失われます。これから全く同じ２本の棒の棒立ては成功しないと考えられます。これは「二兎を追うものは一兎も得ず」のことわざ通りですね。

制御系CAD

制御を意識したモノつくりを目指して

状態フィードバック