2次系の周波数応答…Homework
[1] 次のようにパラメタライズされた漸近安定な1入力1出力2次系の状態空間表現を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(1a)\quad \underbrace{ \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ K\omega_n^2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2c38bce5a54dbe22b2c1cfbb9ac7882a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1b)\quad y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f5e291f6df4bf13c895efeb7714483d4_l3.png)
ここで、![]() とします。また以下では簡単のため
とします。また以下では簡単のため![]() とします。このときインパルス応答は、次式で与えられました。
とします。このときインパルス応答は、次式で与えられました。
![]()
![]()
この2次系に対して、正弦波入力
![]()
を考えます。2次振動系(![]() )の場合、零状態応答は次式で与えられます(導出は Note A24-2を参照)。
)の場合、零状態応答は次式で与えられます(導出は Note A24-2を参照)。
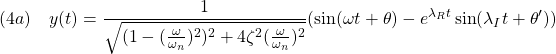
![]()
![]()
ここで、![]() とすると
とすると
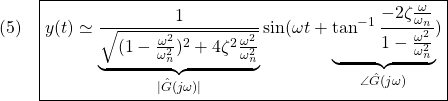
ただし
![]()
これは、入力が正弦波のときは、時間が十分立てば、出力も正弦波となることを示しています。その振幅と位相はそれぞれ![]() の絶対値と偏角となっています。
の絶対値と偏角となっています。
![]() をゲイン、
をゲイン、![]() を位相と呼びます。このゲイン線図と位相線図をペアにして片対数グラフにプロットしたものをボード線図と呼びます。ゲインはdb値(
を位相と呼びます。このゲイン線図と位相線図をペアにして片対数グラフにプロットしたものをボード線図と呼びます。ゲインはdb値(![]() )、位相はdeg値(
)、位相はdeg値(![]() )です。
)です。
実際、2次系において![]() のとき、ボード線図を描いてみると次のグラフが得られます
のとき、ボード線図を描いてみると次のグラフが得られます
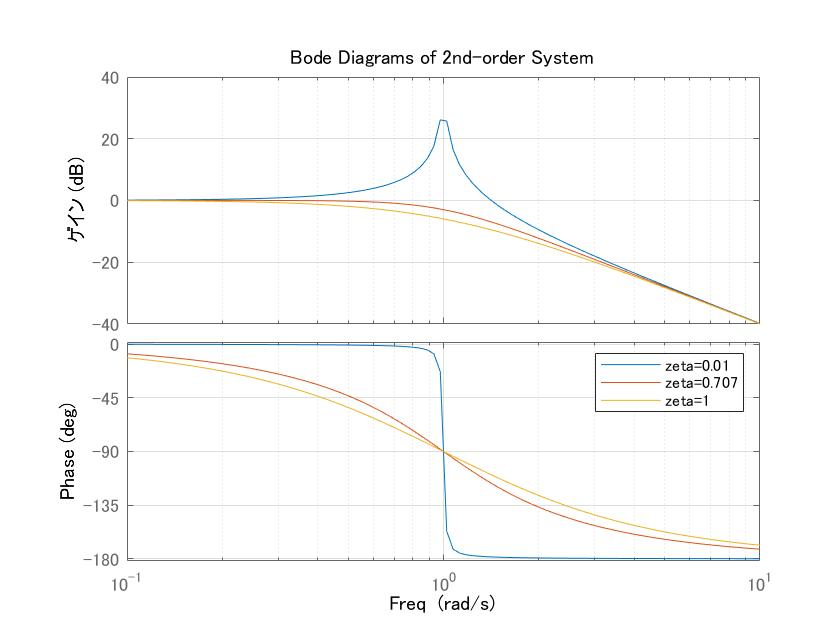 図1 2次系の周波数応答の比較
図1 2次系の周波数応答の比較
周波数応答に基づく2次系の同定…Homework
[2] 2次振動系の場合、ゲイン線図
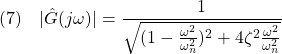
の頂点は次式で与えられます。
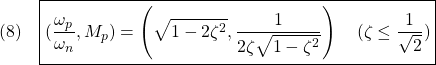
ここで、頂点が現れる条件、![]() がついていることに注意してください。
がついていることに注意してください。
実際、![]() を満足する
を満足する![]() は
は
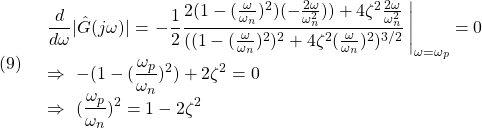
となって、次式のように表されます。
![]()
また、このときの最大値は
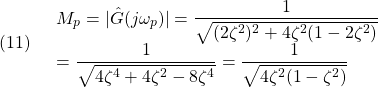
となって、次式のように表されます。。
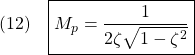
(10)と(12)から、2次振動系はゲイン線図が頂点を持つ場合、その座標![]() を求めて、減衰係数と固有角周波数
を求めて、減衰係数と固有角周波数![]() が得られることを示しています。
が得られることを示しています。
●ちなみに、![]() を満足する帯域幅
を満足する帯域幅![]() は次のように計算されます。
は次のように計算されます。
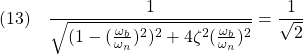
において、![]() とおくと
とおくと
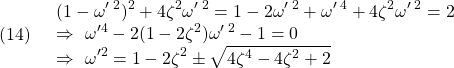
となって、次式のように表されます。
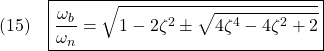
演習A24…Flipped Classroom
図1のゲイン曲線#1を描け。
| MATLAB |
|
| SCILAB |
|
Note A24-1 n次系の周波数応答
次の漸近安定な1入力1出力![]() 次系の状態空間表現を考えます。
次系の状態空間表現を考えます。
![]()
このとき、正弦波入力
![]()
に対する零状態応答を計算します。そのために
![]()
を、零状態応答の式
![]()
に代入して
![Rendered by QuickLaTeX.com (5)\quad \begin{array}{l} \displaystyle{y(t)=\int_0^tC\exp(A(t-\tau))Be^{j\omega\tau}d\tau}\\ \displaystyle{=C\exp(At)\int_0^te^{j\omega\tau}\exp(-A\tau)Bd\tau}\\ \displaystyle{=C\exp(At)\int_0^t\exp(j\omega\tau I_n)\exp(-A\tau)Bd\tau}\\ \displaystyle{=C\exp(At)\int_0^t\exp((j\omega I_n-A)\tau)Bd\tau}\\ \displaystyle{=C\exp(At) \left[\frac{}{}\exp((j\omega I_n-A)\tau)\right]_0^t(j\omega I_n-A)^{-1}B}\\ \displaystyle{=C\exp(At) (\exp((j\omega I_n-A)t)-I_n)(j\omega I_n-A)^{-1}B}\\ \displaystyle{=-C\exp(At)(j\omega I_n-A)^{-1}B+C\exp(At)\exp(j\omega t I_n)\exp(-At)(j\omega I_n-A)^{-1}B}\\ \displaystyle{=-C\exp(At)(j\omega I_n-A)^{-1}B+C(j\omega I_n-A)^{-1}Be^{j\omega t}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cf72e1d083b5093019ffc1a9ae42a3ca_l3.png)
ここで![]() とすると
とすると
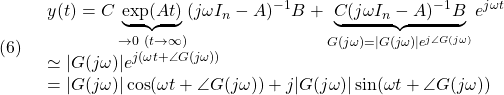
これから正弦波入力(3)に対する零状態応答は、![]() のとき次式で与えられます。
のとき次式で与えられます。
![]()
これは、入力が正弦波のときは、時間が十分立てば、出力も正弦波となることを示しています。その振幅と位相はそれぞれ![]() の絶対値と偏角となっています。
の絶対値と偏角となっています。
Note A24-2 2次系の周波数応答
次の2次系を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(1a)\quad \underbrace{ \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b716bd0f77f40c082b3d8efd7314fe4f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1b)\quad y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f5e291f6df4bf13c895efeb7714483d4_l3.png)
ここで、![]() とします。このときインパルス応答は
とします。このときインパルス応答は
![]()
![]()
でした。いま、正弦波入力
![]()
に対する時間応答を考えます。このとき、公式
![]()
![]()
![]()
![]()
を用いて、周波数応答が次のように得られます。
![Rendered by QuickLaTeX.com (5)\quad \begin{array}{l} \displaystyle{y(t)=\int_0^t\frac{\omega_n^2}{\lambda_I}e^{\lambda_R(t-\tau)}\sin\lambda_I(t-\tau)\sin\omega\tau\,d\tau}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\sin\lambda_It\int_0^te^{-\lambda_R\tau}\sin\omega\tau\cos\lambda_I\tau\,d\tau}\\ \displaystyle{-\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\cos\lambda_It\int_0^te^{-\lambda_R\tau}\sin\omega\tau\sin\lambda_I\tau\,d\tau}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\sin\lambda_It\times}\\ \displaystyle{(\left[\frac{e^{-\lambda_R\tau}(-\lambda_R\sin(\omega+\lambda_I)\tau-(\omega+\lambda_I)\cos(\omega+\lambda_I)\tau)}{2(\lambda_R^2+(\omega+\lambda_I)^2)}\right.}\\ \displaystyle{+\left.\frac{e^{-\lambda_R\tau}(-\lambda_R\sin(\omega-\lambda_I)\tau-(\omega-\lambda_I)\cos(\omega-\lambda_I)\tau)}{2(\lambda_R^2+(\omega-\lambda_I)^2)}\right]_0^t)}\\ \displaystyle{-\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\cos\lambda_It\times}\\ \displaystyle{(\left[-\frac{e^{-\lambda_R\tau}(-\lambda_R\cos(\omega+\lambda_I)\tau+(\omega+\lambda_I)\sin(\omega+\lambda_I)\tau)}{2(\lambda_R^2+(\omega+\lambda_I)^2)}\right.}\\ \displaystyle{+\left.\frac{e^{-\lambda_R\tau}(-\lambda_R\cos(\omega-\lambda_I)\tau+(\omega-\lambda_I)\sin(\omega-\lambda_I)\tau)}{2(\lambda_R^2+(\omega-\lambda_I)^2)^2}\right]_0^t)}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\sin\lambda_It\times}\\ \displaystyle{(\frac{e^{-\lambda_Rt}(-\lambda_R\sin(\omega+\lambda_I)t-(\omega+\lambda_I)\cos(\omega+\lambda_I)t)+\omega+\lambda_I}{2(\lambda_R^2+(\omega+\lambda_I)^2)}}\\ \displaystyle{+\frac{e^{-\lambda_Rt}(-\lambda_R\sin(\omega-\lambda_I)t-(\omega-\lambda_I)\cos(\omega-\lambda_I)t)+\omega-\lambda_I}{2(\lambda_R^2+(\omega-\lambda_I)^2)})}\\ \displaystyle{-\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\cos\lambda_It\times}\\ \displaystyle{(\frac{-e^{-\lambda_Rt}(-\lambda_R\cos(\omega+\lambda_I)t+(\omega+\lambda_I)\sin(\omega+\lambda_I)t)-\lambda_R}{2(\lambda_R^2+(\omega+\lambda_I)^2)}}\\ \displaystyle{+\frac{e^{-\lambda_Rt}(-\lambda_R\cos(\omega-\lambda_I)t+(\omega-\lambda_I)\sin(\omega-\lambda_I)t)+\lambda_R}{2(\lambda_R^2+(\omega-\lambda_I)^2)})} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0862d7bcce2485ad411ad20ffd65abfd_l3.png)
さらに変形すると

これを、公式
![]()
![]()
を用いて、以下のように変形します。
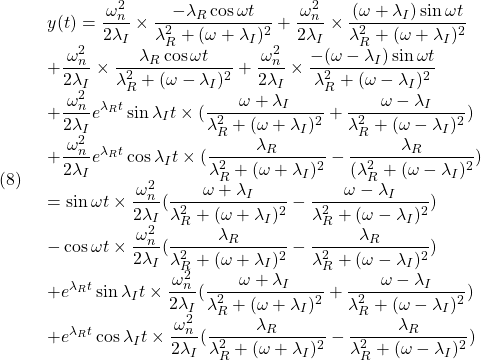
ここで
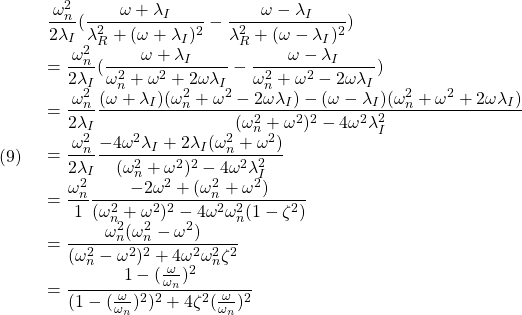
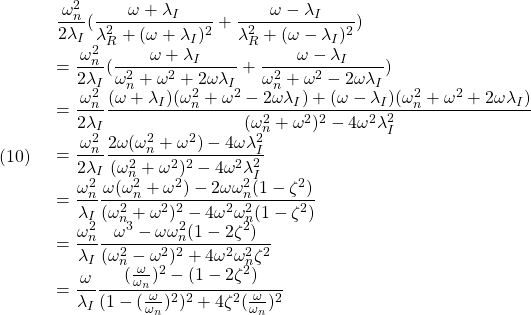
および
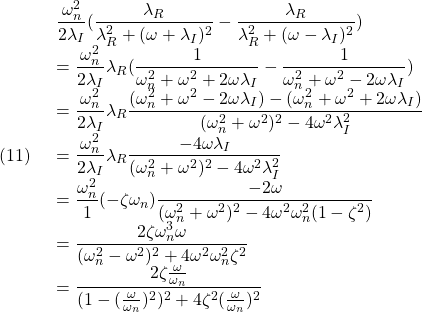
だから
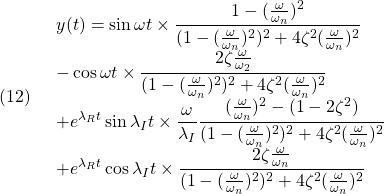
すなわち、周波数応答は
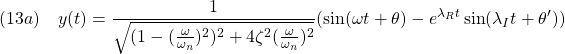
![]()
![]()
のように表されます。