平衡状態回りの線形化…Homework
[0] 制御を考えるときは、まず対象の平衡状態(equilibrium state)を念頭におきます。そして何らかの要因でこの平衡状態が乱されたとき、元の平衡状態に戻すことが制御の基本的な役割と考えられます。制御の対象としては、力学系、電気系、化学系など様々なものがあり、その振舞いはサイエンスによってすでに十分検討されています。しかし、平衡状態を保持したり、遷移させたりという対象への働きかけは、エンジニアリングの範疇となります。人が楽に操れるドローンや1輪車というモノ作りは、制御という技術がなければ達成できなかったと言えます。
●制御系設計を確実に実施・達成するための方法として次図に示すHILS アプローチが知られています。
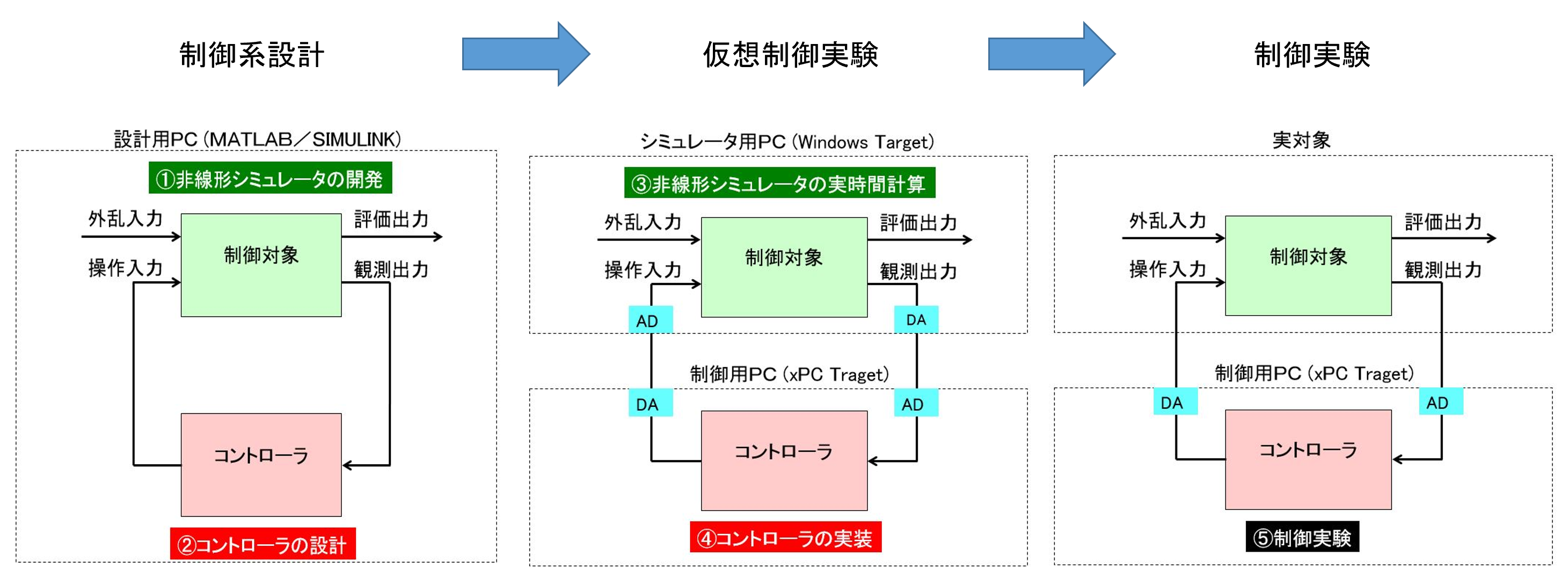 図1 HILS アプローチ
図1 HILS アプローチ
これから、制御系設計、仮想制御実験、制御実験とステップを踏むことが分かります。2台のPCを用いて実時間での閉ループシミュレーションを行う仮想制御実験の成否が決め手となるので、HILS:Hardware In the Loop Simulationがキーワードとなったと思われます。ただ、最初のステップである制御系設計を1台のPC上で十分検討することが大切であることは述べるまでもありません。制御系設計は①非線形シミュレータの開発と②コントローラの設計からなります。以下では、非線形シミュレータの開発について、
![]() 運動方程式の導出(数式処理の利用)
運動方程式の導出(数式処理の利用)
![]() 平衡状態の検討(fsolveの利用)
平衡状態の検討(fsolveの利用)
![]() 非線形状態方程式の導出(S-functionの作成)
非線形状態方程式の導出(S-functionの作成)
![]() 非線形シミュレータの開発(平衡状態の保持)
非線形シミュレータの開発(平衡状態の保持)
![]() 線形化(linmodの利用)
線形化(linmodの利用)
![]() 線形シミュレータの開発
線形シミュレータの開発
の手順を具体的に説明しますが、その前に非線形系と線形系の振舞いは平衡状態周りではどう違うのかについて振り子を例にとって説明します。
[1] 高校の物理で出てきた次の単振り子を考えます。これは吊り荷を下げたクレーンの振止めの問題を考えるのに役立ちます。
 図2 単振り子
図2 単振り子
左側に示すように鉛直線に沿って垂れ下がった状態が平衡状態です。右側に示すように重りを手で(ひもが緩まないように)持ち上げて離したときの運動方程式は
![]()
で与えられます。ここで、![]() は振り子の長さ、
は振り子の長さ、![]() は重りの質量、
は重りの質量、![]() は重力加速度、
は重力加速度、![]() は時刻
は時刻![]() における振り子の鉛直線となす角度を表しています。初期時刻
における振り子の鉛直線となす角度を表しています。初期時刻![]() では
では![]() とします。
とします。
これは簡単な微分方程式のように思えますが、そうではありません。実際、
![]()
のように展開できますから、運動方程式は
![]()
となるのですが、これは手計算では手の付けようもありません。しかしながら、![]() が十分小さく、高次項が無視できれば
が十分小さく、高次項が無視できれば
![]()
となって、解は次式で表されます。
![]()
2つの運動方程式(1)と(4)の違いを数値シミュレーションで見てみると、図3のようになります。初期角度が10![]() のときは(平衡状態近傍では)両者に差異は見られませんが、90
のときは(平衡状態近傍では)両者に差異は見られませんが、90![]() のときは周期が一致しません。また初期角度が177
のときは周期が一致しません。また初期角度が177![]() のときのシミュレーションを行ってみると、両者の差異に愕然することでしょう。
のときのシミュレーションを行ってみると、両者の差異に愕然することでしょう。
 図3 単振り子の振動シミュレーション(モデルが線形か非線形か、初期状態を平衡状態周辺にとるかによる相違)
図3 単振り子の振動シミュレーション(モデルが線形か非線形か、初期状態を平衡状態周辺にとるかによる相違)
演習A12-1…Flipped Classroom
次のコードを用いて、図2のシミュレーションを行え。
| MATLAB |
|
| SCILAB |
|
<ヒント> (1)と(4)は次のような連立1階微分方程式として表せることに注意。
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \underbrace{ \left[\begin{array}{l} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{l} \omega(t) \\ -\frac{g}{L}\sin\theta(t) \end{array}\right] }_{f(x(t))} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ded67215525ba40fa5155a4367ed7405_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{ \left[\begin{array}{l} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{g}{L}&0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{l} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ed5a0aa97035fe65dba8b64944a4a569_l3.png)
[2] 制御対象として次図に示す水タンクを例にとって、非線形シミュレータの開発手順を説明します。
 図4 水タンクTANK
図4 水タンクTANK
![]() 運動方程式の導出(数式処理の利用)
運動方程式の導出(数式処理の利用)
時刻![]() における水位、流入量、流出量をそれぞれ
における水位、流入量、流出量をそれぞれ![]() 、
、![]() 、
、![]() とします。タンクの断面積を
とします。タンクの断面積を![]() とすると、運動方程式は次式となります。
とすると、運動方程式は次式となります。
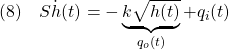
![]() 平衡状態の検討(fsolveの利用)
平衡状態の検討(fsolveの利用)
(8)から平衡状態![]() と平衡入力
と平衡入力![]() が次式のように求まります。
が次式のように求まります。
![]()
![]() 非線形状態方程式の導出(S-functionの作成)
非線形状態方程式の導出(S-functionの作成)
(8)から次の非線形状態方程式を得ます。
![]()
![]() 非線形シミュレータの開発(平衡状態の保持)
非線形シミュレータの開発(平衡状態の保持)
(10)に基づいて制御対象TANKの平衡状態周りの挙動を模擬する非線形シミュレータを次図のように構成します。
 図5 TANKの非線形シミュレータ
図5 TANKの非線形シミュレータ
一般に、制御目的が平衡状態の安定化であれば、非線形シミュレータの入力側では平衡入力を加え、出力側では平衡状態を差し引いておきます。このとき、
「零入力![]() に対して零状態
に対して零状態![]() が出力される」
が出力される」
はずですから、非線形シミュレータが正しく開発されているかのチェックに役立ちます。
![]() 線形化(linmodの利用)
線形化(linmodの利用)
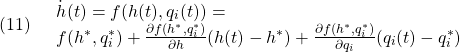
から、次の線形状態方程式を得ます。
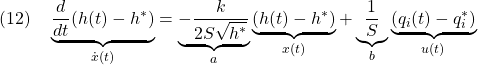
![]() 線形シミュレータの開発
線形シミュレータの開発
(12)に基づいて制御対象TANKの線形シミュレータを次図のように構成します。
 図6 TANKの線形シミュレータ
図6 TANKの線形シミュレータ
●![]() のとき、水位
のとき、水位![]() の平衡状態にあるとします。今、バケツで水を入れたため、水位が
の平衡状態にあるとします。今、バケツで水を入れたため、水位が![]() になったとします。このとき、平衡状態に戻る過程を非線形シミュレータと線形シミュレータで比較した結果を図7に示します。
になったとします。このとき、平衡状態に戻る過程を非線形シミュレータと線形シミュレータで比較した結果を図7に示します。
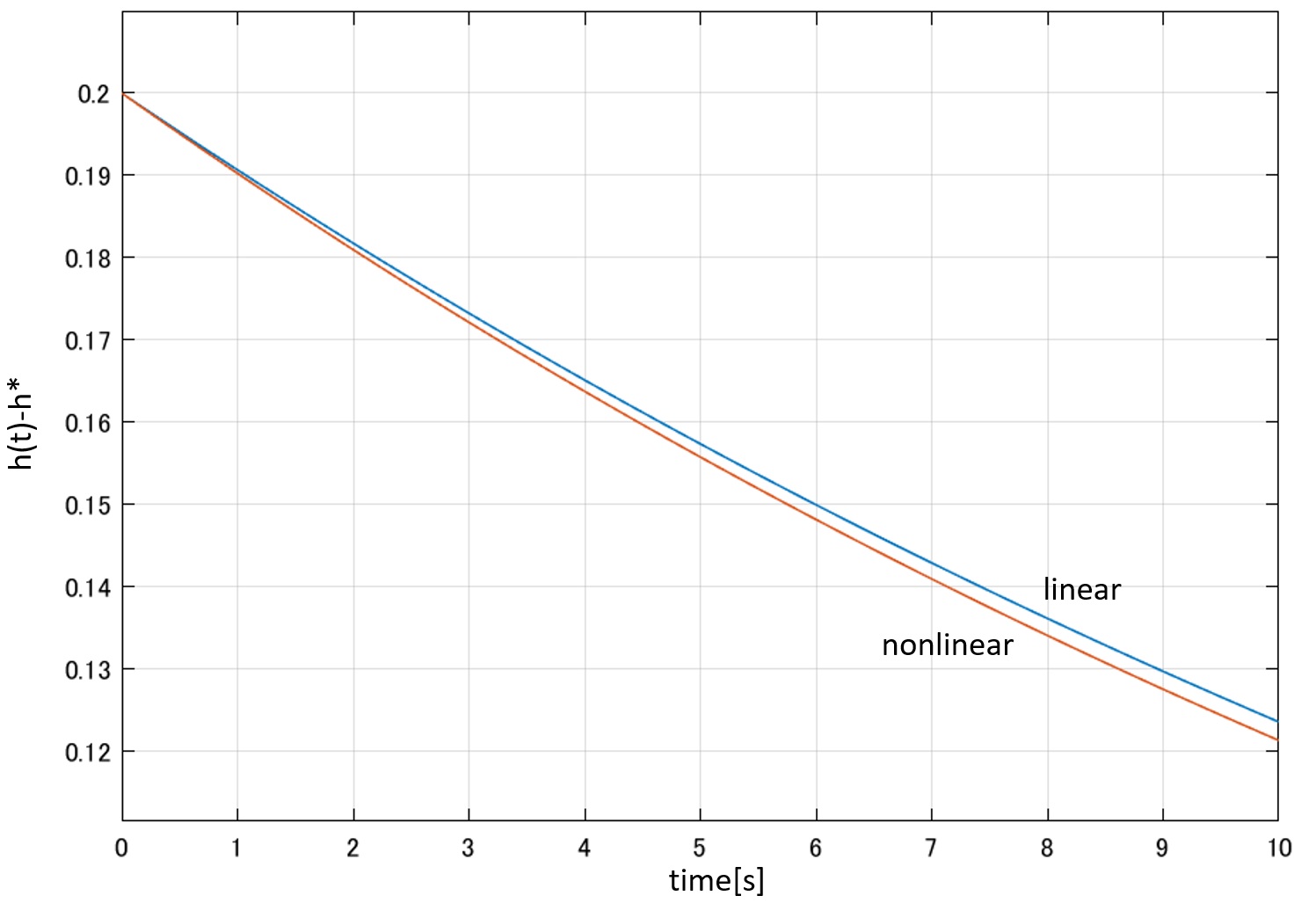 図7 TANKの非線形応答と線形応答の比較
図7 TANKの非線形応答と線形応答の比較
演習A12-2…Flipped Classroom
Simulinkを用いて図8を開発し、図7のグラフを描け。
 図8 TANKの非線形シミュレータと線形シミュレータ
図8 TANKの非線形シミュレータと線形シミュレータ
<ヒント>
| Simulink |
|
| MATLAB |
|
[3] 一般には、制御対象の運動方程式から、非線形状態方程式を求め、これを平衡状態と平衡入力まわりで線形化(1次近似)し、線形状態方程式を求めます。
いま、![]() を状態変数、
を状態変数、![]() を入力変数として、運動方程式から、次のような連立1階微分方程式で表される非線形状態方程式を得ます。
を入力変数として、運動方程式から、次のような連立1階微分方程式で表される非線形状態方程式を得ます。
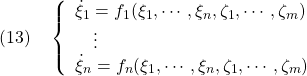
これを次のようにベクトル表示します。![]() が状態変数ベクトル、
が状態変数ベクトル、![]() が入力変数ベクトルです。
が入力変数ベクトルです。
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \boxed{\dot{\xi}=f(\xi,\zeta)}\ \Leftrightarrow\ \underbrace{ \left[\begin{array}{l} \dot{\xi}_1 \\ \vdots \\ \dot{\xi}_n \end{array}\right] }_{\dot{\xi}} = \underbrace{ \left[\begin{array}{l} f_1(\xi,\zeta) \\ \quad\vdots \\ f_n(\xi,\zeta) \end{array}\right] }_{f(\xi,\zeta)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-92634287f13e8775d2c2a6ec25c7567c_l3.png)
平衡状態![]() と平衡入力
と平衡入力![]() は
は
![]()
を満足するベクトルとして規定されます。これらの周りで![]() を1次近似すると次式を得ます。
を1次近似すると次式を得ます。
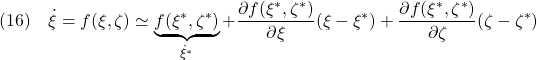
ただし
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad A=\frac{\partial\,f(\xi^*,\zeta^*)}{\partial\,\xi}= \left[\begin{array}{ccc} \frac{\partial f_1(\xi^*,\zeta^*)}{\partial \xi_1}&\cdots& \frac{\partial f_1(\xi^*,\zeta^*)}{\partial \xi_n}\\ \vdots&\ddots&\vdots\\ \frac{\partial f_n(\xi^*,\zeta^*)}{\partial \xi_1}&\cdots& \frac{\partial f_n(\xi^*,\zeta^*)}{\partial \xi_n} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9cbb1299b9fef4d94b388578973f2dd3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad B=\frac{\partial\,f(\xi^*,\zeta^*)}{\partial\,\zeta}= \left[\begin{array}{ccc} \frac{\partial f_1(\xi^*,\zeta^*)}{\partial \zeta_1}&\cdots& \frac{\partial f_1(\xi^*,\zeta^*)}{\partial \zeta_m}\\ \vdots&\ddots&\vdots\\ \frac{\partial f_n(\xi^*,\zeta^*)}{\partial \zeta_1}&\cdots& \frac{\partial f_n(\xi^*,\zeta^*)}{\partial \zeta_m} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-02d8fb9441471b4730389431ccc6f27c_l3.png)
これから次の線形状態方程式を得ます。

したがって、次に留意します。
線形状態方程式の「零状態![]() 」は平衡状態
」は平衡状態![]() にあることを意味し、これは平衡入力
にあることを意味し、これは平衡入力![]() によってもたらされるので「零入力
によってもたらされるので「零入力![]() 」を前提とする。
」を前提とする。
●図9は非線形シミュレータ(非線形状態方程式)を用いて線形制御(状態フィードバック)の評価を行う場合の構成を、線形シミュレータ(線形状態方程式)を用いる場合と対比させています。
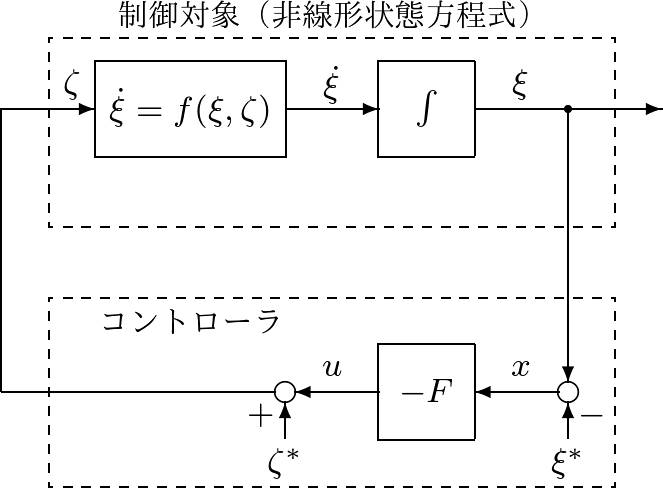
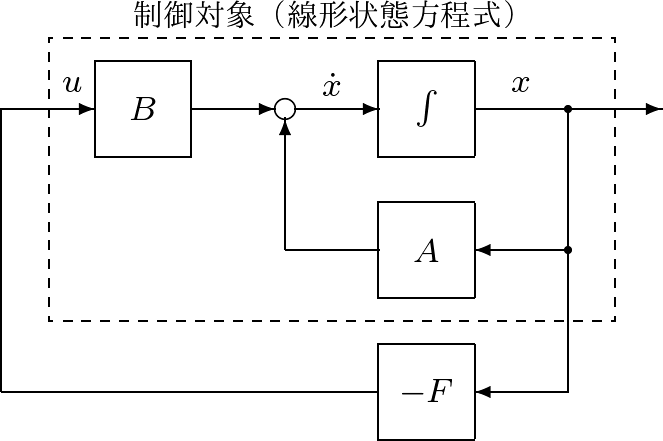
図9 非線形シミュレータと線形シミュレータの比較
演習A12-3…Flipped Classroom
非線形状態方程式(6)から線形状態方程式(7)を、次式を用いて示せ。
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{cc} \xi_1-\xi_1^* \\ \xi_2-\xi_2^* \end{array}\right] }_{\dot{x}=\dot{\xi}-\dot{\xi}^*}= \underbrace{ \left[\begin{array}{cc} \frac{\partial f_1(\xi^*,\tau^*)}{\partial \xi_1} & \frac{\partial f_1(\xi^*,\tau^*)}{\partial \xi_2} \\ \frac{\partial f_2(\xi^*,\tau^*)}{\partial \xi_1} & \frac{\partial f_2(\xi^*,\tau^*)}{\partial \xi_2} \end{array}\right] }_{A=\frac{\partial f(\xi^*,\tau^*)}{\partial \xi}} \underbrace{ \left[\begin{array}{l} \xi_1-\xi_1^* \\ \xi_2-\xi_2^* \end{array}\right] }_{x=\xi-\xi^*} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f2c5af558fdbb6c9d48962d44eed85a8_l3.png)
●制御対象が![]() 自由度をもつ力学系の場合、運動方程式の一般式は
自由度をもつ力学系の場合、運動方程式の一般式は
![]()
で与えられます(![]() は
は![]() 個の位置変数からなるベクトル、
個の位置変数からなるベクトル、![]() は
は![]() 個の速度変数からなるベクトル)。このとき非線形状態方程式は次式となります。
個の速度変数からなるベクトル)。このとき非線形状態方程式は次式となります。
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \underbrace{\frac{d}{dt} \left[\begin{array}{l} \xi_1 \\ \xi_2 \end{array}\right]}_{\dot{\xi}} =\underbrace{ \left[\begin{array}{l} \xi_2 \\ M^{-1}(\xi_1)(\zeta-C(\xi_1,\xi_2)\xi_2-G(\xi_1)) \end{array}\right]}_{f(\xi,\zeta)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5135df93ea761445ca840c16e381cc07_l3.png)
また平衡状態![]() と平衡入力
と平衡入力![]() は非線形連立方程式
は非線形連立方程式
![]()
を解いて求めます(fsolveの利用)。さらに線形化を行うと
![Rendered by QuickLaTeX.com \displaystyle{(24)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{cc} \xi_1-\xi_1^* \\ \xi_2-\xi_2^* \end{array}\right] }_{\dot{x}}= \underbrace{ \left[\begin{array}{cc} 0 & I_n \\ A_{21} & A_{22} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{l} \xi_1-\xi_1^* \\ \xi_2-\xi_2^* \end{array}\right] }_{x}+ \underbrace{ \left[\begin{array}{cc} 0 \\ B_2 \end{array}\right] }_{B} \underbrace{ (\zeta-\zeta^*) }_{u} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-367b63505bbc335acbc7077f5650a169_l3.png)
の形式となります。
Note A12 剛体振り子…Homework
一様な剛体の棒の一端を軸支した剛体振り子を考えます。この平衡状態はもちろん棒が鉛直線に沿っている状態ですが、回転軸が上端にある場合と下端にある場合とで2種類の平衡状態(![]() )と(
)と(![]() )をもつところが単振り子と違います。(
)をもつところが単振り子と違います。(![]() )の方は、人が1輪車に乗った状況を模擬しているといえます。
)の方は、人が1輪車に乗った状況を模擬しているといえます。
 図1 剛体振り子
図1 剛体振り子
いま回転軸回りの棒の運動を考えます。剛体の回転運動は「慣性モーメント×角加速度=トルク」で表されますので、棒の回転角を![]() とすると、運動方程式は次式となります。
とすると、運動方程式は次式となります。
![]()
ここで、![]() は棒の長さ、
は棒の長さ、![]() は棒の質量、
は棒の質量、![]() は重力加速度です。回転軸回りの慣性モーメント
は重力加速度です。回転軸回りの慣性モーメント![]() は、まず重心回りの慣性モーメント
は、まず重心回りの慣性モーメント
![]()
を求めて、平行軸の定理を使って、次のように計算されます(積分範囲を![]() から
から![]() としてもよい)。
としてもよい)。
![]()
結局、剛体振り子の運動を調べるためには、次の微分方程式を解くことになります。
![]()
一般に平衡状態が何らかの原因で乱されたとき、元の平衡状態に戻すことが制御動作と考えられます。したがって、剛体振り子の平衡状態近傍の運動の理解が大切となります。単振り子の場合に調べたように、平衡状態回りでは右辺を1次近似しても、元の解の振舞いをよく表していました。でも剛体振り子の場合は2種類の平衡状態があるので、少し注意が必要です。![]() の
の![]() における展開式
における展開式
![]()
を用いて、平衡状態(![]() )の近傍では(
)の近傍では(![]() )、
)、![]() として
として
![]()
また平衡状態(![]() )の近傍では(
)の近傍では(![]() )、
)、![]() として
として
![]()
のような1次近似を行います。これらに基づいてシミュレーションを行う場合は、それぞれ次式を用います。
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \underbrace{ \left[\begin{array}{l} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{3g}{4\ell}&0 \end{array}\right] }_{A_\alpha} \underbrace{ \left[\begin{array}{l} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aab7f16339e56d265534f36b3b8a9366_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{l} \theta(t)-\pi \\ \omega(t)-0 \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ \frac{3g}{4\ell}&0 \end{array}\right] }_{A_\beta} \underbrace{ \left[\begin{array}{l} \theta(t)-\pi \\ \omega(t)-0 \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-89b5ecb0d715edc56311f92b25c00853_l3.png)
これらの線形状態方程式(8),(9)は、非線形状態方程式(4)を、線形化して得られます。
最後に、長さ![]() をもつ剛体振り子と同じ周期をもつ単振り子の長さ
をもつ剛体振り子と同じ周期をもつ単振り子の長さ![]() を求めておきます。これは撃力中心の位置を表しています。これは振れ止めの制御を行う場合、重要な役割を果たします。
を求めておきます。これは撃力中心の位置を表しています。これは振れ止めの制御を行う場合、重要な役割を果たします。
![]()
 図2 剛体振り子と同じ周期をもつ単振り子の長さは?
図2 剛体振り子と同じ周期をもつ単振り子の長さは?