線形系の状態空間表現

投稿日時: 投稿者:

線形系の状態空間表現…Homework

[1] 　制御対象は一般には非線形系ですが、ここでは重ね合わせの原理の成り立つ線形系（linear system）を考えます。制御対象のモデルとして、次の状態空間表現が用いられます。

\displaystyle{(1)\quad \boxed{\left\{\begin{array}{ll} \dot{x}(t)=Ax(t)+Bu(t)&(x(t)\in{\bf R}^n,u(t)\in{\bf R}^m)\\ y(t)=Cx(t)&(y(t)\in{\bf R}^p) \end{array}\right.} }

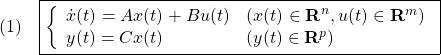
第１式は状態方程式とよばれ、x(t),u(t)はそれぞれ時刻tにおけるｎ個の状態変数、ｍ個の入力変数（アクチュエータを操作する）からなるベクトルを表しています。また、第２式は出力方程式とよばれ、y(t)は時刻tにおけるｐ個の出力変数（センサを用いて観測される）からなるベクトルを表しています。以下では状態空間表現(1)を簡単にn次系と参照します。

この状態空間表現は図1のようなブロック線図で表されます。

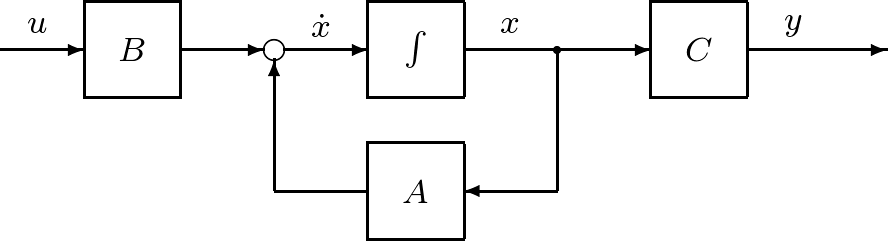図1 状態空間表現(1)のブロック線図

[2]　具体例を示すために、次図に示すマス・バネ・ダンパからなる機械系を考えます。これは直動型の緩衝装置を付けたドアを手動で開ける場合をモデル化したものです。

図2 マス・バネ・ダンパからなる機械系

状態空間表現を得るための出発点は，ニュートンの運動第２法則

\displaystyle{(2)\quad M\ddot{r}(t)=F(t) }

です。ここで，Mはドアの質量，r(t)は時刻tにおけるドアの変位，F(t)は時刻tにおいてドアに働く力であり

\displaystyle{(3)\quad F(t)=-D\dot{r}(t)-Kr(t)+u(t) }

のように表すことができます。ここで，ダンパが第1項の力を，ばねが第2項の力を与えます。uは人がドアに与える力とします。

\displaystyle{(4)\quad M\ddot{r}(t)=-D\dot{r}(t)-Kr(t)+u(t) }

これは2階の線形微分方程式ですが，v(t)=\dot{r}(t)を定義すると

\displaystyle{(5)\quad \left\{\begin{array}{l} \dot{r}(t)=v(t) \\ \dot{v}(t)=-\frac{D}{M}v(t)-\frac{K}{M}r(t)+\frac{1}{M}u(t) \end{array}\right. }

のような1階の連立線形微分方程式で表されます。これらを行列表示すると

\displaystyle{(6)\quad \underbrace{ \left[\begin{array}{c} \dot{r}(t) \\ \dot{v}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{K}{M} & -\frac{D}{M} \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} r(t) \\ v(t) \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{c} 0 \\ \frac{1}{M} \end{array}\right] }_B u(t) }

のような状態方程式を得ます。ドアが閉まっている場合の状態と入力は、次のように零状態と零入力として与えられます。

\displaystyle{(7)\quad x^*= \left[\begin{array}{c} 0 \\ 0 \end{array}\right],\ u^*=0 }

一方、センサを用いて観測される変数を位置とするとき、これを状態の線形関数として表して、次の出力方程式を得ます。

\displaystyle{(8)\quad \underbrace{r(t)}_{y(t)}= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} r(t) \\ v(t) \end{array}\right] }_{x(t)} }

演習A11…Flipped Classroom

次図のような連結台車を考えます。


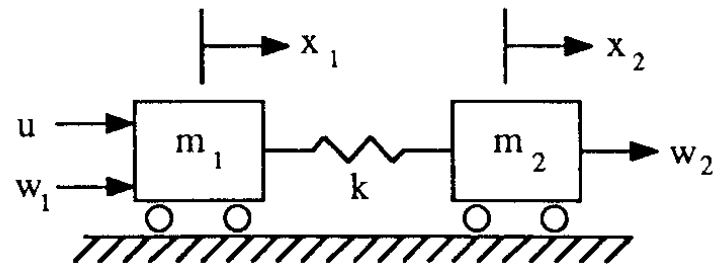
図3 連結台車(ACCベンチマーク問題)

これは次の運動方程式で表されます。

\displaystyle{(9)\quad \left\{\begin{array}{l} m_1\ddot{x}_1(t)=k(x_2(t)-x_1(t))+u(t)+w_1(t)\\ m_2\ddot{x}_2(t)=k(x_1(t)-x_2(t))+w_2(t) \end{array}\right. }

このとき、次の状態方程式を求めよ。

\displaystyle{(10)\quad \frac{d}{dt}\left[\begin{array}{c} x_1\\ x_2\\ \dot{x}_1\\ \dot{x}_2 \end{array}\right] = \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{array}\right] \left[\begin{array}{c} x_1\\ x_2\\ \dot{x}_1\\ \dot{x}_2 \end{array}\right] + \left[\begin{array}{ccc} 0 & 0 & 0\\ 0 & 0 & 0\\ b_{31} & b_{32} & b_{33}\\ b_{41} & b_{42} & b_{43} \end{array}\right] \left[\begin{array}{c} u\\ w_1\\ w_2 \end{array}\right] }

Note A11-1　代表的な状態方程式　

代表的な１次系の状態方程式は次式で表されます。

\displaystyle{(1)\quad \boxed{\dot{x}(t)=\underbrace{-\frac{1}{T}}_{a}x(t)+\underbrace{\frac{K}{T}}_{b}u(t)}}

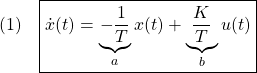
代表的な２次系の状態方程式は次式で表されます。

\displaystyle{(2)\quad \boxed{ \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] }_{\dot x} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{c} 0 \\ K\omega_n^2 \end{array}\right] }_{B} u(t) }}

これらをなぜこのようにパラメタライズするかはあとで述べます。

Note A11-2　直達項をもつ状態空間表現　

次のように直達項をもつ状態空間表現を考えることがあります。

\displaystyle{(1)\quad \boxed{\left\{\begin{array}{ll} \dot{x}(t)=Ax(t)+Bu(t)&(x(t)\in{\bf R}^n,u(t)\in{\bf R}^m)\\ y(t)=Cx(t)+Du(t)&(y(t)\in{\bf R}^p) \end{array}\right.} }

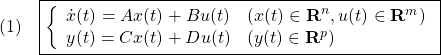
直達項は制御対象のモデルに対して用いられることは稀ですが、あとで述べるコントローラのモデルに対して用いられます（コントローラも状態空間表現として表すこと自体が驚きかもしれませんが）。

Note A11-3　直列結合　

次の２つの状態空間表現

\displaystyle{(1)\quad \left\{\begin{array}{l} \dot x_1(t)=A_1x_1(t)+B_1u_1(t) \\ y_1(t)=C_1x_1(t)+D_1u_1(t) \end{array}\right. }

\displaystyle{(2)\quad \left\{\begin{array}{l} \dot x_2(t)=A_2x_2(t)+B_2u_2(t) \\ y_2(t)=C_2x_2(t)+D_2u_2(t) \end{array}\right. }

に対して直列結合u_1=y_2を行うと、次の状態空間表現を得ます。

\displaystyle{(3)\quad \boxed{\left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right]= \left[\begin{array}{cc} A_1 & B_1C_2 \\ 0 & A_2 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + \left[\begin{array}{cc} B_1D_2 \\ B_2 \end{array}\right] u_2(t) \\ y_1(t)= \left[\begin{array}{cc} C_1 & D_1C_2 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] +D_1D_2u_2(t) \end{array}\right.} }

Note A11-4　座標変換　

状態空間表現

\displaystyle{(1)\quad \left\{\begin{array}{l} \dot x(t)=Ax(t)+Bu(t) \\ y(t)=Cx(t)+Du(t) \end{array}\right. }

における状態xを新しい状態x'に、正則行列Tを用いた

\displaystyle{(2)\quad x'(t)=Tx(t)\ \Leftrightarrow\ x(t)=T^{-1}x'(t) }

によって変換すると

\displaystyle{(3)\quad \left\{\begin{array}{l} T^{-1}\dot{x}'(t)=AT^{-1}x'(t)+Bu(t) \\ y(t)=CT^{-1}x'(t)+Du(t) \end{array}\right. }

すなわち

\displaystyle{(4)\quad \boxed{\left\{\begin{array}{l} \dot{x}'(t)=\underbrace{TAT^{-1}}_{A'}x'(t)+\underbrace{TB}_{B'}u(t) \\ y(t)=\underbrace{CT^{-1}}_{C'}x'(t)+Du(t) \end{array}\right.} }

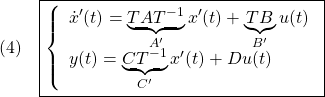
を得ます。