1次系の追値制御…Homework
[1] 定値外乱![]() をもつ1次系
をもつ1次系
![]()
を考えます。これに状態フィードバック
![]()
を行うと、閉ループ系は
![]()
となります。この時間応答は
![Rendered by QuickLaTeX.com (4)\quad \begin{array}{l} \displaystyle{x(t)=e^{(a-bf)t}x(0)+\int_0^t e^{(a-bf)(t-\tau)}w\,d\tau}\\ \displaystyle{=e^{(a-bf)t}x(0)+\left[\frac{1}{-(a-bf)}e^{(a-bf)(t-\tau)}w\right]_0^t}\\ \displaystyle{=e^{(a-bf)t}x(0)+\frac{w}{-(a-bf)}(1-e^{(a-bf)t})}\\ \displaystyle{\rightarrow \frac{w}{-(a-bf)}\ne 0 \quad (t\rightarrow\infty)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-87ff2adf2a1f8bd25d390b2196807faa_l3.png)
となり、平衡状態への復帰はできないことがわかります。そこで、フィードフォワード項をもつ状態フィードバック
![]()
を行うと、閉ループ系は
![]()
となり、この時間応答は
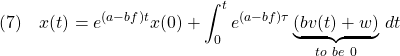
で表されます。ここで、フィードフォワード項を
![]()
と定めれば、定値外乱の影響を除去できます。しかしながら、ここでは外乱は一定であることはわかっているが、その値までは分からないと仮定して話を進めていきます。したがって、外乱の値![]() を推定する仕組みを工夫する必要があります。
を推定する仕組みを工夫する必要があります。
●いま、その仕組みとして、積分動作
![]()
を加えた状態フィードバック
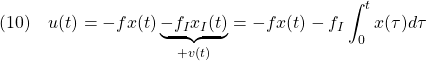
を考えます。これによる閉ループ系は
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad {\underbrace{ \left[\begin{array}{cc} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_E} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right] }_{A_{EF}} \underbrace{ \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{x_E} + \underbrace{ \left[\begin{array}{cc} w \\ 0 \end{array}\right] }_{w_E}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-31b2a3c2e865a17fd4319135d80cb684_l3.png)
となります。ここで、![]() の特性方程式は
の特性方程式は
![]()
ですが、その解が複素左半平面に含まれるように、![]() と
と![]() を適切に選んでおきます。
を適切に選んでおきます。
|
<このパートは最初は読み飛ばして結構です> このとき閉ループ系の時間応答は、
に注意して、次のように計算できます。
|
したがって、![]() のとき、次式が成り立ちます。
のとき、次式が成り立ちます。
![Rendered by QuickLaTeX.com (15)\quad \begin{array}{l} \displaystyle{\left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] \rightarrow - \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right]^{-1} \left[\begin{array}{cc} w \\ 0 \end{array}\right]}\\ \displaystyle{ = -\frac{1}{bf_I} \left[\begin{array}{cc} 0 & bf_I \\ -1 & a-bf \end{array}\right] \left[\begin{array}{cc} w \\ 0 \end{array}\right] = \left[\begin{array}{cc} 0 \\ \frac{1}{bf_I}w \end{array}\right]} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b2e96500c3db9199db1fbc40cbaa0029_l3.png)
![]()
すなわち、積分動作をもつ状態フィードバック(10)により、定値外乱の影響を受けずに、平衡状態に復帰できていることが確かめられます。
●定値外乱![]() をもつ1次系(1)に対して、制御目的
をもつ1次系(1)に対して、制御目的
![]()
を達成するために(![]() は目標値)、上述の積分動作を次のように変えてみます。
は目標値)、上述の積分動作を次のように変えてみます。
![]()
これを加えた状態フィードバック
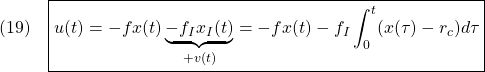
による閉ループ系は
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad \boxed{\underbrace{ \left[\begin{array}{cc} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_E} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right] }_{A_{EF}} \underbrace{ \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{x_E} + \underbrace{ \left[\begin{array}{cc} w \\ -r_c \end{array}\right] }_{w_E}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ddef16b35db1273870bc586e72b3bb5a_l3.png)
となるので、![]() のとき、次式が成り立ちます。
のとき、次式が成り立ちます。
![Rendered by QuickLaTeX.com \displaystyle{(21)\quad \begin{array}{l} \displaystyle{\left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] \rightarrow - \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right]^{-1} \left[\begin{array}{cc} w \\ -r_c \end{array}\right]}\\ \displaystyle{= -\frac{1}{bf_I} \left[\begin{array}{cc} 0 & bf_I \\ -1 & a-bf \end{array}\right] \left[\begin{array}{cc} w \\ -r_c \end{array}\right] = \left[\begin{array}{cc} r_c \\ \frac{1}{bf_I}w+\frac{a-bf}{bf_I}r_c \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f812ff0b7b34a62587cc56d0da3ad5fd_l3.png)
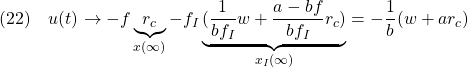
すなわち、積分動作をもつ状態フィードバック(19)により、定値外乱の影響を受けずに、制御目的(17)を達成できていることが確かめられます。
(21)から次式を得ます。
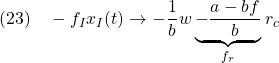
これから第2項![]() を、図2のように、フィードフォワードしておくことが考えられます。
を、図2のように、フィードフォワードしておくことが考えられます。
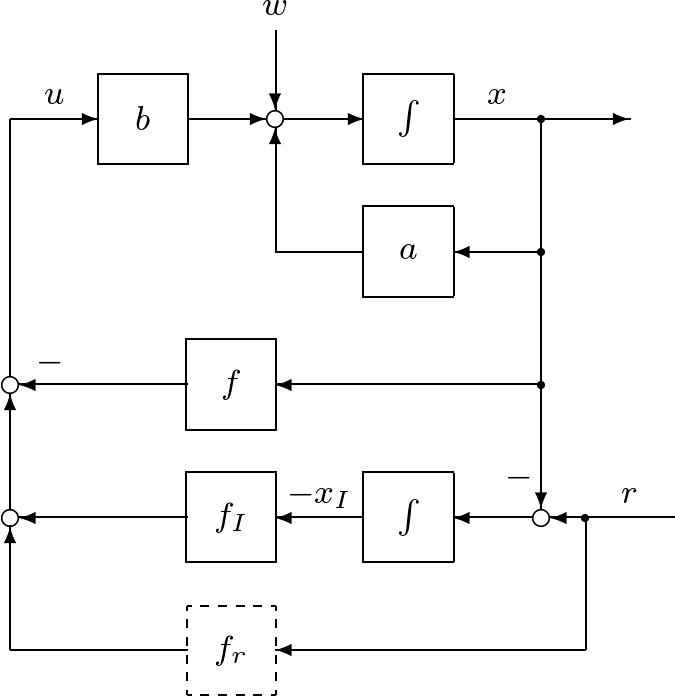
図1 積分動作を加えた状態フィードバックによる閉ループ系
●![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() として、次のシミュレーション結果を得ます。
として、次のシミュレーション結果を得ます。
 図2 図1のシミュレーション例
図2 図1のシミュレーション例
演習A04-1…Flipped Classroom
図2のグラフを描け。
| MATLAB |
|
| SCILAB |
|
[2] 定値外乱![]() をもつ1次系
をもつ1次系
![]()
に対して、制御目的
![]()
を達成するために(![]() は目標値)、積分動作
は目標値)、積分動作
![]()
を加えた状態フィードバック
![]()
を考えます。これは、実際には、状態オブザーバ
![]()
によって推定された状態![]() を用いて
を用いて
![]()
を実施することになります。この積分動作を加えたオブザーバベースコントローラは、(29)を(28)に代入した
![]()
と、(26)を合わせて、つぎのように表されます。
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \boxed{ \begin{array}{l} \left[\begin{array}{c} \dot{\hat{x}}(t) \\ \dot{x}_I(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} a-hc-bf & -bf_I \\ 0 & 0 \end{array}\right] }_{A_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right] + \underbrace{ \left[\begin{array}{cc} h & 0\\ 1 & -1 \end{array}\right] }_{B_K} \left[\begin{array}{c} y(t) \\ r_c \end{array}\right]\\ u(t)= \underbrace{- \left[\begin{array}{cc} f & f_I \end{array}\right] }_{C_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c9a64fdc6b3c7ee88c4b4ccbe8c58b7b_l3.png)
これによる閉ループ系は、(27)を(24)に代入した
![]()
と、(26)、(30)を合わせて
![Rendered by QuickLaTeX.com \displaystyle{(33)\quad \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\ \dot{\hat{x}}(t) \end{array}\right] = \left[\begin{array}{ccc} a & -bf_I & -bf \\ c & 0 & 0 \\ hc & -bf_I & a-hc-bf \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r_c \\ 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ec175798327a5fc11b68b91a22172f0d_l3.png)
のように表されます。そのブロック線図を図3に示します。
いま、閉ループ系(33)に、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(34)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\ e(t) \end{array}\right] = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -1 & 0 & 1 \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7ca97b463935b7f71dea225ffcb573f2_l3.png)
を行えば
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad \boxed{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\\hline \dot{e}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} a-bf & -bf_I & -bf \\ c & 0 & 0 \\\hline 0 & 0 & a-hc \end{array}\right] }_{ A_{EF}'= \left[\begin{array}{c|c} A_{EF} & - \left[\begin{array}{cc} bf \\ 0 \end{array}\right] \\[5mm] \hline 0 & \widehat{a} \end{array}\right] } \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r_c \\\hline -w \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3a0c12a07d48d608c414bfef747b7ae3_l3.png)
となります。オブザーバの誤差方程式が分離されており、![]() と
と![]() を独立に設計してもよいことが分かります。
を独立に設計してもよいことが分かります。
ここで、![]() の特性方程式の解は左半平面にあるとすると、(35)より、
の特性方程式の解は左半平面にあるとすると、(35)より、![]() のとき、次式が成り立ちます。
のとき、次式が成り立ちます。
![Rendered by QuickLaTeX.com \displaystyle{(36)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] \ \rightarrow\ \underbrace{ \left[\begin{array}{c|c} A_{EF}^{-1} & -A_{EF}^{-1} \left[\begin{array}{cc} bf \\ 0 \end{array}\right] \widehat{a}^{-1} \\[5mm]\hline 0 & \widehat{a}^{-1} \end{array}\right] }_{A_{EF}'\,^{-1}} \left[\begin{array}{c} -w \\ r_c \\\hline w \end{array}\right] \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c8709893951656a10a2cf0aec18bef8b_l3.png)
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad \begin{array}{l} \displaystyle{\left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] \rightarrow \left[\begin{array}{cc} a-bf & -bf_I \\ c & 0 \end{array}\right]^{-1} \left[\begin{array}{cc} -w-bf\widehat{a}^{-1}w\\ r_c \end{array}\right]}\\ \displaystyle{= \frac{1}{cbf_I} \left[\begin{array}{cc} 0 & bf_I \\ -c & a-bf \end{array}\right] \left[\begin{array}{cc} -w-bf\widehat{a}^{-1}w\\ r_c \end{array}\right]}\\ \displaystyle{= \left[\begin{array}{cc} \frac{1}{c}r_c \\ \frac{1}{bf_I}w+\frac{1}{f_I}f\widehat{a}^{-1}w+\frac{a-bf}{cbf_I}r_c \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a0408f31040df6a4e4b055bc9c88bc05_l3.png)
![]()
したがって
![]()
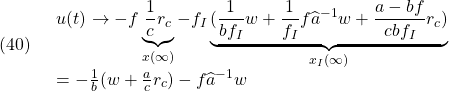
を得ます。したがって、定値外乱が存在するときは状態オブザーバに関して定常偏差が残るにもかかわらず、制御目的(24)が成り立つことがわかります。
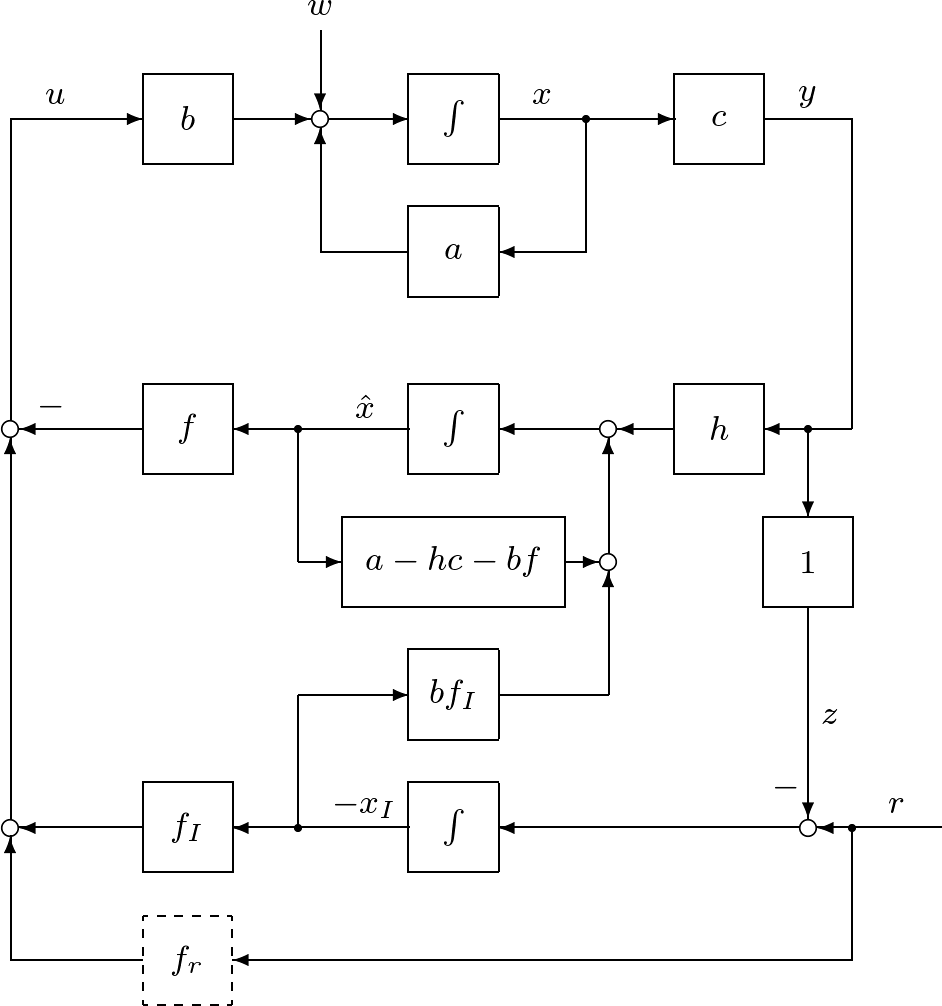 図3 積分動作を加えたオブザーバベースコントローラによる閉ループ系
図3 積分動作を加えたオブザーバベースコントローラによる閉ループ系
1次系のLQI制御…Homework
[3] 定値外乱![]() をもつ1次系(23)に対して、制御目的(24)を達成するための制御則として、積分動作(25)をもつ安定化状態フィードバック(26)を考えます。これによる閉ループ系
をもつ1次系(23)に対して、制御目的(24)を達成するための制御則として、積分動作(25)をもつ安定化状態フィードバック(26)を考えます。これによる閉ループ系
![Rendered by QuickLaTeX.com \displaystyle{(41)\quad \underbrace{ \left[\begin{array}{cc} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ c & 0 \end{array}\right] }_{A_{EF}} \underbrace{ \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{x_E(t)} + \underbrace{ \left[\begin{array}{cc} w \\ -r_c \end{array}\right] }_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f729fc6c953923d57572c53768579876_l3.png)
に対して、評価関数
![]()
を最小化するように ![]() と
と![]() を決めるLQI制御問題を考えます。いま、出力方程式
を決めるLQI制御問題を考えます。いま、出力方程式
![Rendered by QuickLaTeX.com \displaystyle{(43)\quad \underbrace{ \left[\begin{array}{cc} qx(t)\\ ru(t) \end{array}\right] }_{y_{E}(t)} = \underbrace{ \left[\begin{array}{cc} q & 0 \\ -rf & -rf_I \end{array}\right] }_{C_{E}} \underbrace{ \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{x_{E}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0d18a388e7b6c8f9fa04453e84d71145_l3.png)
を定義すると、閉ループ系の応答は
|
<このパートは最初は読み飛ばして結構です> より
|
となります。ここで、第2項の定数項があるので、評価関数
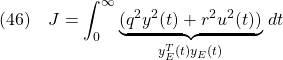
は発散してしまいます(そもそも外乱は未知としますので計算もできません)。
●そこで、定値外乱が抑制されているときは、平衡状態(![]() )は
)は![]() に、平衡入力(
に、平衡入力(![]() )は
)は![]() に変わっていることに注意し、これとの差を表す状態方程式を考えます。まず定値外乱抑制前の状態方程式は(1)と(2)を合わせて
に変わっていることに注意し、これとの差を表す状態方程式を考えます。まず定値外乱抑制前の状態方程式は(1)と(2)を合わせて
![Rendered by QuickLaTeX.com \displaystyle{(47)\quad \underbrace{\frac{d}{dt} \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} a & 0 \\ c & 0 \end{array}\right] }_{A_E} \underbrace{ \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{x_E(t)} + \underbrace{ \left[\begin{array}{cc} b \\ 0 \end{array}\right] }_{B_E} u(t) + \underbrace{ \left[\begin{array}{cc} w \\ -r_c \end{array}\right] }_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4e152ba9118c145fdc3aa9097ad1291f_l3.png)
となります。また、定値外乱抑制後には
![Rendered by QuickLaTeX.com \displaystyle{(48)\quad \underbrace{\frac{d}{dt} \left[\begin{array}{cc} x_\infty \\ x_{I\infty} \end{array}\right] }_{\dot{x}_{E\infty}=0} = \underbrace{ \left[\begin{array}{cc} a & 0 \\ c & 0 \end{array}\right] }_{A_E} \underbrace{ \left[\begin{array}{cc} x_\infty \\ x_{I\infty} \end{array}\right] }_{x_{E\infty}} + \underbrace{ \left[\begin{array}{cc} b \\ 0 \end{array}\right] }_{B_E} u_\infty + \underbrace{ \left[\begin{array}{cc} w \\ -r_c \end{array}\right] }_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-388e3b63a548f6ae3de1bca82350d6b8_l3.png)
が成り立ちます。両者を辺々引き算して
![Rendered by QuickLaTeX.com \displaystyle{(49)\quad \boxed{ \underbrace{\frac{d}{dt} \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{\dot{x}_{E1}(t)} = \underbrace{ \left[\begin{array}{cc} a & 0 \\ c & 0 \end{array}\right] }_{A_{E1}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{x_{E1}(t)} + \underbrace{ \left[\begin{array}{cc} b \\ 0 \end{array}\right] }_{B_{E1}} \underbrace{(u(t)-u_\infty)}_{u_{E1}(t)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ef61060eeffd371eb2eb609612504541_l3.png)
となります。これを偏差系E1と呼ぶことにします。これに安定化状態フィードバック
![Rendered by QuickLaTeX.com \displaystyle{(50)\quad \underbrace{u(t)-u_\infty}_{u_{E1}(t)} =- \underbrace{ \left[\begin{array}{cc} f & f_I \end{array}\right] }_{F_E} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{x_{E1}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2de715ba671f8a4ff5fe87b581f7486f_l3.png)
を行った閉ループ系は
![Rendered by QuickLaTeX.com \displaystyle{(51)\quad \underbrace{\frac{d}{dt} \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{\dot{x}_{E1}(t)} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ c & 0 \end{array}\right] }_{A_{EF}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{x_{E1}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0ac4b58fae5895656374987e2e2dfb53_l3.png)
となります。いま出力方程式
![Rendered by QuickLaTeX.com \displaystyle{(52)\quad \underbrace{ \left[\begin{array}{cc} q(x(t)-x_\infty) \\ r(u(t)-u_\infty) \end{array}\right] }_{y_{E1}(t)} = \underbrace{ \left[\begin{array}{cc} q & 0 \\ -rf & -rf_I \end{array}\right] }_{C_{E1}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{x_{E1}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f6ff94e985ffd90ab5da603d6e28d94f_l3.png)
を定義して、評価関数
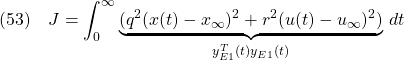
を最小化して、(50)のフィードバックゲイン![]() と
と![]() を決める制御方式を偏差系E1に基づくLQI制御と呼びます。
を決める制御方式を偏差系E1に基づくLQI制御と呼びます。
●さて、偏差系E1すなわち(49)の両辺を微分すると2つめの偏差系E2
![Rendered by QuickLaTeX.com \displaystyle{(54)\quad \boxed{ \underbrace{\frac{d}{dt} \left[\begin{array}{cc} \dot{x}(t) \\ x(t)-r_c \end{array}\right] }_{\dot{x}_{E2}(t)} = \underbrace{ \left[\begin{array}{cc} a & 0 \\ c & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} \dot{x}(t) \\ x(t)-r_c \end{array}\right] }_{x_{E2}(t)} + \underbrace{ \left[\begin{array}{cc} b \\ 0 \end{array}\right] }_{B_{E2}} \underbrace{\dot{u}(t)}_{u_{E2}(t)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d55bc528b4211e44104d9a016f1efe77_l3.png)
を得ます。また(49)は次のように変形できることに注意します。
![Rendered by QuickLaTeX.com \displaystyle{(55)\quad \left[\begin{array}{cc} \dot{x}(t) \\ x(t)-r_c \end{array}\right] = \underbrace{ \left[\begin{array}{cc} a & b \\ c & 0 \end{array}\right] }_{S} \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b36ebc36ec3a8aa2b181e54a374490a4_l3.png)
これを(15)に代入すると
![Rendered by QuickLaTeX.com (56)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} a & b \\ c & 0 \end{array}\right] }_{S} \frac{d}{dt} \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]=\\ \underbrace{ \left[\begin{array}{cc} a & 0 \\ 1 & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} a & b \\ c & 0 \end{array}\right] }_{S} \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] + \underbrace{ \left[\begin{array}{cc} b \\ 0 \end{array}\right] }_{B_{E2}} \underbrace{\dot{u}(t)}_{u_{E2}(t)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3fe9bb9955ebd8e2c8e93bbd706c8fe9_l3.png)
この左から![]() をかけると3つめの偏差系E3
をかけると3つめの偏差系E3
![Rendered by QuickLaTeX.com \displaystyle{(57)\quad \boxed{\underbrace{ \frac{d}{dt} \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}} = \underbrace{ \left[\begin{array}{cc} a & b \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}} + \underbrace{ \left[\begin{array}{cc} 0 \\ 1 \end{array}\right] }_{B_{E3}} \underbrace{\dot{u}(t)}_{u_{E3}(t)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c85ae085cc84c481ab12fad21f3f8ae0_l3.png)
を得ます。これに安定化状態フィードバック
![Rendered by QuickLaTeX.com \displaystyle{(58)\quad \underbrace{\dot{u}(t)}_{u_{E3}(t)} =- \underbrace{ \left[\begin{array}{cc} k & k_I \end{array}\right] }_{K_E} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b8ffb28df7a25dd49c60692720881d34_l3.png)
を行った閉ループ系は
![Rendered by QuickLaTeX.com \displaystyle{(59)\quad \underbrace{\frac{d}{dt} \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} a & b \\ -k & -k_I \end{array}\right] }_{A_{EK}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-150f484db41dfcfd7bc2713f40cf1398_l3.png)
となります。いま出力方程式
![Rendered by QuickLaTeX.com \displaystyle{(60)\quad \underbrace{ \left[\begin{array}{cc} q(x(t)-x_\infty) \\ r\dot{u}(t) \end{array}\right] }_{y_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} q & 0 \\ 0 & r\frac{d}{dt} \end{array}\right] }_{C_{E3}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-36376901e37df555679c68adbb340194_l3.png)
を定義して、評価関数
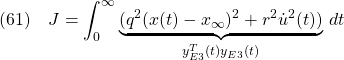
を最小化して、(59)のフィードバックゲイン![]() と
と![]() を決めます。(55)を(59)に代入して
を決めます。(55)を(59)に代入して
![Rendered by QuickLaTeX.com \displaystyle{(62)\quad \dot{u}(t) =- \underbrace{ \left[\begin{array}{cc} k & k_I \end{array}\right] }_{K_E} \underbrace{ \left[\begin{array}{cc} a & b \\ 1 & 0 \end{array}\right]^{-1} }_{S^{-1}} \left[\begin{array}{cc} \dot{x}(t) \\ x(t)-r_c \end{array}\right] =- \underbrace{ \left[\begin{array}{cc} f & f_I \end{array}\right] }_{F_E=K_ES^{-1}} \left[\begin{array}{cc} \dot{x}(t) \\ x(t)-r_c \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-84e71c3cc59f8a7feeedd162fdda01c6_l3.png)
これを積分して
![]()
を得ます。このようにして(3)のフィードバックゲイン![]() と
と![]() を決める制御方式を偏差系E3に基づくLQI制御と呼びます。
を決める制御方式を偏差系E3に基づくLQI制御と呼びます。
[4] 以下に、偏差系E3をLQG制御により安定化して、積分動作を加えたオブザーバベース コントローラを構成する手順を示します。
|
アルゴリズム <1次系のLQGI制御>
入力パラメータ ステップ1: 偏差系の安定化 偏差系
を、状態フィードバック
によるLQ制御で安定化します。その際、評価関数としては
を用いる。さらに、
ステップ2: オブザーバゲイン
を解いて,
ステップ3: 積分動作を加えたオブザーバベース コントローラの構成
ただし
|
この積分動作を加えたオブザーバベースコントローラによる制御方式をLQGI制御(LQG control with integral action)と呼びます。
![Rendered by QuickLaTeX.com (14)\quad \begin{array}{l} \displaystyle{x_E(t)=\exp(A_{EF}t)x_E(0)+\int_0^t\exp(A_{EF}(t-\tau))w_E\,d\tau}\\ \displaystyle{=\exp(A_{EF}t)x_E(0)+\left[-\exp(A_{EF}(t-\tau))A_{EF}^{-1}w_E\right]_0^t}\\ \displaystyle{=\exp(A_{EF}t)x_E(0)-(I_2-\exp(A_{EF}t))A_{EF}^{-1}w_E}\\ \displaystyle{=\exp(A_{EF}t)(x_E(0)+A_{EF}^{-1}w_E)-A_{EF}^{-1}w_E}\\ \displaystyle{\rightarrow -A_{EF}^{-1}w_E \quad (t\rightarrow\infty)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3bca83642ec9ba9f633fe5e502d53148_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(64)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} a & b \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c41509ad03419a701e8ac16d5e5fdd9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(70)\quad \begin{array}{l} \dot{x}_K(t)=A_Kx_K(t)+B_K \left[\begin{array}{c} y(t) \\ r_c \end{array}\right]\\ u(t)=C_Kx_K(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a49a6c693b0b6603def7809f250eda5e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(71)\quad \begin{array}{l} A_K= \left[\begin{array}{cc} a-hc-bf & -bf_I \\ 0 & 0 \end{array}\right]\\ B_K= \left[\begin{array}{cc} h & 0\\ 1 & -1 \end{array}\right]\\ C_K=- \left[\begin{array}{cc} f & f_I \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-78a0c63e2aa625650bb1f5593550221b_l3.png)