●パイプ(固定・質点付自由)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
●ワイヤ(ピン・質点付自由)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
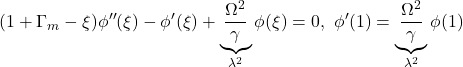
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
function y=freqeq(x)
s0=2*x*sqrt(1+gamma);
s1=2*x*sqrt(gamma);
y=besselj(0,s0).*(2*bessely(1,s1)-s1.*bessely(0,s1))…
-bessely(0,s0).*(2*besselj(1,s1)-s1.*besselj(0,s1));
endfunction
x=linspace(0.01,10,1000)’;
clf(0);scf(0);plot(x,freqeq(x)),mtlb_grid,mtlb_axis([0 10 -0.1 0.1])
w=locate(3);
lambda=[];
for i=1:3
x=fsolve(w(1,i),freqeq); lambda=[lambda x];
end
freqeq(lambda)
//—–
for i=1:3
x=lambda(i);
s0=2*x*sqrt(1+gamma);
s1=2*x*sqrt(gamma);
M=[besselj(0,s0) bessely(0,s0);
2*besselj(1,s1)-s1*besselj(0,s1) 2*bessely(1,s1)-s1*bessely(0,s1)];
[U,S,V]=svd(M);
c1(i)=V(1,2);
c2(i)=V(2,2);
end
function y=phi(i,x)
s=2*lambda(i).*sqrt(1+gamma-x);
y=c1(i)*besselj(0,s)+c2(i)*bessely(0,s);
endfunction
xi=(0.01:0.01:1)’;
y1=phi(1,xi);
y2=phi(2,xi);
y3=phi(3,xi);
clf(1);scf(1);plot(xi,y1,xi,y2,xi,y3),mtlb_grid
