行列指数関数 | 制御系CAD

定義

● $n$ 次正方行列 $X$ の行列指数関数
$\displaystyle{ \exp(X)=I_n+X+\frac{1}{2}X^2+\cdots+\frac{1}{k!}X^k+\cdots }$

●諸性質
$\displaystyle{1^{\circ}\ \exp(0)=I_n}$
$\displaystyle{2^{\circ}\ (\exp(X))^T=\exp(X^T)}$
$\displaystyle{3^{\circ}\ X=V\Lambda V^{-1}\ \Rightarrow \ \exp(X)=V\exp(\Lambda)V^{-1}}$
$\displaystyle{4^{\circ}\ XY=YX\ \Rightarrow \ \exp(X+Y)=\exp(X)\exp(Y)}$
$\displaystyle{5^{\circ}\ (\exp(X))^{-1}=\exp(-X)}$
$\displaystyle{6^{\circ}\ \frac{d}{dt}\exp(At)=A\exp(At)=\exp(At)A }$
$\displaystyle{7^{\circ}\ \det A\ne 0\ \Rightarrow \ \int \exp(At) dt=A^{-1}\exp(At)=\exp(At)A^{-1} }$

$1^\circ$ と $2^\circ$ は自明でしょう。

$3^\circ$ は一般項が次式となるためです。

$\displaystyle{\frac{1}{k!}X^k=\frac{1}{k!}(V\Lambda V^{-1})^k=\frac{1}{k!}V\Lambda^kV^{-1}}$

注意すべきは、 $4^\circ$ で、指数法則は可換な行列に対してのみ成立することです。これは

$\displaystyle{{\rm RHS}=(I_n+X+\frac{1}{2}X^2+\cdots)(I_n+Y+\frac{1}{2}Y^2+\cdots)}$
$\displaystyle{=I_n+X+Y+\frac{1}{2}X^2+XY+\frac{1}{2}Y^2+\cdots}$
$\displaystyle{=I_n+X+Y+\frac{1}{2}(X^2+2XY+Y^2)+\cdots}$

が

$\displaystyle{I_n+X+Y+\frac{1}{2}(X^2+XY+YX+Y^2)+\cdots}$
$\displaystyle{=I_n+X+Y+\frac{1}{2}(X+Y)^2+\cdots={\rm LHS}}$

と等しくなるためには $X$ と $Y$ が可換（ $XY=YX$ ）でなければならないからです。

$5^\circ$ は $4^\circ$ で $Y=-X$ とおけば出ます。

$6^\circ$ は一般項が

$\displaystyle{\frac{d}{dt}\frac{1}{k!}(At)^k=A\frac{1}{(k-1)!}(At)^{k-1}=\frac{1}{(k-1)!}(At)^{k-1}A}$

となることから出ます。

$7^\circ$ は $6^\circ$ の両辺を積分して

$\displaystyle{\exp(At)=A\int\exp(At)dt=\int\exp(At)dtA }$

となることから出ます。

２次の行列指数関数

● $n=2$ の場合、 $A$ の実Jordan標準形 $\Lambda$ は次の３つに分類されます。

$\displaystyle{1^{\circ}\ \lambda(A)=\{\lambda_1,\lambda_2\} \ \Rightarrow\ \Lambda_1=\left[\begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \end{array}\right]}$
$\displaystyle{2^{\circ}\ \lambda(A)=\{\lambda_R\pm j\lambda_I\} \ \Rightarrow\ \Lambda_2=\left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right]}$
$\displaystyle{3^{\circ}\ \lambda(A)=\{\lambda,\lambda\} \ \Rightarrow\ \Lambda_3=\left[\begin{array}{cc} \lambda & 1 \\ 0 & \lambda \end{array}\right]}$

このときの行列指数関数は次式で与えられます。

$\displaystyle{1^{\circ}\quad \exp(\Lambda_1 t)= \left[\begin{array}{cc} e^{\lambda_1t} & 0 \\ 0 & e^{\lambda_2 t} \end{array}\right] }$
$\displaystyle{2^{\circ}\quad \exp(\Lambda_2 t)=e^{\lambda_R t} \left[\begin{array}{cc} \cos(\lambda_It) & \sin(\lambda_It) \\ -\sin(\lambda_It) & \cos(\lambda_It) \end{array}\right] }$
$\displaystyle{3^{\circ}\quad \exp(\Lambda_3 t)=e^{\lambda t} \left[\begin{array}{cc} 1 & t \\ 0 & 1 \end{array}\right] }$

$2^\circ$ は、次式において、 $X$ と $Y$ が可換であることから出ます。

$\displaystyle{ \left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right]= \underbrace{\lambda_RI_2}_{X}+ \underbrace{\lambda_I \left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right]}_{Y} }$

$3^\circ$ は、次式において、 $X$ と $Y$ が可換であることから出ます。

$\displaystyle{ \left[\begin{array}{cc} \lambda & 1 \\ 0 & \lambda \end{array}\right]= \underbrace{\lambda I_2}_{X}+ \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right]}_{Y} }$

３次の行列指数関数

● $n=3$ の場合、 $A$ の実Jordan標準形 $\Lambda$ は次の４つに分類されます。

$\displaystyle{1^{\circ}\ \lambda(A)=\{\lambda_1,\lambda_2,\lambda_3\} \ \Rightarrow\ \Lambda_1=\left[\begin{array}{ccc} \lambda_1 & 0 & 0\\ 0 & \lambda_2 & 0\\ 0 & 0 & \lambda_3 \end{array}\right]}$
$\displaystyle{2^{\circ}\ \lambda(A)=\{\lambda_R\pm j\lambda_I,\lambda\} \ \Rightarrow\ \Lambda_2=\left[\begin{array}{ccc} \lambda_R & \lambda_I & 0 \\ -\lambda_I & \lambda_R & 0 \\ 0 & 0 & \lambda \end{array}\right]}$
$\displaystyle{3^{\circ}\ \lambda(A)=\{\lambda,\lambda,\lambda\} \ \Rightarrow\ \Lambda_3=\left[\begin{array}{ccc} \lambda & 1 & 0\\ 0 & \lambda & 1\\ 0 & 0 & \lambda \end{array}\right]}$
$\displaystyle{4^{\circ}\ \lambda(A)=\{\lambda,\lambda,\lambda'\} \ \Rightarrow\ \Lambda_4=\left[\begin{array}{ccc} \lambda & 1 & 0\\ 0 & \lambda & 0\\ 0 & 0 & \lambda' \end{array}\right]}$

このときの行列指数関数は次式で与えられます。

$\displaystyle{1^{\circ}\quad \exp(\Lambda_1 t)= \left[\begin{array}{ccc} e^{\lambda_1t} & 0 & 0\\ 0 & e^{\lambda_2 t} & 0\\ 0 & 0 & e^{\lambda_3 t} \end{array}\right] }$
$\displaystyle{2^{\circ}\quad \exp(\Lambda_2 t)= \left[\begin{array}{ccc} e^{\lambda_R t}\cos(\lambda_It) & e^{\lambda_R t}\sin(\lambda_It) & 0\\ -e^{\lambda_R t}\sin(\lambda_It) & e^{\lambda_R t}\cos(\lambda_It) & 0\\ 0 & 0 & e^{\lambda t} \end{array}\right] }$
$\displaystyle{3^{\circ}\quad \exp(\Lambda_3 t)=e^{\lambda t} \left[\begin{array}{ccc} 1 & t & \frac{t^2}{2} \\ 0 & 1 & t \\ 0 & 0 & 1 \\ \end{array}\right] }$
$\displaystyle{4^{\circ}\quad \exp(\Lambda_4 t)= \left[\begin{array}{ccc} e^{\lambda t} & te^{\lambda t} & 0\\ 0 & e^{\lambda t} & 0\\ 0 & 0 & e^{\lambda t} \end{array}\right] }$

一般の行列指数関数

●一般の場合、 $A$ の実Jordan標準形 $\Lambda$ は

$\Lambda= {\rm diag}\{J(\lambda_1,m_1),\cdots,J(\lambda_p,m_p), K(\lambda_{R1},\lambda_{I1},\ell_1),\cdots,K(\lambda_{Rq},\lambda_{Iq},\ell_q)\}$
（ $m_1+\cdots+m_p+2(\ell_1+\cdots+\ell_q)=n$ ）

すなわち、次の２種類のジョルダン細胞のブロック対角行列となります（ $\lambda$ , $\lambda_R$ , $\lambda_I(\ne0)$ は実数）。

$\displaystyle{1^{\circ}\quad J(\lambda,m)= \left[\begin{array}{cccc} \lambda & 1 & & \\ & \lambda & \ddots & \\ & & \ddots & 1 \\ & & & \lambda \end{array}\right]\in{\bf R}^{m\times m} }$

$\displaystyle{2^{\circ}\quad K(\lambda_{R},\lambda_{I},\ell)= \left[\begin{array}{c|c|cc|c} \begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array} & \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} & & \\ \hline & \begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array} & \ddots & & \\ \hline & & & & \\ \hline & & & \ddots & \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \\ \hline & & & & \begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array} \end{array}\right]\in{\bf R}^{2\ell\times 2\ell} }$

このときの行列指数関数は次式で与えられます。

$\displaystyle{1^{\circ}\quad \exp(J(\lambda,m)t)=e^{\lambda t} \left[\begin{array}{ccccc} 1 & t & \frac{t^2}{2} & \cdots & \frac{t^{m-1}}{(m-1)!} \\ & 1 & t & \ddots & \vdots \\ & & 1 & \ddots & \frac{t^2}{2} \\ & & & \ddots & t \\ & & & & 1 \end{array}\right] }$

$\displaystyle{2^{\circ}\quad \exp(K(\lambda_{R},\lambda_{I},\ell)t)= \exp(J(\lambda_R,\ell)t) \bigotimes e^{\lambda_R t} \left[\begin{array}{cc} \cos\lambda_It & \sin\lambda_It \\ -\sin\lambda_It & \cos\lambda_It \end{array}\right] }$

$1^\circ$ は、次式において、 $X$ と $Y$ が可換であることから出ます。

$\displaystyle{ J(\lambda,m)= \underbrace{\lambda I_m}_{X}+ \underbrace{ \left[\begin{array}{cccc} 0 & 1 & & \\ & 0 & \ddots & \\ & & \ddots & 1 \\ & & & 0 \end{array}\right]}_{Y} }$

$2^\circ$ は、まず次式のような $X$ と $Y$ の和となります。

$\displaystyle{ K(\lambda_{R},\lambda_{I},\ell)= \underbrace{\left[\begin{array}{cccc} \lambda_R & 1 & & \\ & \lambda_R & \ddots & \\ & & \ddots & 1 \\ & & & \lambda_R \end{array}\right] \otimes I_2 }_{X}+ \underbrace{I_\ell\otimes \lambda_I \left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right] }_{Y} }$

ここでクロネッカ積に関する恒等式

$\displaystyle{\underbrace{(A\otimes B)}_X\underbrace{(C\otimes D)}_Y=AC\otimes BD}$

を用いると、 $A$ と $C$ が可換、 $B$ と $D$ が可換であれば、 $X$ と $Y$ は可換となります（ $2^\circ$ の場合、ＯＫです）。また、次式が成り立つことが知られています。

$\displaystyle{\exp(A\otimes I+I\otimes B)=\exp(A\otimes I)\exp(I\otimes B)=\exp(A)\otimes \exp(B)}$

高次系の漸近安定性

●行列指数関数を用いると、微分方程式

$\displaystyle{\underbrace{\frac{dx(t)}{dt}}_{\dot{x}(t)}=Ax(t)}$

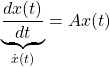
の解は次のように表されます。

$\displaystyle{x(t)=\exp(At)x(0)=V\exp(\Lambda t)V^{-1}x(0)}$

ここで

$\begin{array}{ll} &\exp(At)=V\exp(\Lambda t)V^{-1}={\displaystyle \sum_{i=1}^p\sum_{k=1}^{m_i}t^{k-1}}e^{\lambda_it}\,R_{ik} \\ &+{\displaystyle \sum_{i=1}^q\sum_{k=1}^{\ell_i}t^{k-1}}e^{\lambda_{Ri}t}\cos\lambda_{Ii}t\,C_{ik} +{\displaystyle \sum_{i=1}^q\sum_{k=1}^{\ell_i}t^{k-1}}e^{\lambda_{Ri}t}\sin\lambda_{Ii}t\,S_{ik} \end{array}$

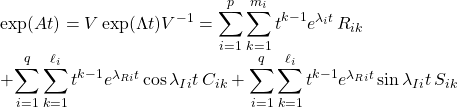
と書けることに注意します（ $R_{ik},C_{ik},S_{ik}$ は適当な $n$ 次実正方行列）。

したがって、任意の $x(0)\ne0$ に対して、 $t\rightarrow\infty$ のとき $x(t)\rightarrow 0$ となるための条件は

$\displaystyle{\exp(\Lambda t)\rightarrow 0\quad(t\rightarrow\infty)}$

となります。これは $A$ のすべての固有値の実部が負を意味します。

● $\dot{x}(t)=ax(t)$ （ $a=1,0,0.5$ ）の解のグラフを見ると、 $a=0$ の場合は、漸近安定ではないが、発散はしないので、不安定とまではいえないのではないかと思うかもしれません。したがって零の固有値を不安定とみなすのか、安定とみなすか迷うところです。しかし、 $\dot{x}(t)=Ax(t)$ において、 $A=\left[\begin{array}{cc} 0& 1\\ 0& 0 \end{array}\right]$ の場合、解は $x(t)=\left[\begin{array}{cc} 1& t\\ 0& 1 \end{array}\right]x(0)$ となって、 $x(0)$ の第２要素が零でない場合は発散します。したがって、一般には零の固有値は不安定とみなします。