●Drone becomes to be very popular tool to take a video from the sky. It is a surprise that we can control its motion with 6 degrees of freedom so smartly. What makes it possible?

In general, a drone has 4 propellers as shown. This means that 4 degrees of freedom can be controlled. They should be the heave ![]() and the roll
and the roll ![]() , the pitch
, the pitch ![]() , the yaw
, the yaw ![]() . Assume that rotational speeds of 4 propellers can be set to the specified values,
. Assume that rotational speeds of 4 propellers can be set to the specified values, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
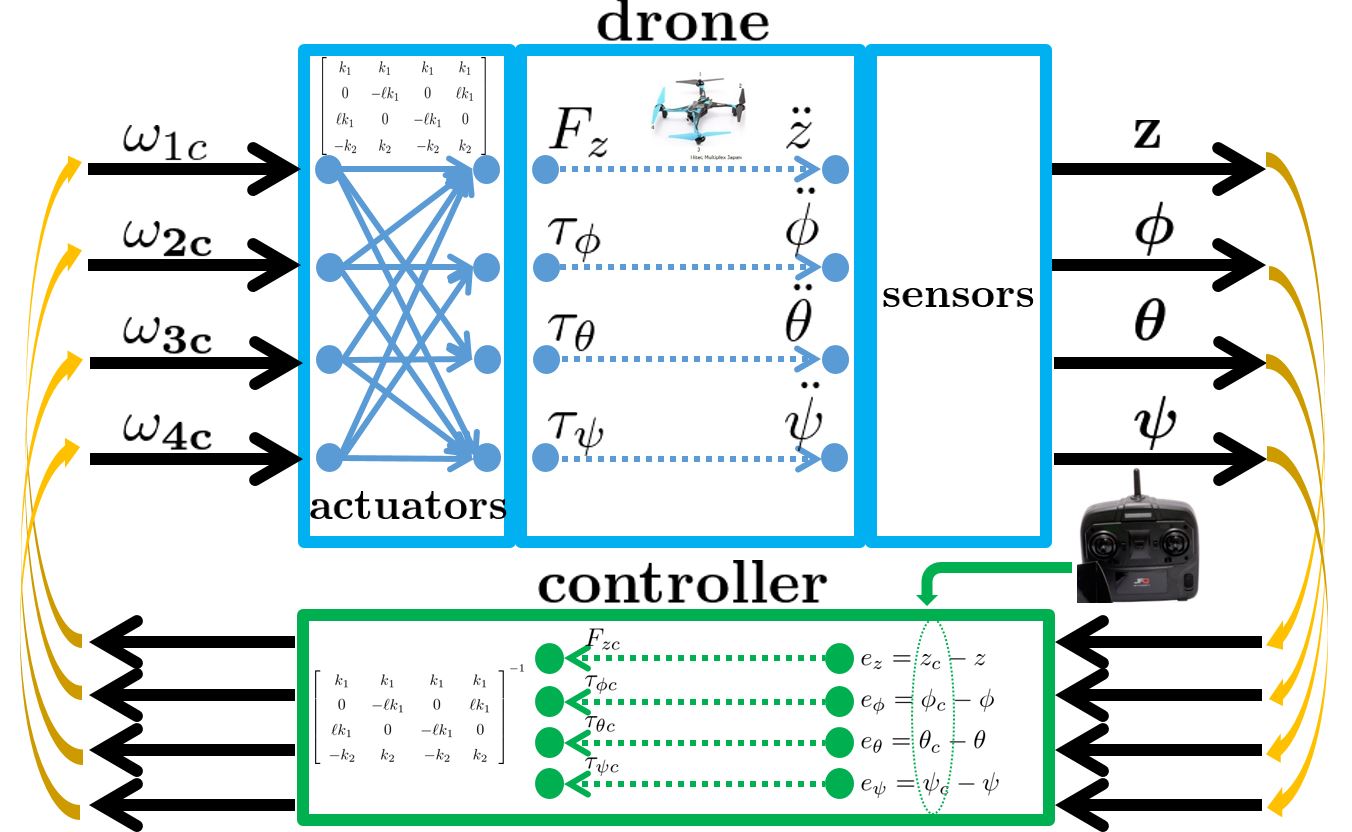
Then we can produce 1 force ![]() and 3 torques
and 3 torques ![]() ,
, ![]() ,
, ![]() to control the heave
to control the heave ![]() and the roll
and the roll ![]() , the pitch
, the pitch ![]() , the yaw
, the yaw ![]() respectively by combining the 4 propellers’ thrusts as follows:
respectively by combining the 4 propellers’ thrusts as follows:
![Rendered by QuickLaTeX.com \left[\begin{array}{c} F_z \\ \tau_\phi \\ \tau_\theta \\ \tau_\psi \end{array}\right]= \left[\begin{array}{cccc} k_1 & k_1 & k_1 & k_1 \\ 0 & -\ell k_1 & 0 & \ell k_1 \\ \ell k_1 & 0 & -\ell k_1 & 0 \\ -k_2 & k_2 & -k_2 & k_2 \end{array}\right] \left[\begin{array}{c} \omega_{1c} \\ \omega_{2c} \\ \omega_{3c} \\ \omega_{4c} \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d3669f562b1e9f2e469a009e277d047c_l3.png) .
.
This means that the MIMO dynamics is decoupled into 4 SISO dynamics. We will employ a PID controller corresponding to each SISO dynamics. Therefore it is the static decoupling to make the control system design easier.
●Many underwater vehicles have been developed for various purposes. For example, we can find them as follows.

Note that 4 to 8 thrustors are equipped to realize the static decoupling. The number depends on motion necessary to achieve the mission of UVs. Most control systems will be designed in the same way as drone.
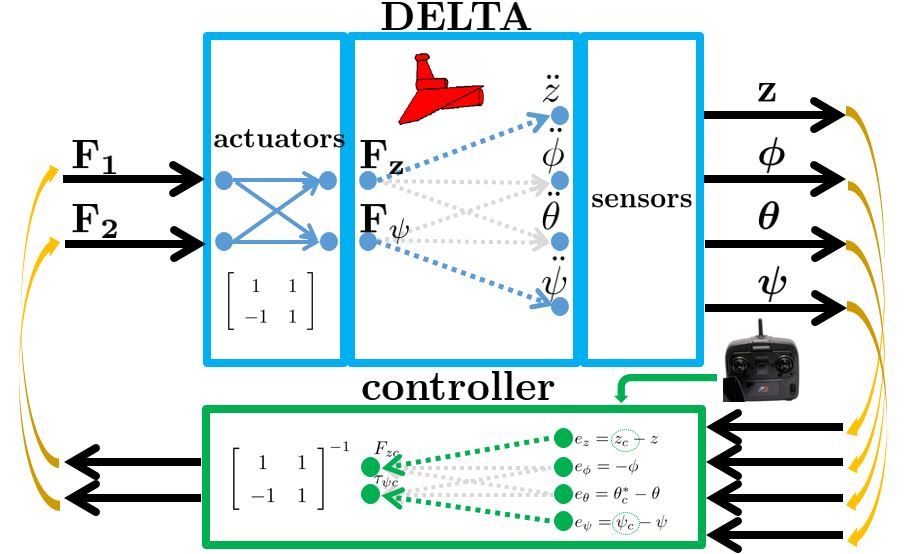
●Prof. Koterayama and Prof. Nakamura developed the following UV called as DELTA.

The mission of DELTA is for wide-area survey. It works in a towing mode for wade scanning, and in a self-propulsive mode for local investigation. The detail is discussed in the paper:
Masahiko NAKAMURA, Hiroyuki KAJIWARA, Wataru KOTERAYAMA:
Development of an ROV operated both as towed and self-propulsive vehicle
Ocean Engineering, vol.28, no.1, pp.1-43, 2000.
DELTA has only two thrustors. So only the heave ![]() and the yaw
and the yaw ![]() are controlled. However it is necessary to control the roll
are controlled. However it is necessary to control the roll ![]() and the pitch
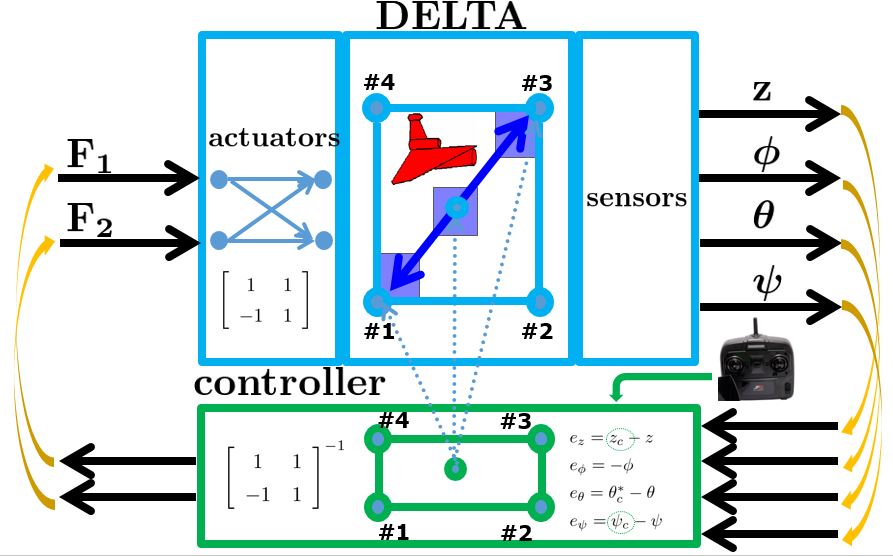
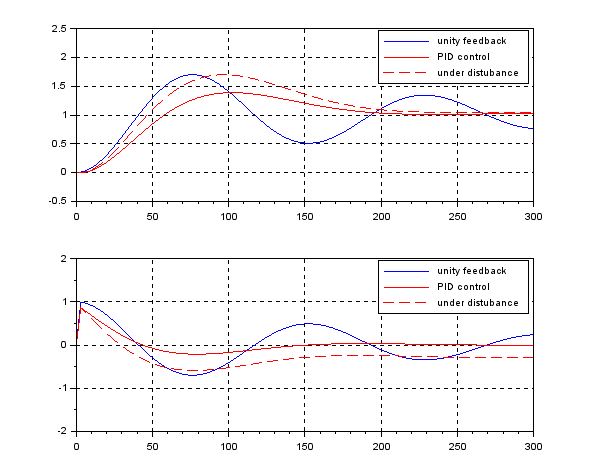
and the pitch ![]() to keep the equilibrium state. Such a control system can’t be realized by PID control. The following control system is designed by LQG approach.
to keep the equilibrium state. Such a control system can’t be realized by PID control. The following control system is designed by LQG approach.
For any UV, the collision avoidance is an important function. For example, a deep diving will be necessary to avoid an obstacle as follows.
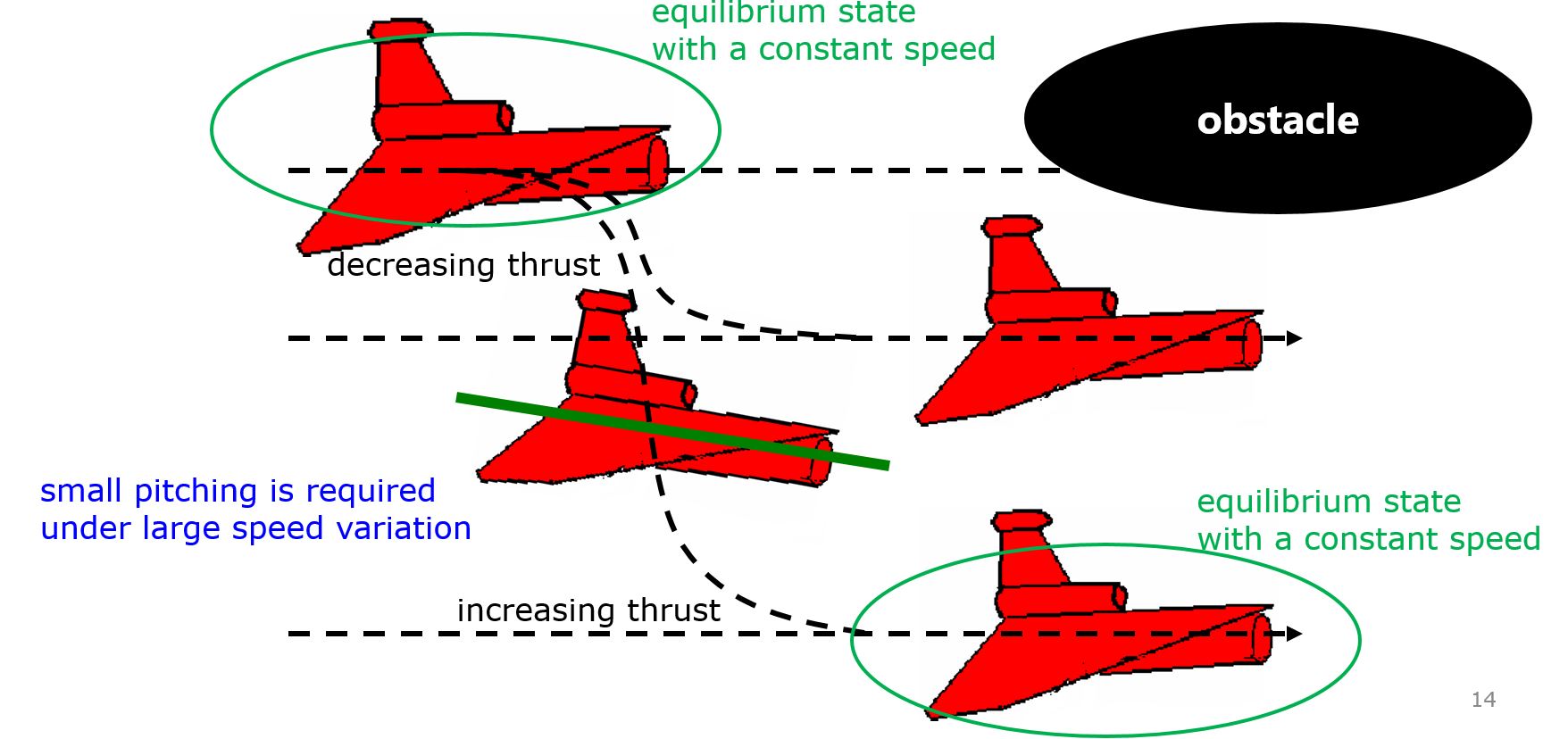
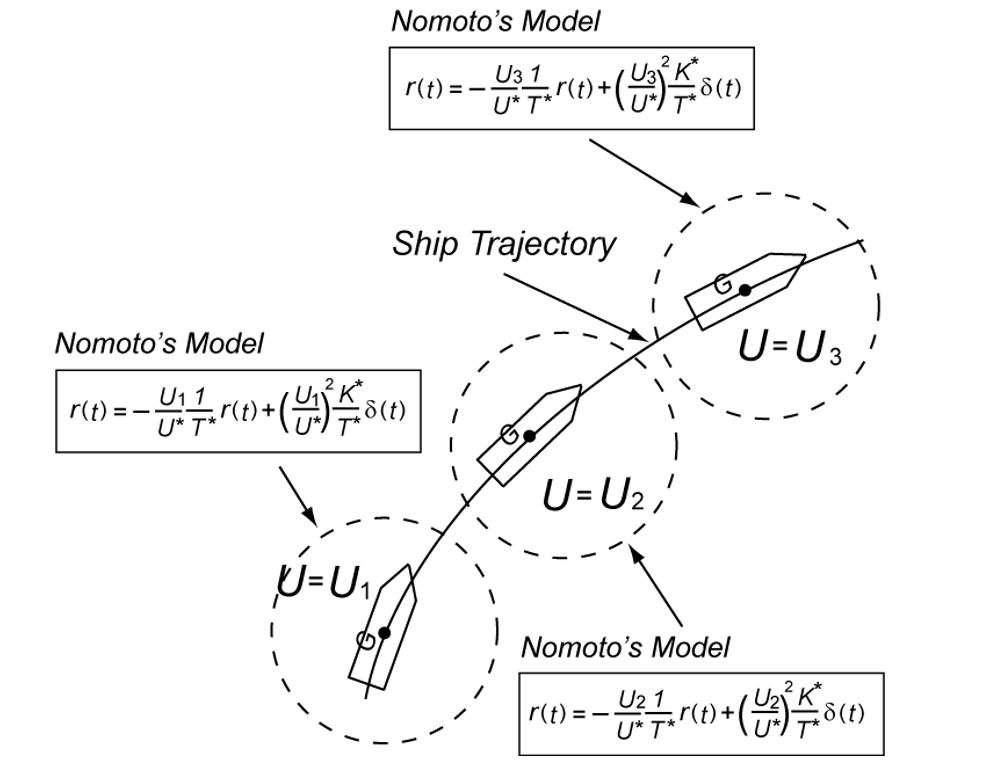
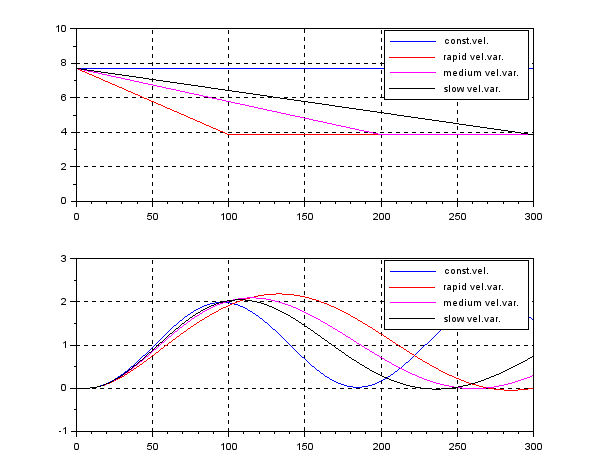
In order to change the depth in DELTA, there is no way except decreasing the thrust. This means the large speed variation, by which hydrodynamic force will be varied largely. So we need a robust controller or a scheduling controller. Such a control scheme is depicted in the following.
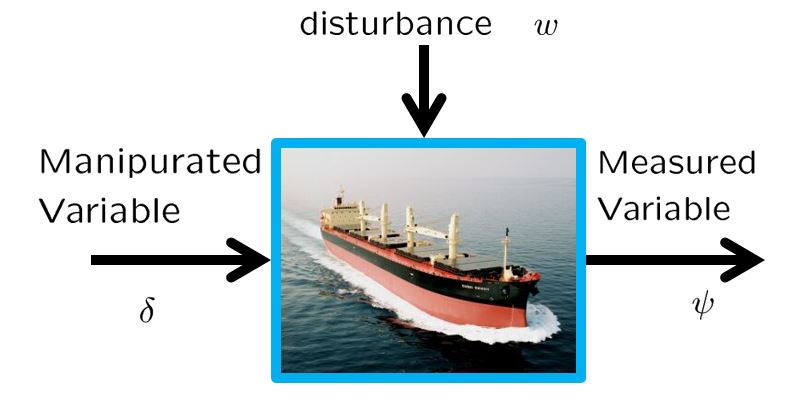
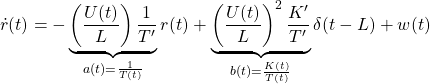
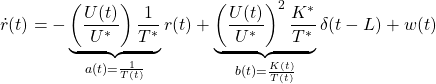
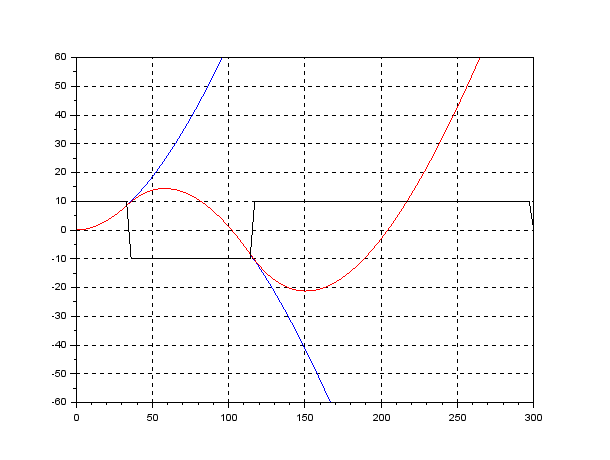
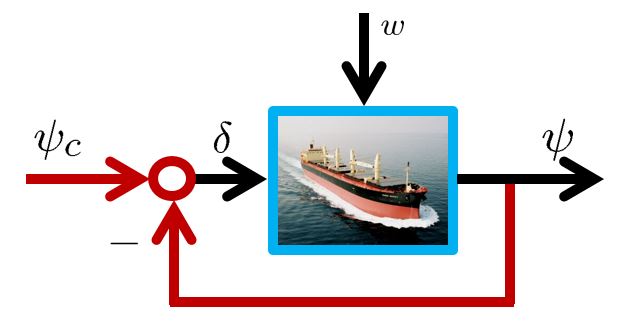
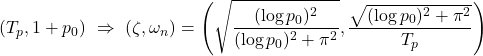
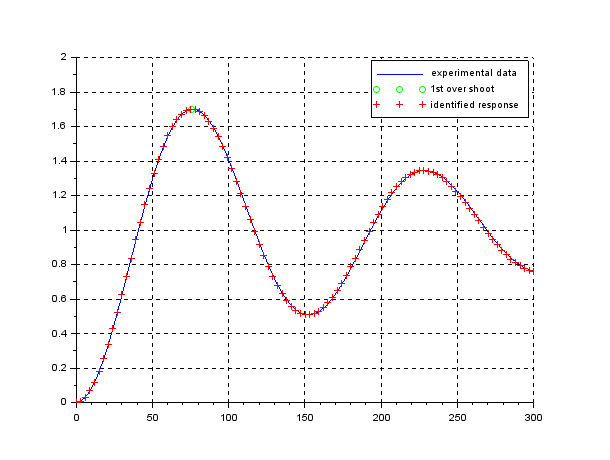
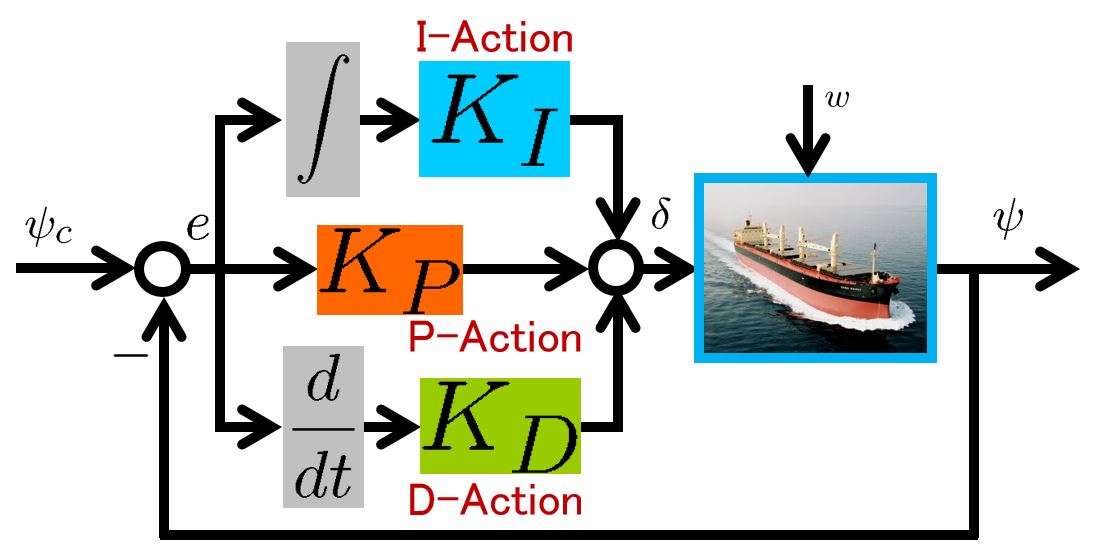
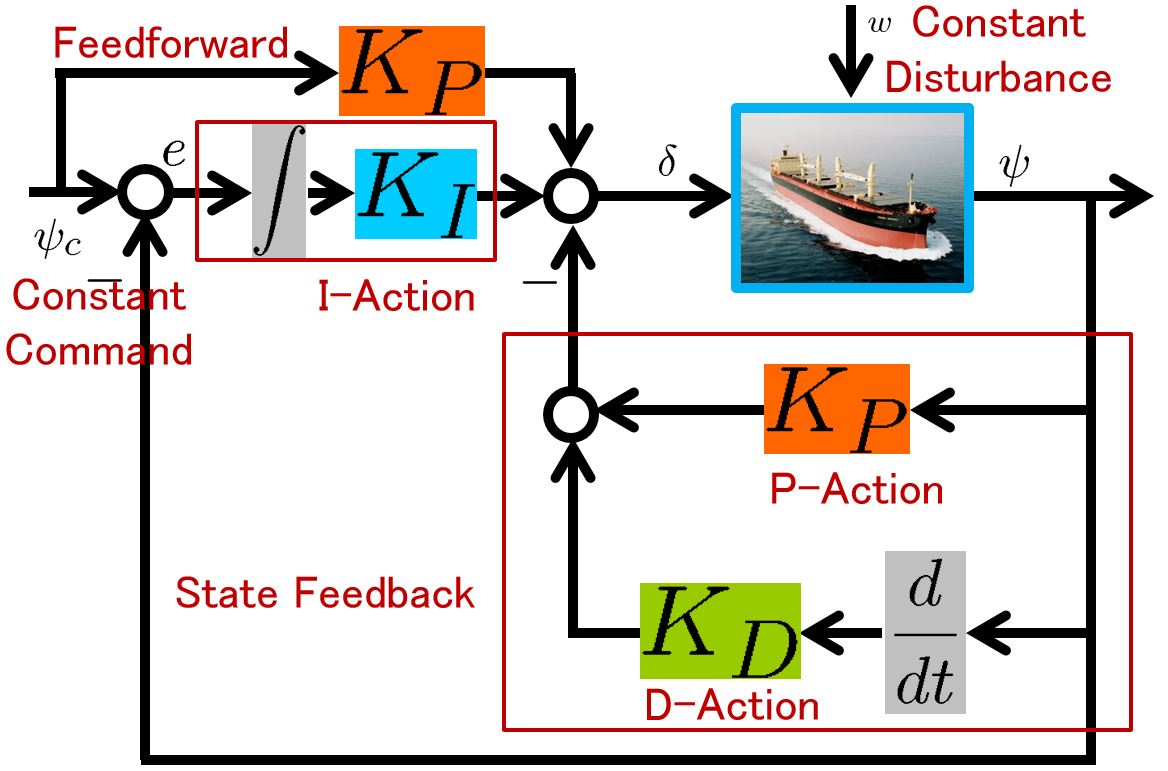
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{\psi}(t) \\ \dot{r}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \psi(t) \\ r(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] }_{B} \underbrace{\delta(t)}_{u(t)} + \left[\begin{array}{c} 0 \\ w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4a1aee5f6b09b2cdfe1ab7652b436682_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{\delta(t)}_{u(t)} =- \underbrace{ \left[\begin{array}{cc} K_P & K_D \end{array}\right] }_{F} \underbrace{ \left[\begin{array}{c} \psi(t) \\ r(t) \end{array}\right] }_{x(t)} +\underbrace{K_P}_{G} \underbrace{\psi_c}_{v} +K_I \underbrace{\int_0^t(\psi_c-\psi(\tau))\,d\tau}_{x_I(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-930108f8395d8a1e4622e3ba6c5474d0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{\psi}(t) \\ \dot{r}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_{CL}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ -\omega_n'^2 & -2\zeta'\omega_n' & \omega_I\omega_n'^2 \\ -1 & 0 & 0 \end{array}\right] }_{A_{CL}} \underbrace{ \left[\begin{array}{c} \psi(t) \\ r(t) \\ x_I(t) \end{array}\right] }_{x_{CL}(t)} + \underbrace{ \left[\begin{array}{cc} 0 & 0\\ \omega_n'^2 & 1\\ 1 & 0 \end{array}\right] }_{B_{CL}} \left[\begin{array}{c} \psi_c \\ w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6220f1085c08a4300d1c579caa0ed438_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \ddot{\psi}(t) \\ \ddot{r}(t) \\ \ddot{x}_I(t) \end{array}\right] }_{\ddot{x}_{CL}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ -\omega_n'^2 & -2\zeta'\omega_n' & \omega_I\omega_n'^2 \\ -1 & 0 & 0 \end{array}\right] }_{A_{CL}} \underbrace{ \left[\begin{array}{c} \dot{\psi}(t) \\ \dot{r}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_{CL}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-968db1b1514ee0d76247eda68498a63d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \psi(t) \\ r(t) \\ x_I(t) \end{array}\right] }_{x_{CL}} \rightarrow \underbrace{ \left[\begin{array}{ccc} 0 & -1 & 0\\ \omega_n'^2 & 2\zeta'\omega_n' & -\omega_I\omega_n'^2 \\ 1 & 0 & 0 \end{array}\right]^{-1} }_{-A_{CL}^{-1}} \underbrace{ \left[\begin{array}{cc} 0 \\ \omega_n'^2\psi_c +w\\ \psi_c \end{array}\right] }_{B_{CL}} = \left[\begin{array}{cc} \psi_c\\ 0\\ \frac{w}{\omega_I\omega_n'^2} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cb5b3a5683705b70ec4dd15795c1b402_l3.png)
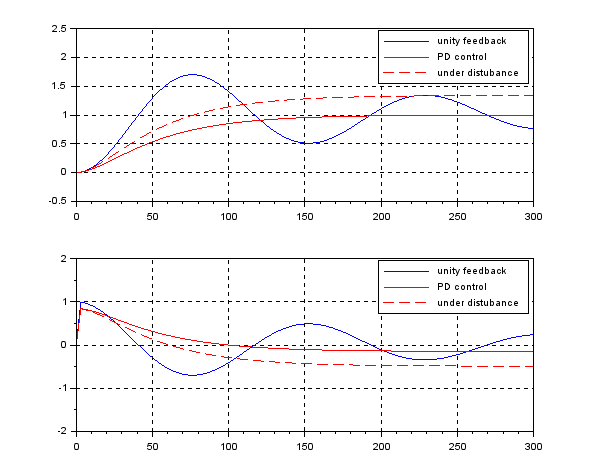
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot\psi(t)-\dot{\psi}_c \\ \dot r(t) \\ \dot{\delta}(t) \end{array}\right] = \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & -2\zeta\omega_n &\omega_n^2 \\ 0 & 0 & 0 \end{array}\right] \left[\begin{array}{c} \psi(t)-\psi_c \\ r(t) \\ \delta(t) \end{array}\right] + \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right] \dot{\delta} (t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-070f96da6e302ea77182e63b89b5daad_l3.png)
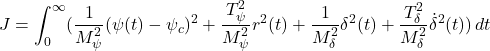
![Rendered by QuickLaTeX.com \displaystyle{ \dot{\delta}(t) =- \left[\begin{array}{ccc} f_\psi & f_r & f_\delta \end{array}\right] \left[\begin{array}{c} \psi(t)-\psi_c \\ r(t) \\ \delta(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-78bdbd6a02cdc112e35492f7b66c2813_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ =- \underbrace{ \left[\begin{array}{ccc} f_\psi & f_r & f_\delta \end{array}\right] \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & -2\zeta\omega_n &\omega_n^2 \\ 1 & 0 & 0 \end{array}\right]^{-1} }_{ \left[\begin{array}{ccc} K_P & K_D & K_I \end{array}\right] } \left[\begin{array}{c} \dot\psi(t)-\dot{\psi}_c \\ \dot{r}(t) \\ \psi(t)-\psi_c \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bfcd4ed97bb6d3d92a95153aacf8d555_l3.png)
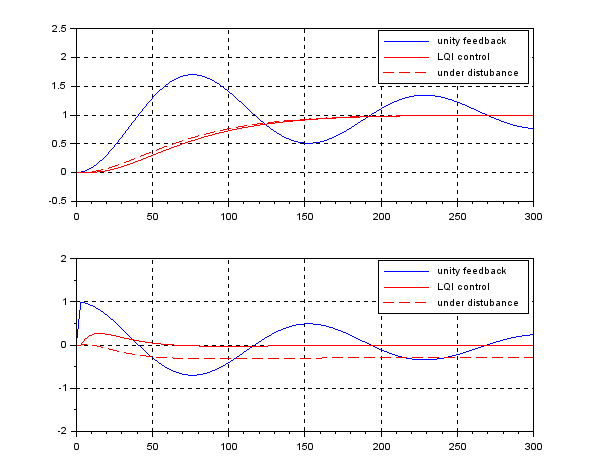
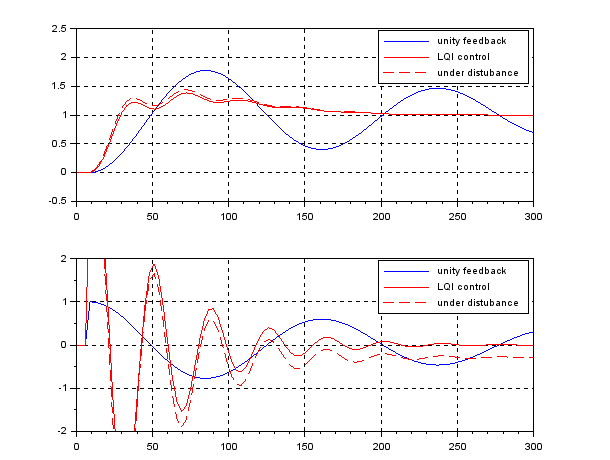
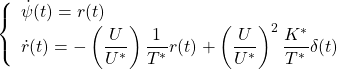
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{\psi}(t) \\ \dot{r}(t) \\ \dot{\delta}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ 0 & -\left(\frac{U}{U^*}\right)\frac{1}{T^*} & \left(\frac{U}{U^*}\right)^2\frac{K^*}{T^*} \\ 0 & 0 & -\frac{1}{T_a} \end{array}\right] }_{A(U,U^2)} \underbrace{ \left[\begin{array}{c} \psi(t) \\ r(t) \\ \delta(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ \frac{K_a}{T_a} \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3d725574d98be967189e786862a42f9a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \psi(t) }_{y(t)} = \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \psi(t) \\ r(t) \\ \delta(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-067f0588c517bfa5ab508b0cb5faafb1_l3.png)
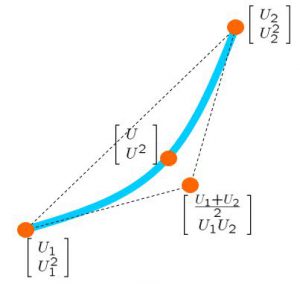
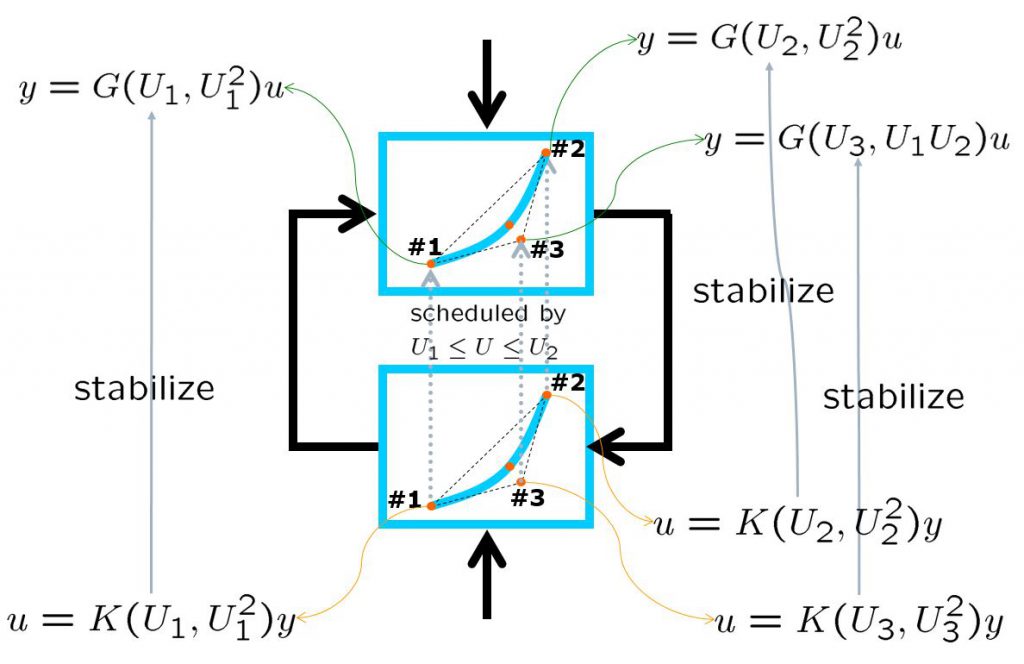
![Rendered by QuickLaTeX.com \displaystyle{ P: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x} \\ \dot{x}_I \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A(U,U^2)& 0 \\ -C & 0 \end{array}\right] }_{\cal{A}(U,U^2)} \left[\begin{array}{c} x \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_1} r + \underbrace{\left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_2} u\\ \underbrace{ \left[\begin{array}{c} y_{11} \\ y_{12} \end{array}\right] }_{y_1} = \underbrace{ \left[\begin{array}{cc} 0 &\omega_I\\ \omega_DCA(U,U^2) & 0 \end{array}\right] }_{C_1} \left[\begin{array}{c} x \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \end{array}\right] }_{D_{11}} r + \underbrace{ \left[\begin{array}{c} 0 \\ \omega_DCB \end{array}\right] }_{D_{12}} u\\ \underbrace{ \left[\begin{array}{c} y \\ x_I \end{array}\right] }_{y_2} = \underbrace{ \left[\begin{array}{cc} C & 0\\ 0 & 1 \end{array}\right] }_{C_2} \left[\begin{array}{c} x \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \end{array}\right] }_{D_{21}} r \end{array}\right.}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-53e2d7d1439b485ab0a651fb593485bc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ K_0: \left\{\begin{array}{l} \dot{x}_K=A_K(U,U^2)x_K+ \underbrace{ \left[\begin{array}{cc} B_K^{(1)}(U,U^2) & B_K^{(2)}(U,U^2) \end{array}\right] }_{B_K(U,U^2)} \left[\begin{array}{c} y \\ x_I \end{array}\right] \\ u=C_K(U,U^2)x_K + \underbrace{ \left[\begin{array}{cc} D_K^{(1)}(U,U^2) & D_K^{(2)}(U,U^2) \end{array}\right] }_{D_K(U,U^2)} \left[\begin{array}{c} y \\ x_I \end{array}\right] \end{array}\right.}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-54e444239e49a80798f6b2b19731a663_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ K: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_K \\ \dot{x}_I \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A_K(U,U^2) & B_K^{(2)}(U,U^2) \\ 0 & 0 \end{array}\right] }_{A_K(U,U^2)} \left[\begin{array}{c} x_K \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{cc} B_K^{(1)}(U,U^2) & 0\\ -1& 1 \end{array}\right] }_{B_K(U,U^2)} \left[\begin{array}{c} y \\ r \end{array}\right] \\ u= \underbrace{ \left[\begin{array}{cc} C_K(U,U^2) & D_K^{(2)}(U,U^2) \end{array}\right] }_{C_K(U,U^2)} \left[\begin{array}{c} x_K \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{cc} D_K^{(1)}(U,U^2) & 0 \end{array}\right] }_{D_K(U,U^2)} \left[\begin{array}{c} y \\ r \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c54a60ae350f5490f5fc7c4c58f49a2b_l3.png)
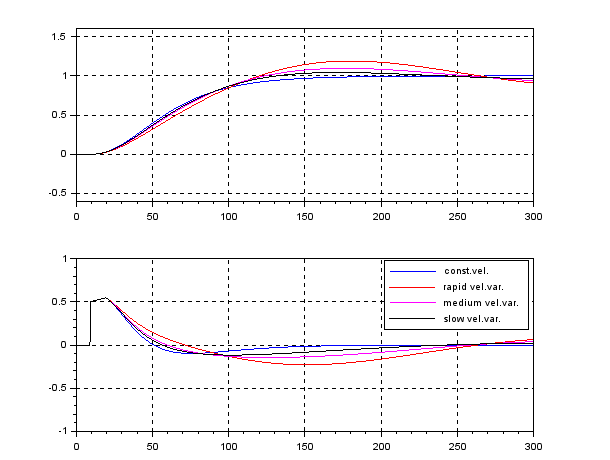
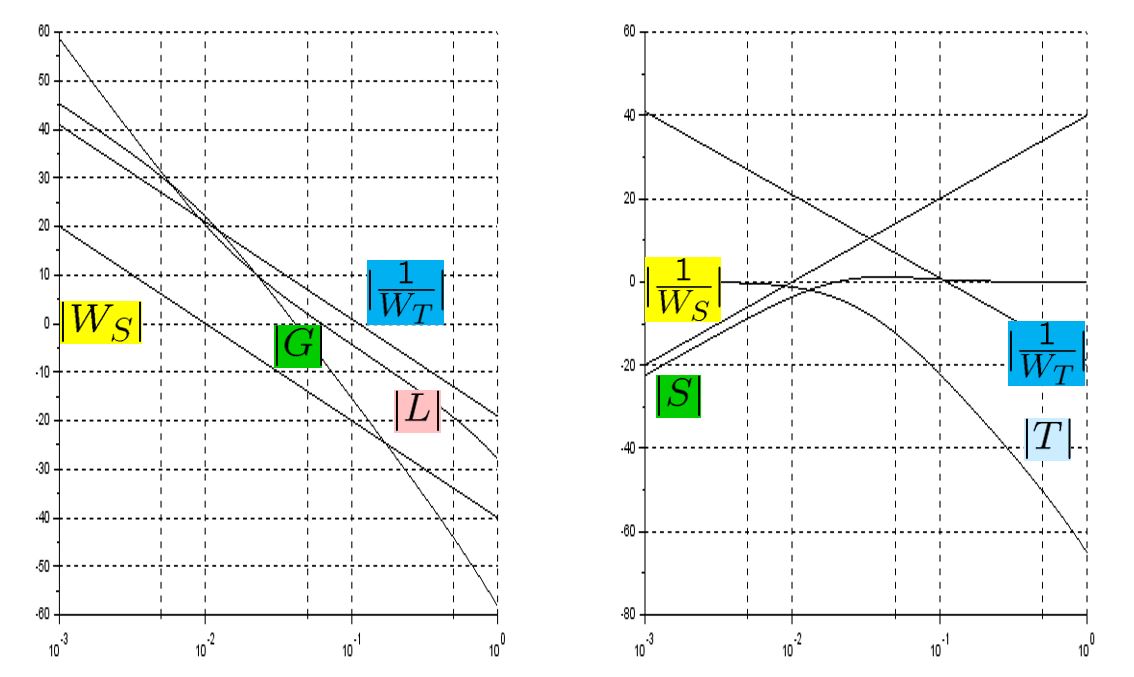
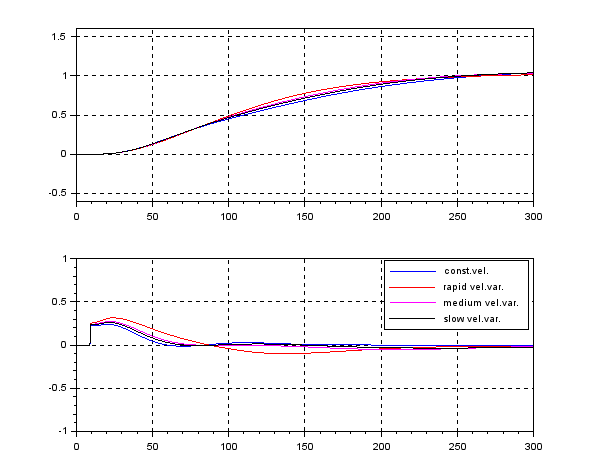
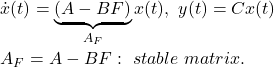
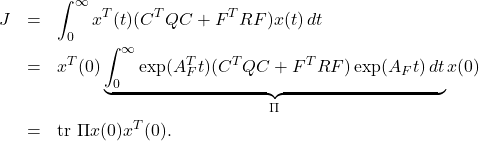
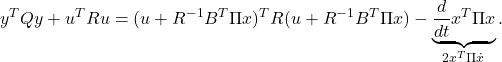
![Rendered by QuickLaTeX.com \begin{eqnarray*} && \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] + \left[\begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \nonumber\\ &&-\left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ 1 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] + \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \nonumber , \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8451bf77f93103b4b977badfda8b557b_l3.png)
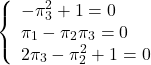
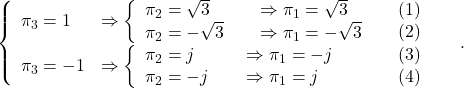
![Rendered by QuickLaTeX.com \begin{eqnarray*} \underbrace{ \left[\begin{array}{cc} A & -BR^{-1}B^T \\ -C^TQC & -A^T \end{array}\right]}_{M(2n\times 2n)} \underbrace{ \left[\begin{array}{c} V_1 \\ V_2 \end{array}\right]}_{V^-(2n\times n)} = \underbrace{ \left[\begin{array}{c} V_1 \\ V_2 \end{array}\right]}_{V^-(2n\times n)} \underbrace{ {\rm diag}\{\lambda_1,\cdots,\lambda_n\} }_{\Lambda^-(n\times n)}. \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6134fe44b7b15f5c2ed017d856889b8b_l3.png)
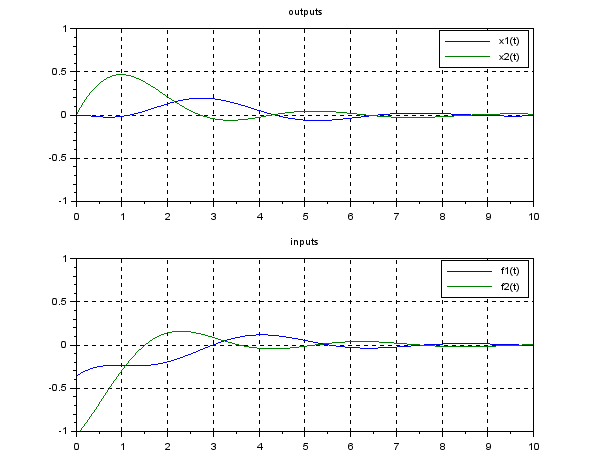
![Rendered by QuickLaTeX.com \begin{eqnarray*} \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \ddot{x}_1(t) \\ \ddot{x}_2(t) \\ \end{array}\right] }_{\dot{x}(t)} &=& \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -\frac{k}{m_1} & -\frac{k}{m_1} & 0 & 0 \\ \frac{k}{m_2} & -\frac{k}{m_2}& 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{x(t)}\\ &&+ \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \frac{k}{m_1} & 0 \\ 0 & \frac{k}{m_2} \end{array}\right] }_{B} \underbrace{ \left[\begin{array}{c} f_1(t) \\ f_2(t) \end{array}\right] }_{u(t)}, \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2d4ea85cc25cd0f7c8c3404af6ff3979_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] }_{y(t)} &=&- \underbrace{ \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{x(t)}. \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-611550582beb0b3ed91eb51c1a672f96_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[\begin{array}{c} {x}_1(0) \\ {x}_2(0) \\ \dot{x}_1(0) \\ \dot{x}_2(0) \\ \end{array}\right] = \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ \frac{k}{m_2} \end{array}\right] \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3699ab4b4d4527cb552796332d8087f_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} \underbrace{ \left[\begin{array}{c} f_1(t) \\ f_2(t) \end{array}\right] }_{u(t)} &=&- \underbrace{ \left[\begin{array}{cccc} g_{11} & g_{12} & g_{13} & g_{14} \\ g_{21} & g_{22} & g_{23} & g_{24} \end{array}\right] }_{F} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{x(t)}. \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-534b70a7ee454caba7d663c5dba90e8f_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} J&=&\int_0^\infty ( \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right]^T }_{y^T(t)} \underbrace{ \left[\begin{array}{cc} q_1^2 & 0 \\ 0 & q_2^2 \ \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] }_{y(t)}\\ &&+\underbrace{ \left[\begin{array}{c} f_1(t) \\ f_2(t) \end{array}\right]^T }_{u^T(t)} \underbrace{ \left[\begin{array}{cc} r_1^2 & 0 \\ 0 & r_2^2 \ \end{array}\right] }_{R} \underbrace{ \left[\begin{array}{c} f_1(t) \\ f_2(t) \end{array}\right] }_{u(t)} )\,dt. \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e39ecdd42eaf2ef9fcad46841e42ca20_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&[\frac{\partial}{\partial X}{\rm tr}AXB]_{ij} =\frac{\partial}{\partial x_{ij}}\sum_{k}[AXB]_{kk} =\frac{\partial}{\partial x_{ij}}\sum_{k}\sum_{i,j}a_{ki}x_{ij}b_{jk}\\ &&=\sum_{k}b_{jk}a_{ki}=[BA]_{ji}=[A^TB^T]_{ij}, \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-05455a1f26f5ab87bf6b1f0503ea4df8_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&[\frac{\partial}{\partial X}{\rm tr}AX^TB]_{ij} =\frac{\partial}{\partial x_{ij}}\sum_{k}[AX^TB]_{kk} =\frac{\partial}{\partial x_{ij}}\sum_{k}\sum_{i,j}a_{ki}x_{ji}b_{jk}\\ &&=\sum_{k}b_{ik}a_{kj}=[BA]_{ij}, \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-98102e722ac70c87430ce9f0a0f5f96a_l3.png)
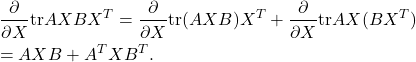
![Rendered by QuickLaTeX.com \begin{eqnarray*} J_x&=&\int_0^\infty q^2x^2(t)\,dt \nonumber\\ &=&\int_0^\infty q^2e^{2(a-bf)t}x^2(0)\,dt \nonumber\\ &=&q^2x^2(0)\left[\frac{1}{2(a-bf)}e^{2(a-bf)t}\right]_0^\infty \nonumber\\ &=&\frac{q^2x^2(0)}{2(a-bf)}\left[\underbrace{e^{2(a-bf)\infty}}_{0}-\underbrace{e^{2(a-bf)0}}_{1}\right] \nonumber\\ &=&-\frac{q^2}{2(a-bf)}x^2(0)>0\quad (a-bf<0), \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7559be4064d055fb7cda05e82615d8a7_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} J_u&=&\int_0^\infty r^2u^2(t)\,dt \nonumber\\ &=&\int_0^\infty r^2f^2e^{2(a-bf)t}x^2(0)\,dt \nonumber\\ &=&r^2f^2x^2(0)\left[\frac{1}{2(a-bf)}e^{2(a-bf)t}\right]_0^\infty \nonumber\\ &=&-\frac{r^2f^2}{2(a-bf)}x^2(0)>0\quad (a-bf<0). \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cc45ca8495790c6bd637a24e40a72189_l3.png)
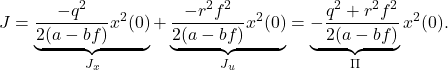
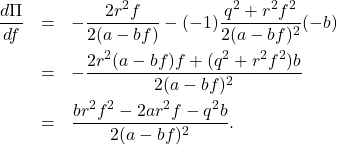
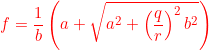
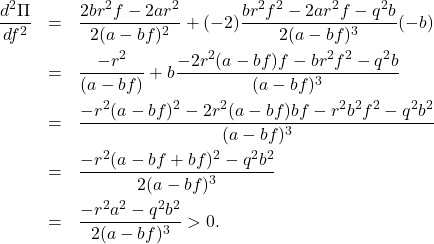
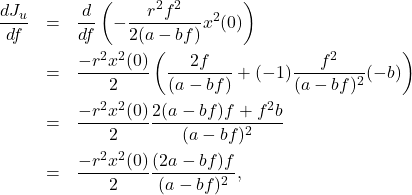
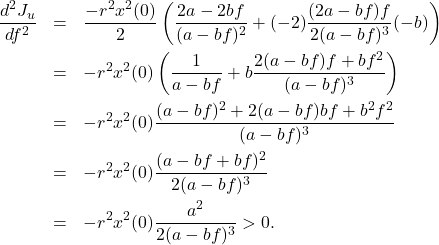
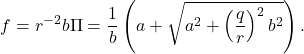
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[\begin{array}{cc} v_1 \\ v_2 \end{array}\right] =\left[\begin{array}{cc} 1 \\ \frac{-a-\sqrt{a^2+r^{-2}b^2q^2}}{-r^{-2}b^2} \end{array}\right] \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-054e996fc3498f6cf60565cada2b6d52_l3.png)
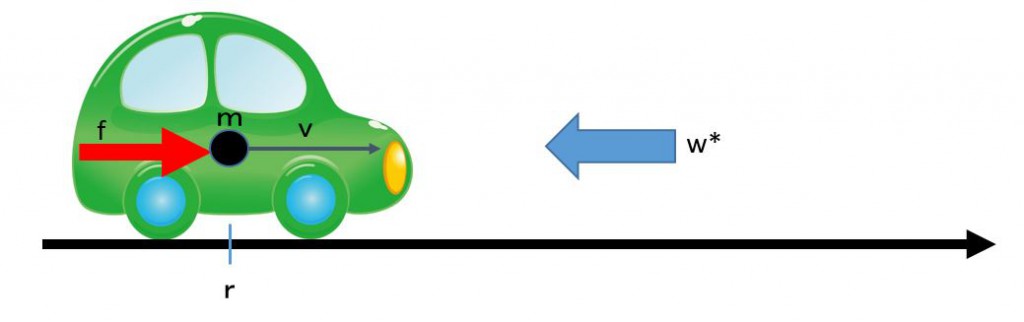
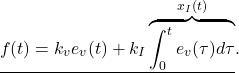
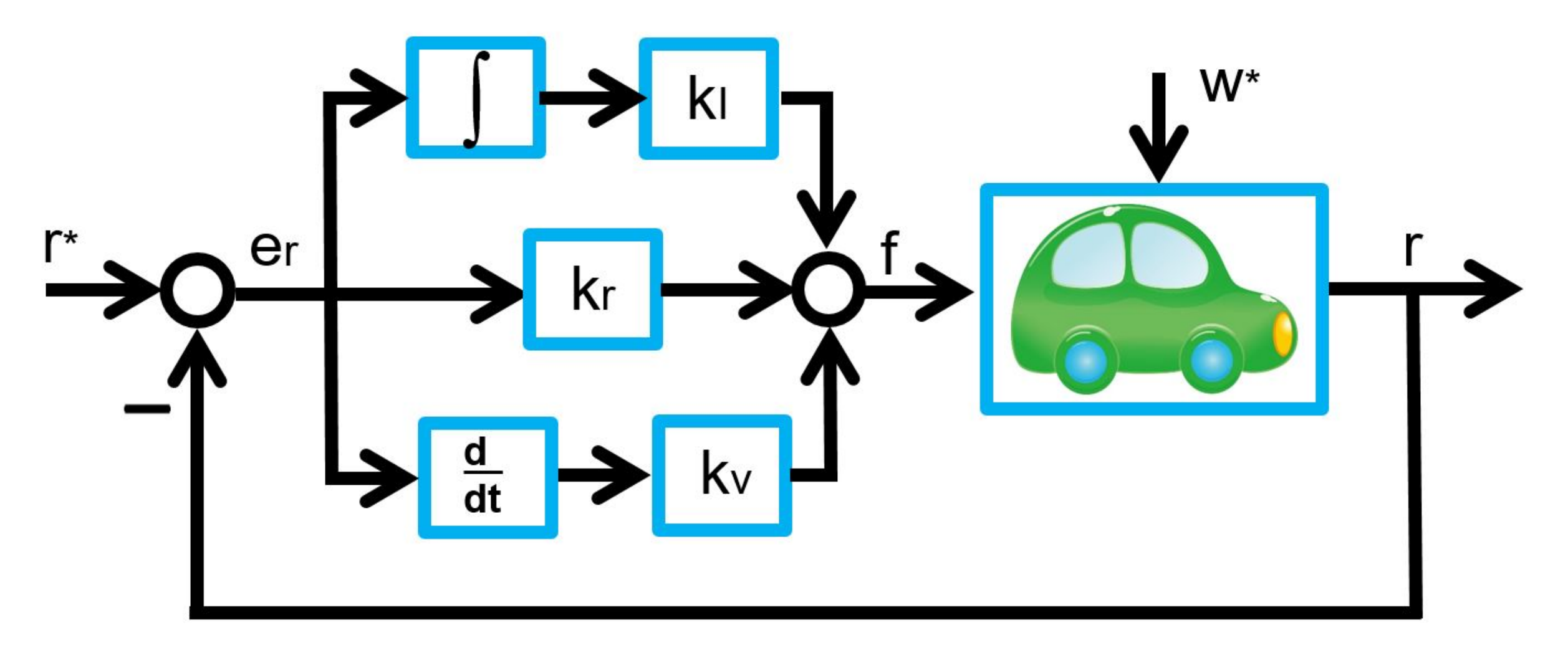
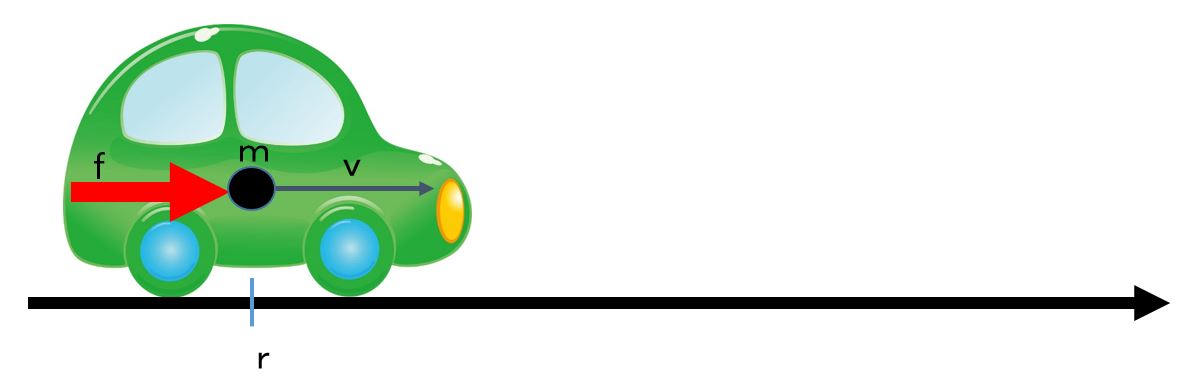
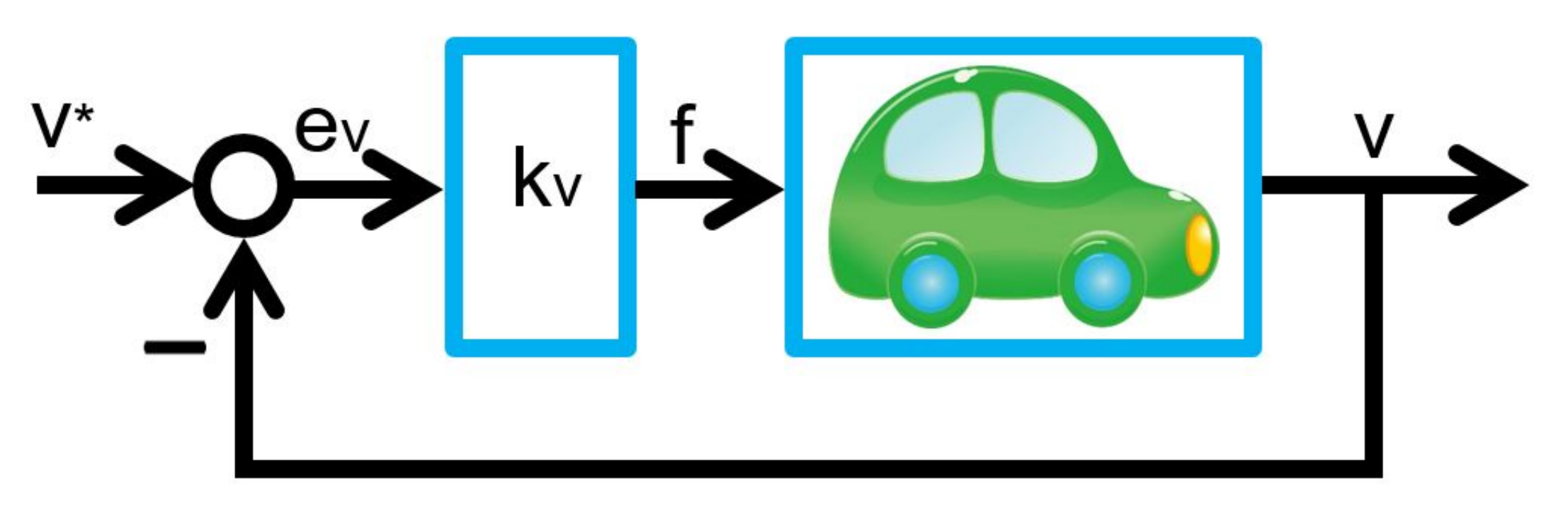
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[\begin{array}{c} \dot{e}_v(t) \\ \dot{x}_I(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} -\frac{k_v}{m} & -\frac{k_I}{m}\\ 1 & 0 \\ \end{array}\right] }_{A} \left[\begin{array}{c} e_v(t) \\ x_I(t) \end{array}\right] + \left[\begin{array}{c} -\frac{1}{m}w^* \\ 0 \end{array}\right]. \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c81ccfb6e56446c8b820d16517f3e92b_l3.png)
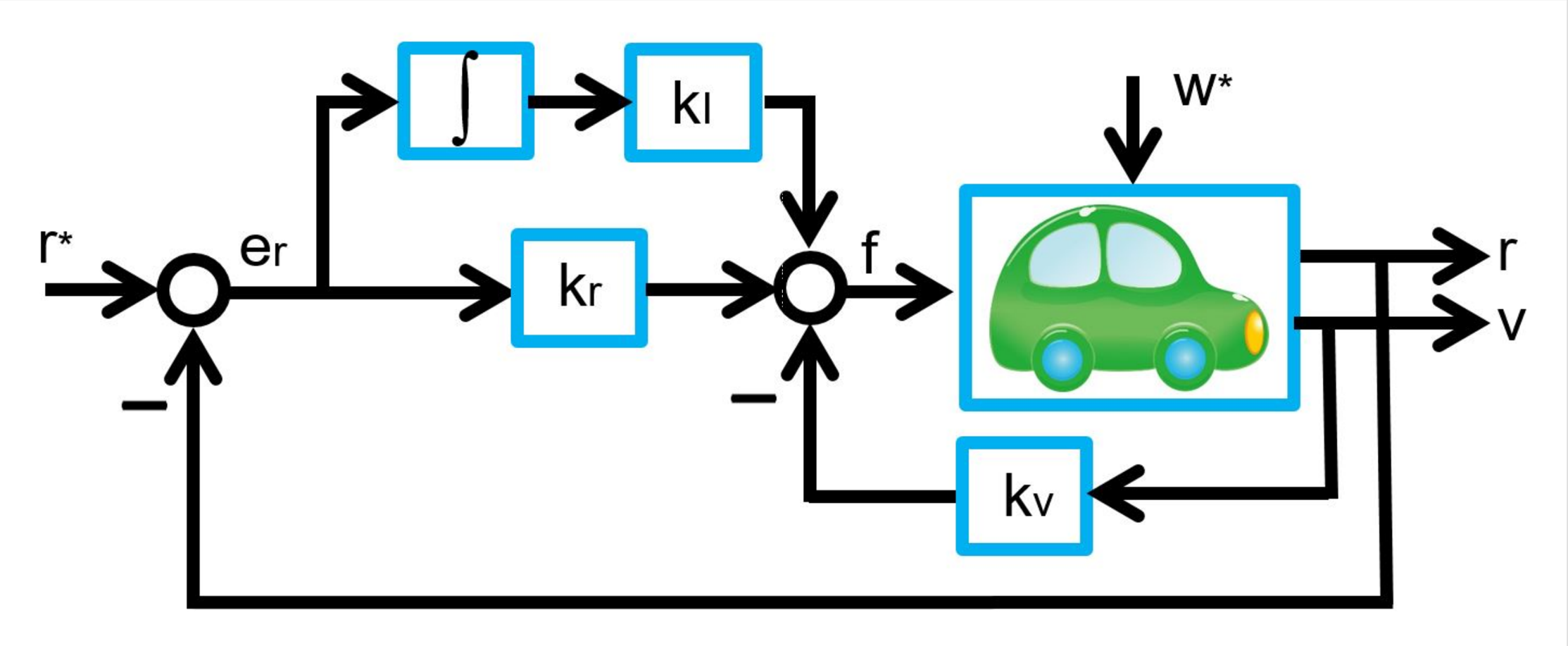
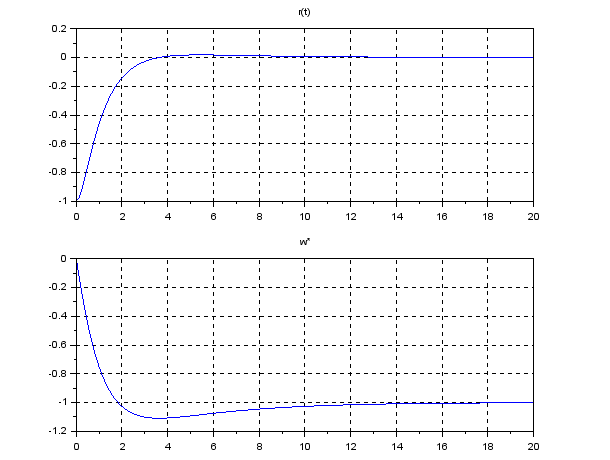
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\left[\begin{array}{c} e_v(t) \\ x_I(t) \end{array}\right] \rightarrow -\left[\begin{array}{cc} -\frac{k_v}{m} & -\frac{k_I}{m}\\ 1 & 0 \\ \end{array}\right]^{-1} \left[\begin{array}{c} -\frac{1}{m}w^* \\ 0 \end{array}\right]\\ &&=\frac{m}{k_I} \left[\begin{array}{cc} 0 & \frac{k_I}{m}\\ -1 & -\frac{k_v}{m} \\ \end{array}\right] \left[\begin{array}{c} \frac{1}{m}w^* \\ 0 \end{array}\right] =\left[\begin{array}{c} 0\\ -\frac{1}{k_I}w^* \end{array}\right]. \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8b709be2f21a0ec785f3c2f35592c509_l3.png)

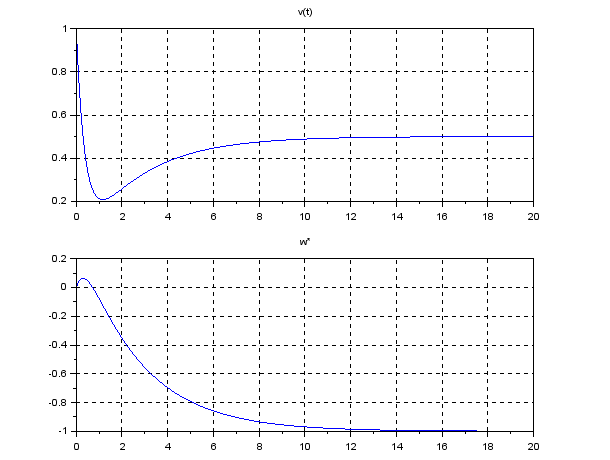
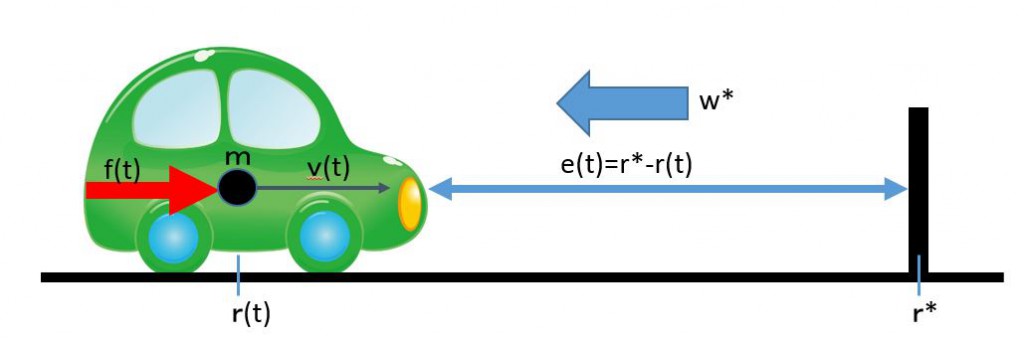
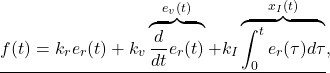
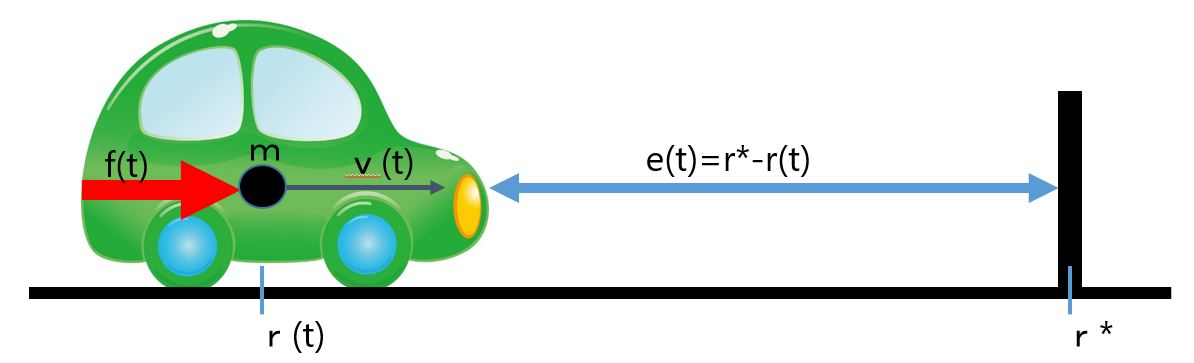
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[\begin{array}{c} \dot{e}_r(t) \\ \dot{e}_v(t) \\ \dot{x}_I(t) \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ -\frac{k_r}{m} & -\frac{k_v}{m} & -\frac{k_I}{m}\\ 1 & 0 & 0\\ \end{array}\right] }_{A} \left[\begin{array}{c} e_r(t) \\ e_v(t) \\ x_I(t) \end{array}\right] + \left[\begin{array}{c} 0\\ -\frac{1}{m}w^* \\ 0 \end{array}\right]. \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-53141a0f14185611b47b74f894f9dfa1_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\left[\begin{array}{c} e_r(t) \\ e_v(t) \\ x_I(t) \end{array}\right] \rightarrow -\left[\begin{array}{ccc} 0 & 1 & 0\\ -\frac{k_r}{m} & -\frac{k_v}{m} & -\frac{k_I}{m}\\ 1 & 0 & 0\\ \end{array}\right]^{-1} \left[\begin{array}{c} 0 \\ -\frac{1}{m}w^* \\ 0 \end{array}\right]\\ &&= \left[\begin{array}{ccc} 0 & 0 & 1\\ 1 & 0 & 0\\ -\frac{k_v}{k_I} & -\frac{m}{k_I} & -\frac{k_r}{k_I} \end{array}\right] \left[\begin{array}{c} 0 \\ \frac{1}{m}w^* \\ 0 \end{array}\right] =\left[\begin{array}{c} 0\\ 0\\ -\frac{1}{k_I}w^* \end{array}\right]. \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ad9784df54b62349489e8a97bc7e01dd_l3.png)
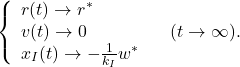
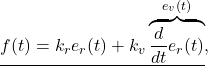
![Rendered by QuickLaTeX.com \begin{eqnarray*} \underbrace{ \left[\begin{array}{c} \dot{e}_r(t) \\ \dot{e}_v(t) \end{array}\right] }_{\dot{e}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{k_r}{m} & -\frac{k_v}{m} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} e_r(t) \\ e_v(t) \end{array}\right] }_{e(t)}. \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f97b79bd949dcc0d2e6ffafe1fae26e2_l3.png)
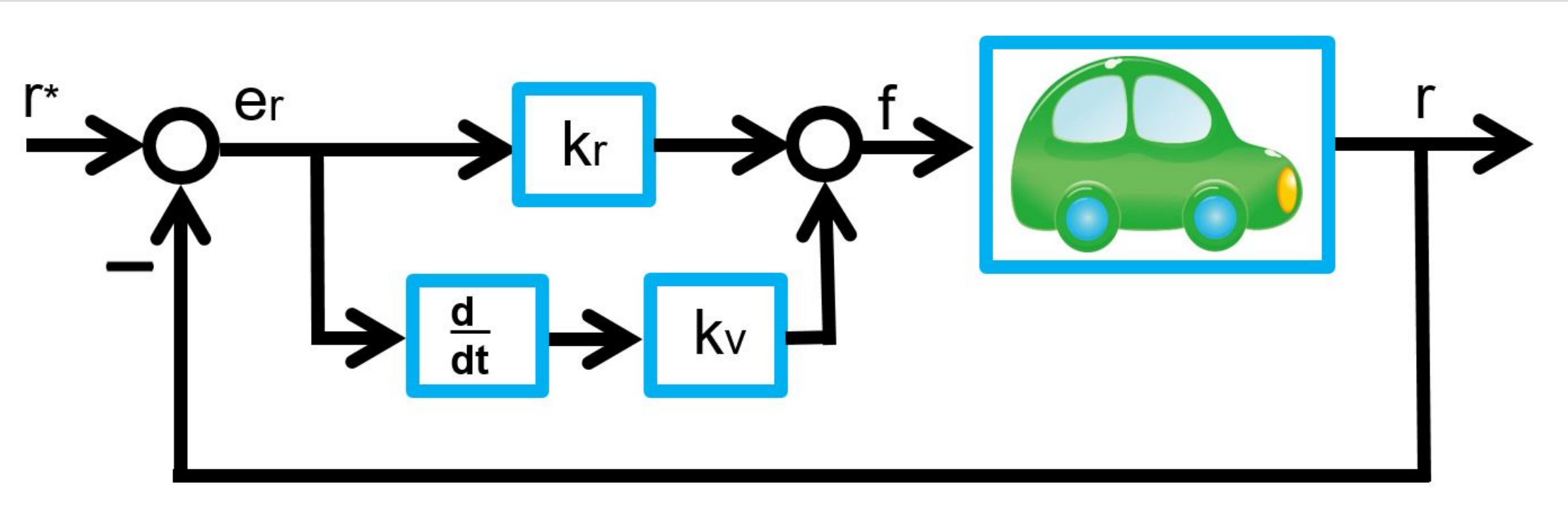
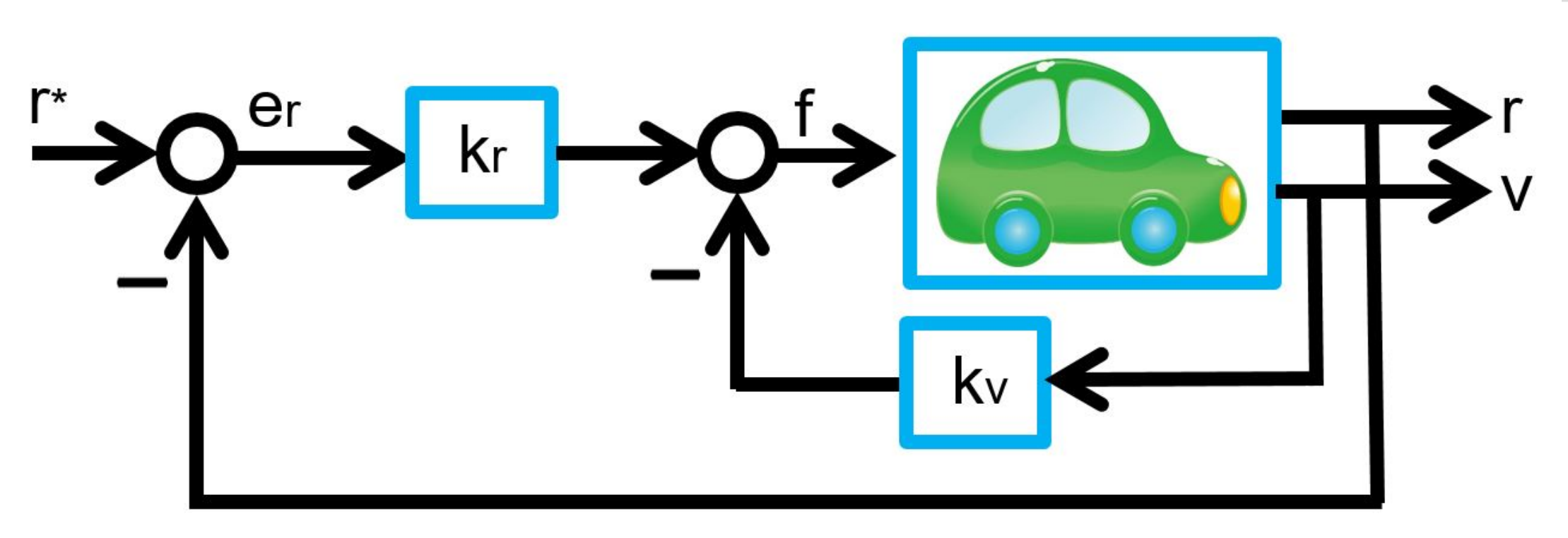
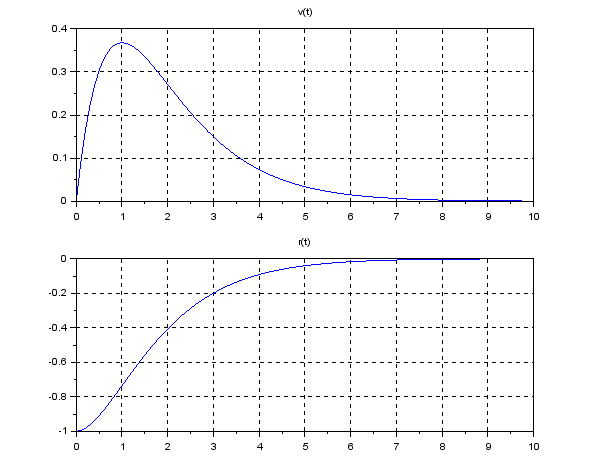
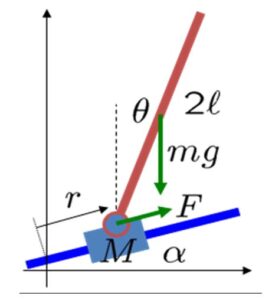
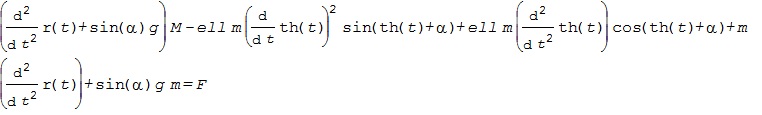
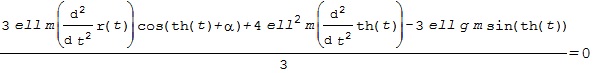
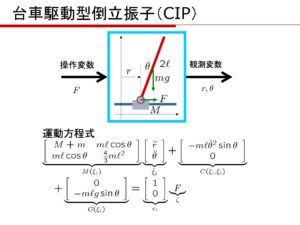
![Rendered by QuickLaTeX.com \xi= \left[\begin{array}{c} \xi_1 \\ \xi_2 \end{array}\right] = \left[\begin{array}{c} r \\ \theta \\ \dot{r} \\ \dot{\theta} \end{array}\right],\ \zeta=F](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b0388783ea269a17a07e587b3858ec56_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ f(\xi,\zeta)= \left[\begin{array}{c} f_1(\xi,\zeta) \\ f_2(\xi,\zeta) \\ f_3(\xi,\zeta) \\ f_4(\xi,\zeta) \end{array}\right]= \left[\begin{array}{c} f_1(r,\theta,\dot{r},\dot{\theta},F) \\ f_2(r,\theta,\dot{r},\dot{\theta},F) \\ f_3(r,\theta,\dot{r},\dot{\theta},F) \\ f_4(r,\theta,\dot{r},\dot{\theta},F) \end{array}\right]= \left[\begin{array}{c} {\xi}_2 \\ M^{-1}(\xi_1)(e_1\zeta-C(\xi_1){\xi}_2-G(\xi_1)) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-00729f634057c8db1004528a22f4155a_l3.png)
![Rendered by QuickLaTeX.com \xi^*= \left[\begin{array}{c} \xi^*_1 \\ \xi^*_2 \end{array}\right]= \left[\begin{array}{c} r^* \\ \theta^* \\ \dot{r}^* \\ \dot{\theta}^* \end{array}\right]= \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \end{array}\right]\ or\ \left[\begin{array}{c} 0 \\ \pi \\ 0 \\ 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8f1c442239e419bdc4574e49225aa032_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \frac{\partial f(\xi^*,\zeta^*)}{\partial\xi} =\left.\left[\begin{array}{cccc} \frac{\partial f_1}{\partial r} & \frac{\partial f_1}{\partial\theta} &\frac{\partial f_1}{\partial\dot{r}} & \frac{\partial f_1}{\partial\dot{\theta}} \\ \frac{\partial f_2}{\partial r} & \frac{\partial f_2}{\partial\theta} &\frac{\partial f_2}{\partial\dot{r}} & \frac{\partial f_2}{\partial\dot{\theta}} \\ \frac{\partial f_3}{\partial r} & \frac{\partial f_3}{\partial\theta} &\frac{\partial f_3}{\partial\dot{r}} & \frac{\partial f_3}{\partial\dot{\theta}} \\ \frac{\partial f_4}{\partial r} & \frac{\partial f_4}{\partial\theta} &\frac{\partial f_4}{\partial\dot{r}} & \frac{\partial f_4}{\partial\dot{\theta}} \end{array}\right] \right|_{r=0,\theta=\theta^*,\dot{r}=0,\dot{\theta}=0,F=F^*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3287a406e47f96caee26fb5d7e39129a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \frac{\partial f(\xi^*,\zeta^*)}{\partial\zeta} =\left.\left[\begin{array}{cccc} \frac{\partial f_1}{\partial F} \\ \frac{\partial f_2}{\partial F} \\ \frac{\partial f_3}{\partial F} \\ \frac{\partial f_4}{\partial F} \end{array}\right] \right|_{r=0,\theta=\theta^*,\dot{r}=0,\dot{\theta}=0,F=F^*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bab1bcd48b67405a9e0d85d026eac2ef_l3.png)
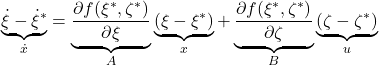
![Rendered by QuickLaTeX.com \underbrace{ \frac{d}{dt} \left[\begin{array}{c} r-r^* \\ \theta-\theta^* \\ \dot{r}-\dot{r}^* \\ \dot{\theta}-\dot{\theta}^* \end{array}\right] }_{\dot{x}}= \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & a_{32} & 0 & 0\\ 0 & a_{42} & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} r-r^* \\ \theta-\theta^* \\ \dot{r}-\dot{r}^* \\ \dot{\theta}-\dot{\theta}^* \end{array}\right] }_{x} +\underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ b_{32} \\ b_{42} \end{array}\right] }_{B} \underbrace{ (\dot{\zeta}-\dot{\zeta}^*) }_{u}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e1f883a4b1a3ed2618abc05e42a9c6ff_l3.png)
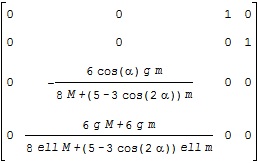
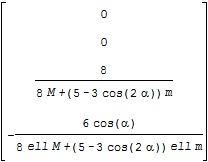
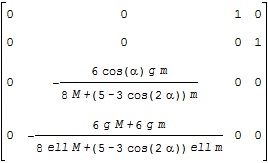
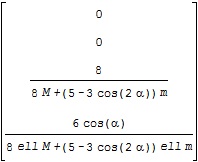
![Rendered by QuickLaTeX.com \begin{array}{lll} \underbrace{ \left[\begin{array}{cc} f_1(x_1,x_2)\\ f_2(x_1,x_2) \end{array}\right] }_{f(x)}\nonumber\\ \simeq \left[\begin{array}{cc} f_1(a_1,a_2)+\frac{\partial\,f_1(a_1,a_2)}{\partial\,x_1}(x_1-a_1)+\frac{\partial\,f_1(a_1,a_2)}{\partial\,x_2}(x_2-a_2)\\ f_2(a_1,a_2)+\frac{\partial\,f_2(a_1,a_2)}{\partial\,x_1}(x_1-a_1)+\frac{\partial\,f_2(a_1,a_2)}{\partial\,x_2}(x_2-a_2) \end{array}\right]\nonumber\\ = \underbrace{ \left[\begin{array}{cc} f_1(a_1,a_2)\\ f_2(a_1,a_2) \end{array}\right] }_{f(a)} + \underbrace{ \left[\begin{array}{cc} \frac{\partial f_1(a_1,a_2)}{\partial x_1}&\frac{\partial f_1(a_1,a_2)}{\partial x_2}\\ \frac{\partial f_2(a_1,a_2)}{\partial x_1}&\frac{\partial f_2(a_1,a_2)}{\partial x_2} \end{array}\right] }_{\frac{\partial\,f(a)}{\partial\,x}} \underbrace{ \left[\begin{array}{cc} x_1-a_1\\ x_2-a_2\nonumber \end{array}\right] }_{x-a}\nonumber \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-67d6279d41d4a2c86662d65aeca81a64_l3.png)
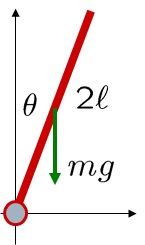
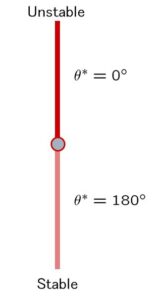
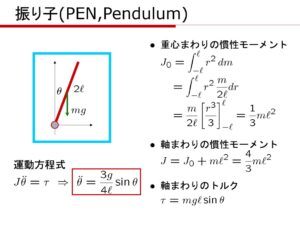
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} \dot{\theta}^* \\ \dot{\omega}^* \end{array}\right] }_{\dot{\xi}^*} = \underbrace{ \left[\begin{array}{c} \omega^* \\ \frac{3g}{4\ell}\sin\theta^* \end{array}\right] }_{f(\xi^*)} = \underbrace{ \left[\begin{array}{c} 0 \\ 0 \end{array}\right] }_{0} \ \Rightarrow\ \xi^* = \left[\begin{array}{c} \theta^* \\ \omega^* \end{array}\right] = \left[\begin{array}{c} 0 \\ 0 \end{array}\right] \,or\, \left[\begin{array}{c} \pi \\ 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cb697f6e9356b7da4dbf07362adaa686_l3.png)
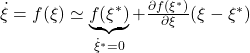
![Rendered by QuickLaTeX.com \displaystyle{ \frac{\partial f(\xi^*)}{\partial\xi}=\left.\left[\begin{array}{cc} \frac{\partial f_1}{\partial\theta} & \frac{\partial f_1}{\partial\omega} \\ \frac{\partial f_2}{\partial\theta} & \frac{\partial f_2}{\partial\omega} \end{array}\right] \right|_{\theta=\theta^*,\omega=0}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dcbf2bcb28e293a5f81e0e8bee5efa92_l3.png)
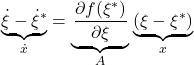
![Rendered by QuickLaTeX.com \underbrace{ \frac{d}{dt} \left[\begin{array}{c} \theta-\theta^* \\ \omega-\omega^* \end{array}\right] }_{\dot{x}}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ \frac{3g}{4\ell}\cos\theta^* & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \theta-\theta^* \\ \omega-\omega^* \end{array}\right] }_{x}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1112619eccc3155d42b3e7a0f78a9753_l3.png)