2026.1.5
「未分類」カテゴリーアーカイブ
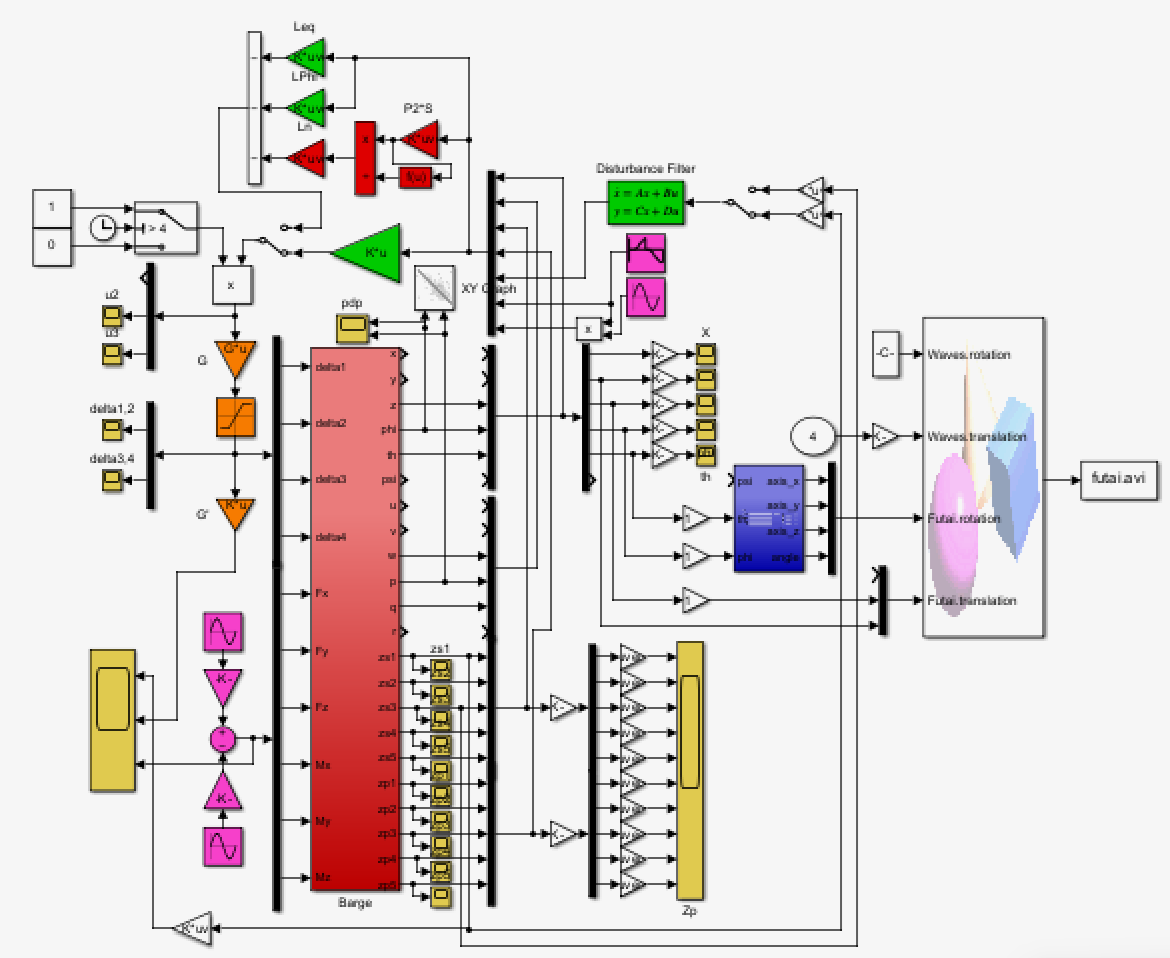
非線形シミュレーション(旧版)
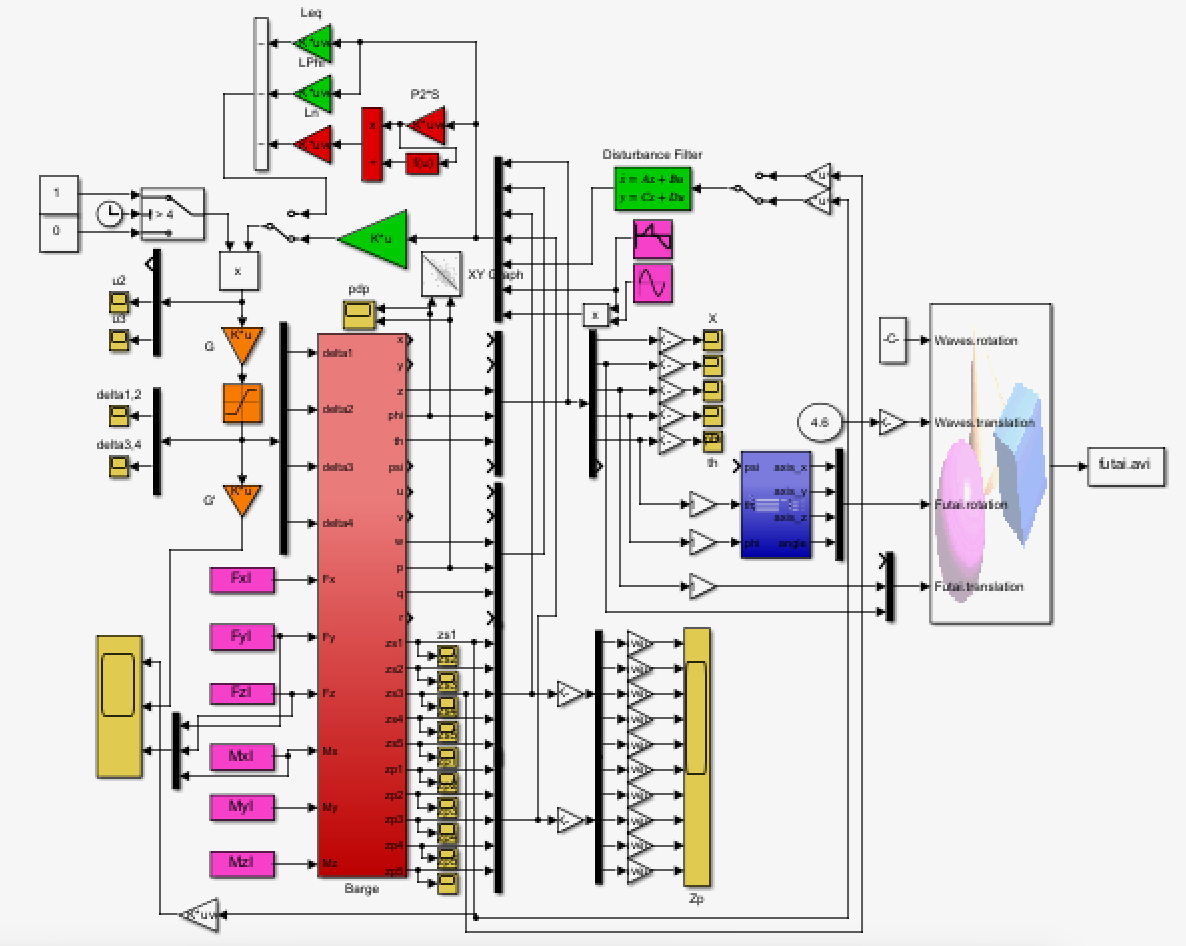
●制御対象(赤)
\left\{\begin{array}{l}
\dot{\vec x}=A(T_w){\vec x}+B(T_w)\vec{u}+B_w(T_w,\beta){\vec w}(T_w),\ {\vec x}(0)={\vec x}_0\\
{\vec y}_M=C_M{\vec x}\\
y=\underbrace{C_SC_M}_{C}{\vec x}
\end{array}\right.
●外乱信号(赤紫)
{\vec w}(T_w)=\left[\begin{array}{l}
H_w\sin\frac{2\pi}{T_w} t \\
H_w\cos\frac{2\pi}{T_w} t
\end{array}\right]
不規則波については時系列データを準備。
●外乱推定に用いる観測変数(緑)
y_d=C_d{\vec x}
主に制御点の縦変位を取る。
●外乱フィルタ(緑)
\dot{\hat{\vec x}}_d=A_d(T_w)\hat{{\vec x}}_d+B_d(T_w){y}_d,\ \hat{x}_d(0)=0
●非線形要素
-スラスタ伝達静特性:3次関数(V-F表)、入力電圧不感帯-1V~0V
-スラスタ伝達動特性:1次遅れ、時定数1/sqrt(50)、2/sqrt(50)、…
-スラスタ入力電圧リミッタ:±2.5V、±5V
●LQ制御/H∞制御
\vec{u}=-F(T_w)\vec{x}
●LQIM制御/H∞IM制御
\vec{u}=-F(T_w)\vec{x}-F_d(T_w)\hat{\vec{x}}_d
●SM制御
![]()
![]()
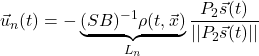
このとき、次の諸ケースについて、非線形シミュレーションを行ないます。ただし、短周期は![]() 、長周期は
、長周期は![]() とします。
とします。
| 制御方式 | 横波短周期 | 横波長周期 | 斜波短周期 | 斜波長周期 |
|---|---|---|---|---|
| LQ制御 | Case 4.1 | Case 4.2 | Case 4.3 | Case 4.4 |
| H∞制御 | Case 4.5 | Case 4.6 | Case 4.7 | Case 4.8 |
| SM制御 | Case 4.9 | Case 4.10 | Case 4.11 | Case 4.12 |
| LQIM制御 | Case 4.13 | Case 4.14 | Case 4.15 | Case 4.16 |
| H∞IM制御 | Case 4.17 | Case 4.18 | Case 4.19 | Case 4.20 |
| 制御方式 | 不規則波1 | 不規則波2 | 時間遅れ | 入力電圧制限 |
|---|---|---|---|---|
| LQ制御 | Case 5.1 | Case 5.2 | Case 5.3 | Case 5.4 |
| H∞制御 | Case 5.5 | Case 5.6 | Case 5.7 | Case 5.8 |
| SM制御 | Case 5.9 | Case 5.10 | Case 5.11 | Case 5.12 |
| LQIM制御 | Case 5.13 | Case 5.14 | Case 5.15 | Case 5.16 |
| H∞IM制御 | Case 5.17 | Case 5.18 | Case 5.19 | Case 5.20 |
LQ制御
Case 4.1(横波、短周期規則波) Case 4.2(横波、長周期規則波)
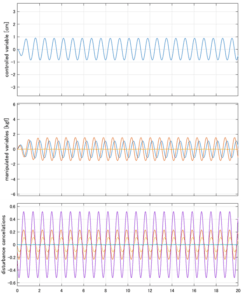
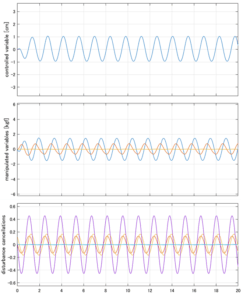
Case 4.3(斜波、短周期規則波) Case 4.4(斜波、長周期規則波)
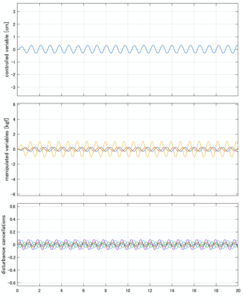
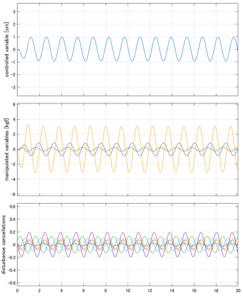
Case 5.1(横波、不規則波1)
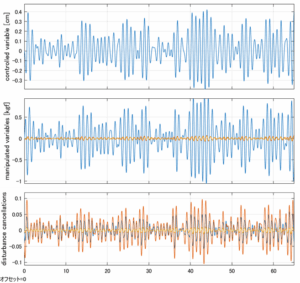
Case 5.2(横波、不規則波2)
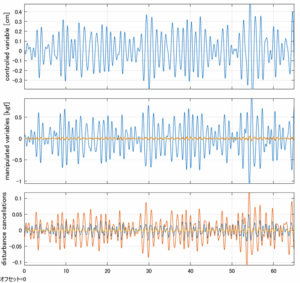
Case 5.3(横波、時間遅れ1秒) Case 5.4(横波、リミッタ2.5V)
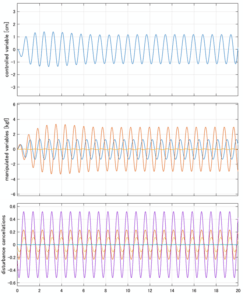
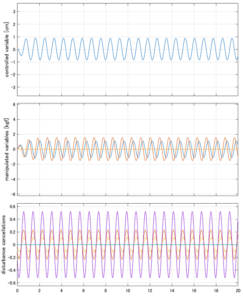
H∞制御
Case 4.5(横波、短周期規則波) Case 4.6(横波、長周期規則波)
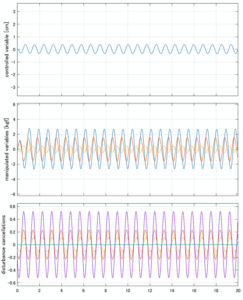
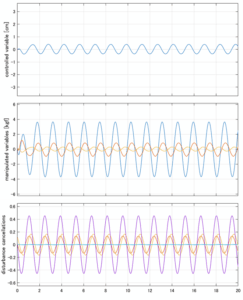
Case 4.7(斜波、短周期規則波) Case 4.8(斜波、長周期規則波)
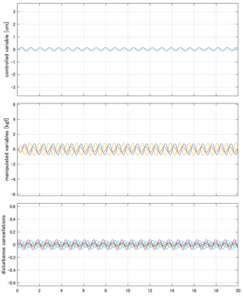
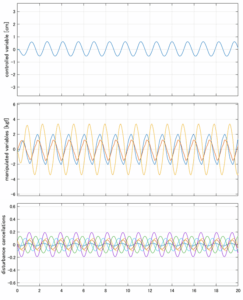
Case 5.5(横波、不規則波1)
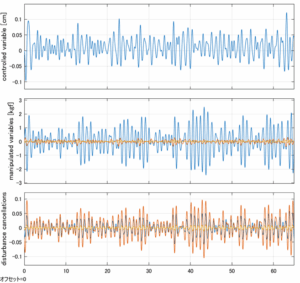
Case 5.6(横波、不規則波2)
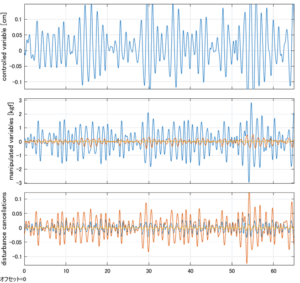
Case 5.7(横波、時間遅れ1秒) Case 5.8(横波、リミッタ2.5V)
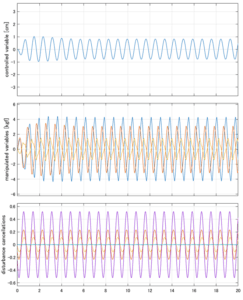
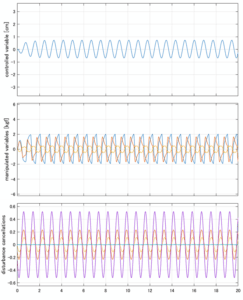
SM制御
Case 4.9(横波、短周期規則波)
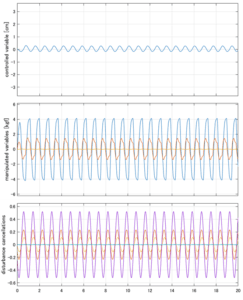
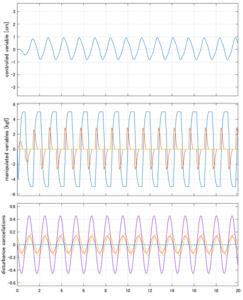
Case 4.11(斜波、短周期規則波) Case 4.12(斜波、長周期規則波)
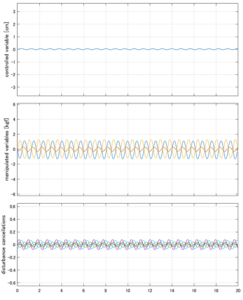
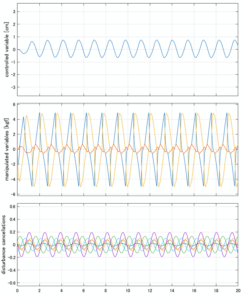
Case 5.9(横波、不規則波1)
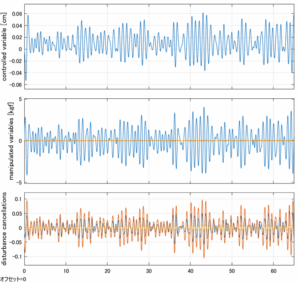
Case 5.10(横波、不規則波2)
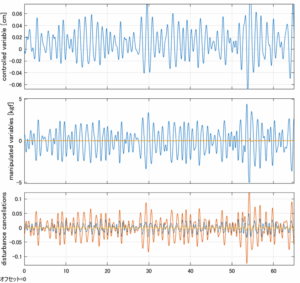
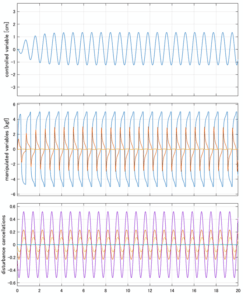
Case 5.11(横波、時間遅れ1秒) Case 5.12(横波、リミッタ2.5V)
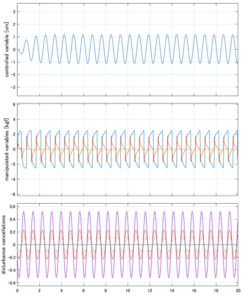
LQIM制御
Case 4.13(横波、短周期規則波) Case 4.14(横波、長周期規則波)
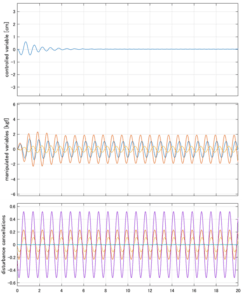
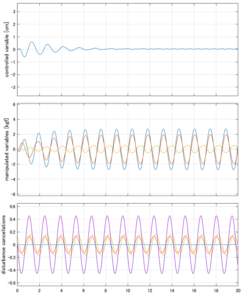
Case 4.15(斜波、短周期規則波) Case 4.16(斜波、長周期規則波)
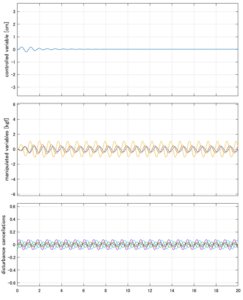
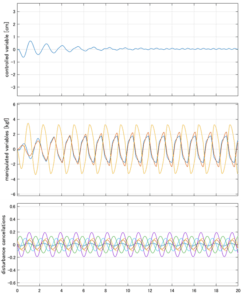
Case 5.13(横波、不規則波1)
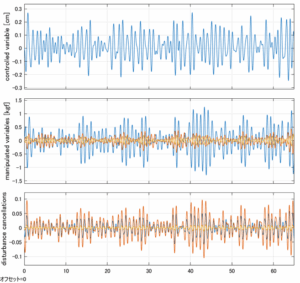
Case 5.14(横波、不規則波2)
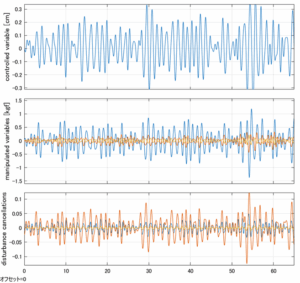
Case 5.15(横波、時間遅れ) Case 5.16()
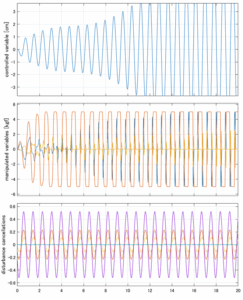
H∞IM制御
Case 4.17(横波、短周期規則波) Case 4.18(横波、長周期規則波)
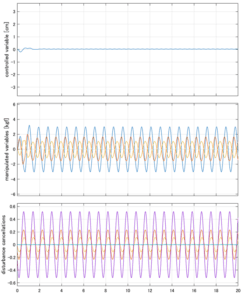
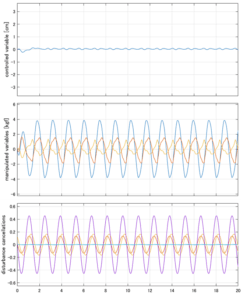
Case 4.19(斜波、短周期規則波) Case 4.20(斜波、長周期規則波)
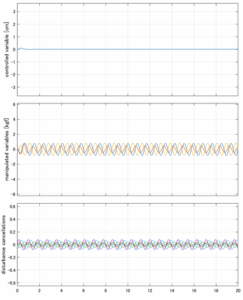
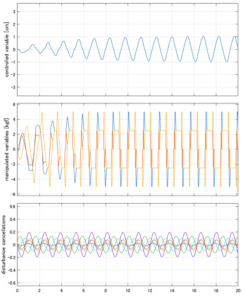
Case 5.17(横波、不規則波1)
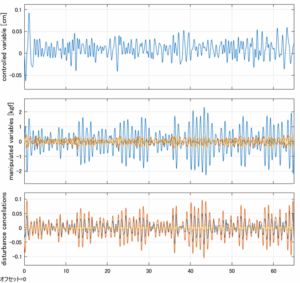
Case 5.18(横波、不規則波2)
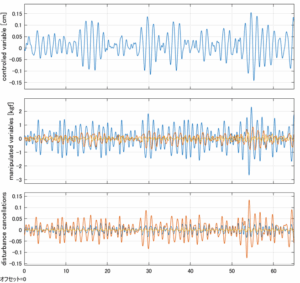
Case 5.19(横波、時間遅れ) Case 5.20()
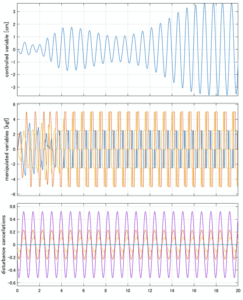
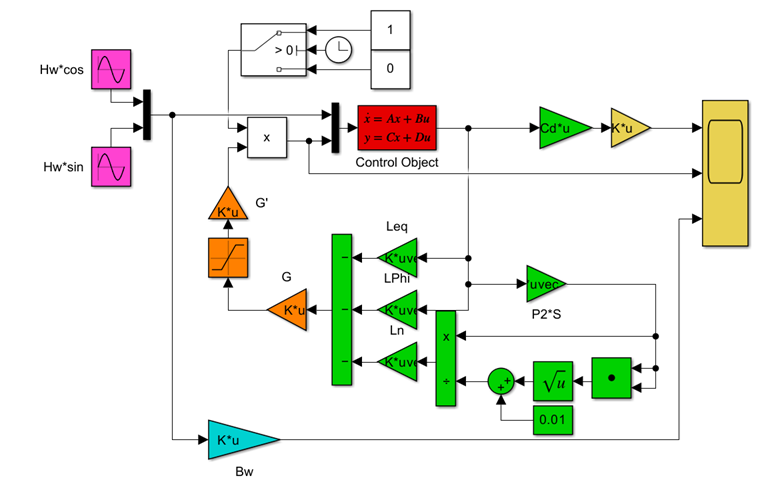
SM制御(旧版)
●制御対象(赤)
\left\{\begin{array}{l}
\dot{\vec x}=A(T_w){\vec x}+B(T_w)\vec{u}+B_w(T_w,\beta){\vec w},\ {\vec x}(0)={\vec x}_0\\
{\vec y}_M=C_M{\vec x}\\
y=\underbrace{C_SC_M}_{C}{\vec x}
\end{array}\right.
●外乱信号(赤紫)
{\vec w}=\left[\begin{array}{l}
H_w\sin\frac{2\pi}{T_w} t \\
H_w\cos\frac{2\pi}{T_w} t
\end{array}\right]
●SM制御則
![]()
![]()
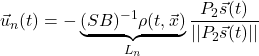
このとき、次の12ケースについて、線形シミュレーションを行ないます。ただし、短周期は![]() 、長周期は
、長周期は![]() とします。
とします。
| モデル/制御 | 横波短周期 | 横波長周期 | 斜波短周期 | 斜波長周期 |
|---|---|---|---|---|
| 2次系/SM | Case 3.1 | Case 3.2 | Case 3.3 | Case 3.4 |
| 4次系/SM | Case 3.5 | Case 3.6 | Case 3.7 | Case 3.8 |
| 6次系/SM | Case 3.9 | Case 3.10 | Case 3.11 | Case 3.12 |
|
|
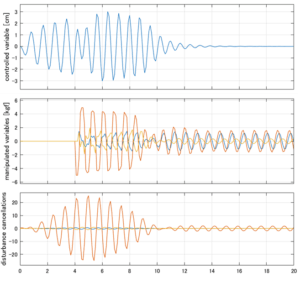
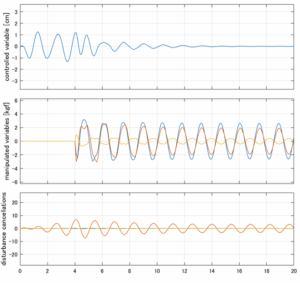
以下に、シミュレーション結果を示します。各ケースについて左図がSM制御系の応答を示しています。左図上段は制御点の応答[cm]、左図中段は操作入力[kgf]、左図下段は波浪力[kgf]を示しています。4秒までは制御なしで、4秒以降が制御ありです。制御点は横波・斜波とも右舷船首S1を取っています(横波の場合、右舷制御点の区別はありません)。また操作入力には5Vのリミッタを掛けています。
2次モデルに対するSM制御
Case 3.1(横波、短周期規則波) Case 3.1(横波、長周期規則波)
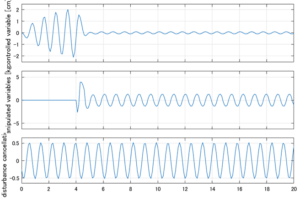
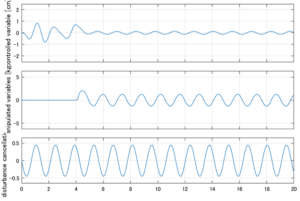
Case 3.3(斜波、短周期規則波) Case 3.4(斜波、長周期規則波)
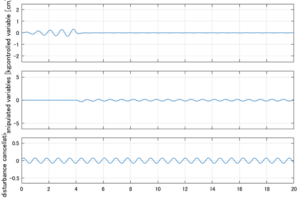
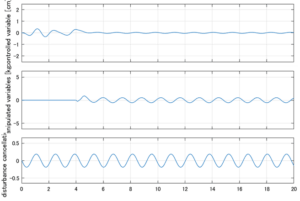
4次モデルに対するSM制御
Case 3.5(横波、短周期規則波) Case 3.6(横波、長周期規則波)
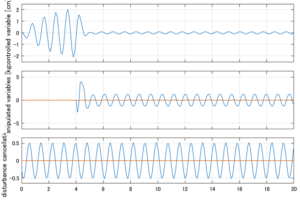
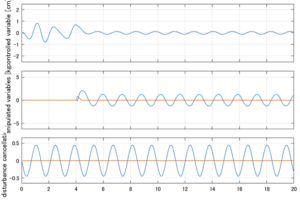
Case 3.7(斜波、短周期規則波) Case 3.8(斜波、長周期規則波)
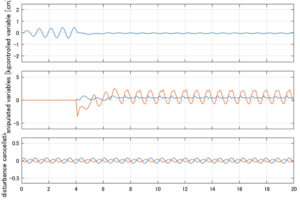
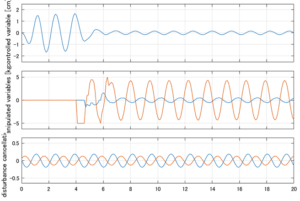
6次モデルに対するSM制御
Case 3.9(横波、短周期規則波) Case 3.10(横波、長周期規則波)
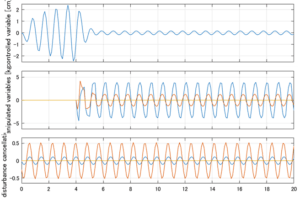
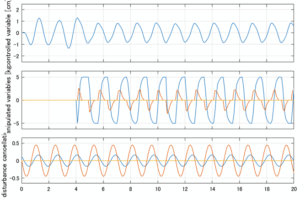
Case 3.11(斜波、短周期規則波) Case 3.12(斜波、長周期規則波)
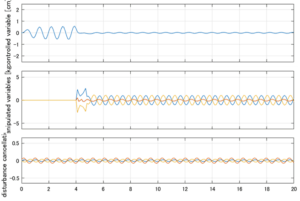
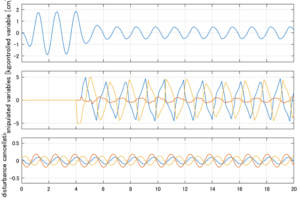
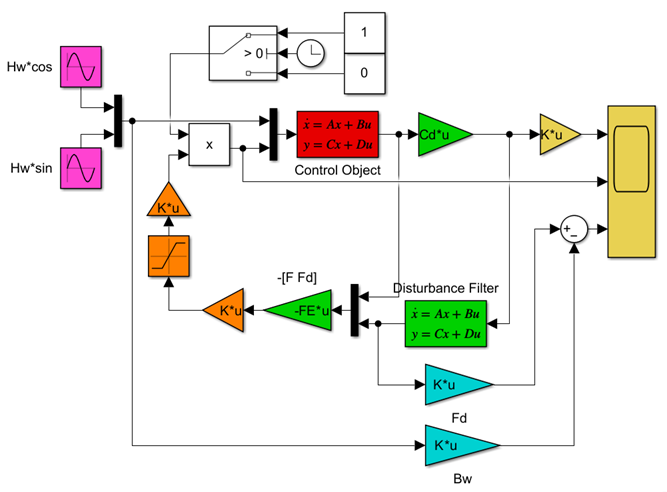
LQIM制御/H∞IM制御(旧版)
●制御対象(赤)
\left\{\begin{array}{l}
\dot{\vec x}=A(T_w){\vec x}+B(T_w)\vec{u}+B_w(T_w,\beta){\vec w},\ {\vec x}(0)={\vec x}_0\\
{\vec y}_M=C_M{\vec x}\\
y=\underbrace{C_SC_M}_{C}{\vec x}
\end{array}\right.
●外乱信号(赤紫)
{\vec w}=\left[\begin{array}{l}
H_w\sin\frac{2\pi}{T_w} t \\
H_w\cos\frac{2\pi}{T_w} t
\end{array}\right]
ここで、![]() とする。
とする。
●外乱推定に用いる観測変数(緑)
y_d=C_d{\vec x}
これは主に制御点の縦変位を取る。
●外乱フィルタ(緑)
\dot{\hat{\vec x}}_d=A_d(T_w)\hat{{\vec x}}_d+B_d(T_w){y}_d,\ \hat{x}_d(0)=0
●安定化制御則(緑)
\vec{u}=-F(T_w)\vec{x}-F_d(T_w)\hat{\vec{x}}_d
●推力配分(橙)
![]() は制御目的を達成するための望ましい
は制御目的を達成するための望ましい![]() であるが、これは4つのスラスタに次式で配分する。
であるが、これは4つのスラスタに次式で配分する。
\underbrace{\left[\begin{array}{c}F_1\\F_2\\F_3\\F_4\end{array}\right]}_{\vec F}=
\underbrace{\frac{1}{4}\left[\begin{array}{rrr} 1 & 1 & -1 \\ 1 & 1 & 1 \\ 1 & -1 & 1\\1 & -1 & -1 \end{array}\right]}_{G^\dag}
\underbrace{\left[\begin{array}{c}F_z\\F_\phi\\F_\theta\end{array}\right]}_{\vec\tau}
●推力制限(橙)
その際、次の制約が課される。
F_{min}\le F_k\le F_{max}\quad(k=1,2,3,4)
上のシミュレータは、この制約を考慮したものとなっている。ここでは、F_{max}=5[kgf]、F_{min}=-5[kgf]を用いる(要チェック)。
●留意点
制約を受けた推力は次式で駆動力に変換されるが、推力制限がある場合は設計した駆動力が働かないので注意が必要である。
\underbrace{\left[\begin{array}{c}F_z\\F_\phi\\F_\theta\end{array}\right]}_{\vec\tau}=
\underbrace{\left[\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & 1 & -1 & -1\\ -1 & 1 & 1 & -1 \end{array}\right]}_{G}
\underbrace{\left[\begin{array}{c}F_1\\F_2\\F_3\\F_4\end{array}\right]}_{\vec F}
このとき、次の16ケースについて、上のシミュレータを用いてシミュレーションを行なう。ただし、短周期は![]() 、長周期は
、長周期は![]() とする。
とする。
| モデル/制御 | 横波短周期 | 横波長周期 | 斜波短周期 | 斜波長周期 |
|---|---|---|---|---|
| 2次系/LQIM | Case 2.1 | Case 2.2 | Case 2.3 | Case 2.4 |
| 4次系/LQIM | Case 2.5 | Case 2.6 | Case 2.7 | Case 2.8 |
| 6次系/LQIM | Case 2.9 | Case 2.10 | Case 2.11 | Case 2.12 |
| 6次系/H∞IM | Case 2.13 | Case 2.14 | Case 2.15 | Case 2.16 |
|
|
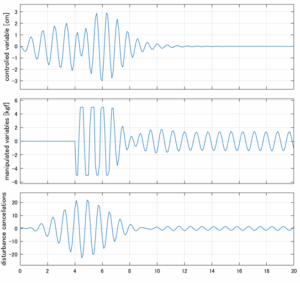
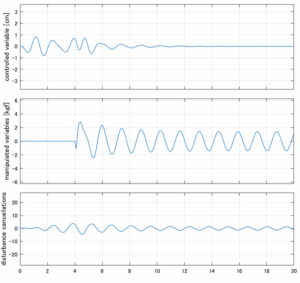
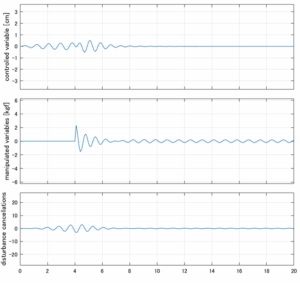
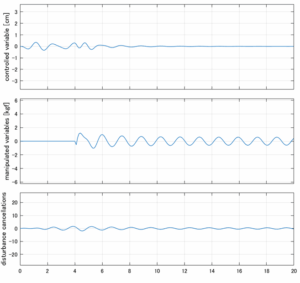
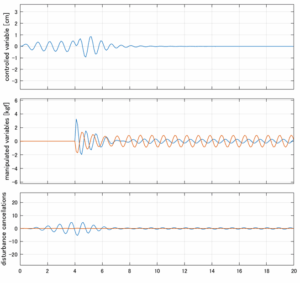
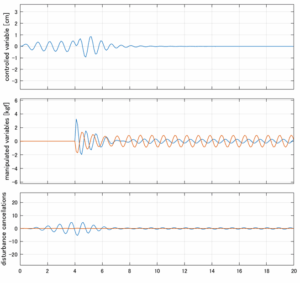
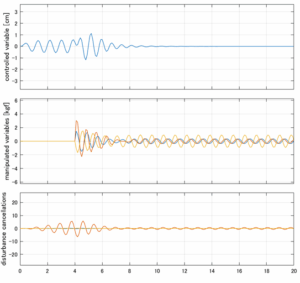
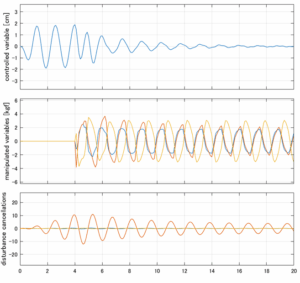
以下に、各ケースについてLQ制御系/H∞制御系の応答とゲイン線図を示す。前者の上段は制御点の応答[cm]、中段は操作入力[kgf]、下段は波浪外力[kgf]を示している。閉ループ系では
\dot{\vec x}=(A(T_w)-B(T_w)F(T_w)){\vec x}\underbrace{-B(T_w)F_d(T_w)\hat{\vec{x}}_d+B_w(T_w,\beta){\vec w}}_{相殺?}
が成り立つと思われる。左辺第2項(外乱推定項)と第3項(外乱項)が相殺するかどうかを下段で確認している。4秒までは制御なしで、4秒以降が制御ありの応答。制御点は横波・斜波とも右舷船首S1を取っている(横波の場合、右舷制御点の区別はない)。
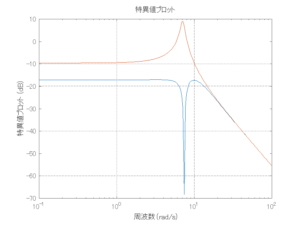
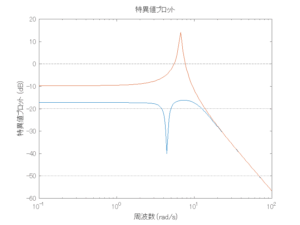
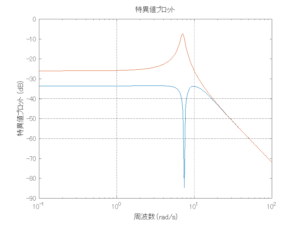
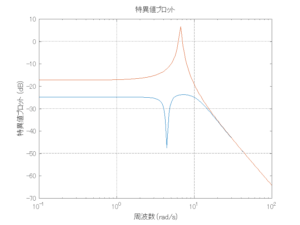
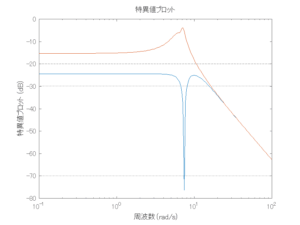
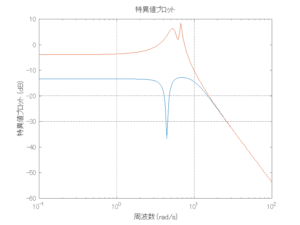
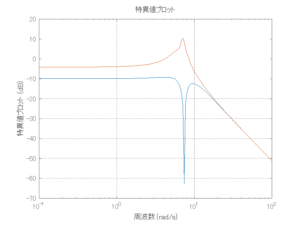
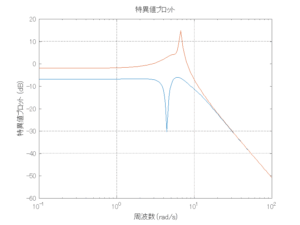
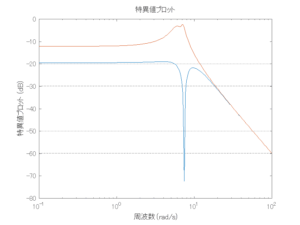
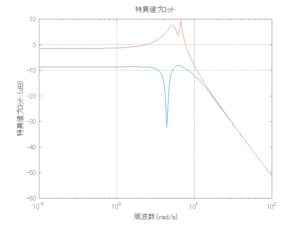
●留意点
外乱から着目する制御点までのゲイン線図は、LQIM制御系の場合、波周波数においてピンポイントで低減され、H∞IM制御系の場合、波周波数近傍で低減されている。
2次モデルに対するLQIM制御
Case 2.1(横波、短周期規則波) Case 2.2(横波、長周期規則波)
Case 2.3(斜波、短周期規則波) Case 2.4(斜波、長周期規則波)
4次モデルに対するLQIM制御
Case 2.5(横波、短周期規則波) Case 2.6(横波、長周期規則波)
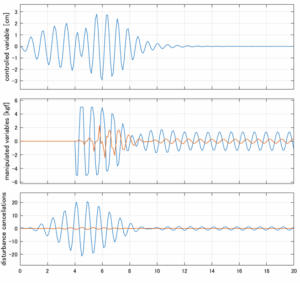
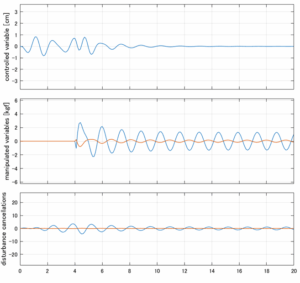
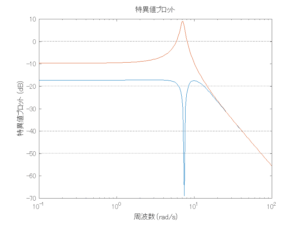
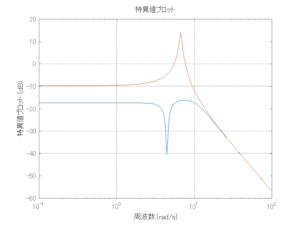
Case 2.7(斜波、短周期規則波) Case 2.8(斜波、長周期規則波)
6次モデルに対するLQIM制御
Case 2.9(横波、短周期規則波) Case 2.10(横波、長周期規則波)
Case 2.11(斜波、短周期規則波) Case 2.12(斜波、長周期規則波)
6次モデルに対するH∞IM制御
Case 2.13(横波、短周期規則波) Case 2.14(横波、長周期規則波)
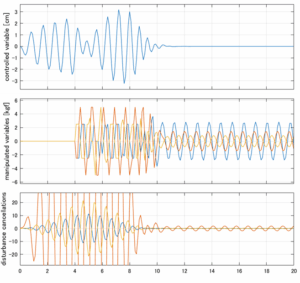
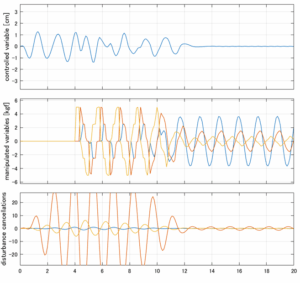
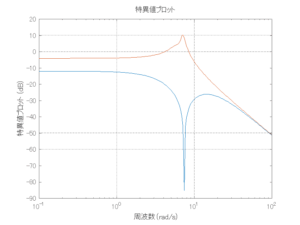
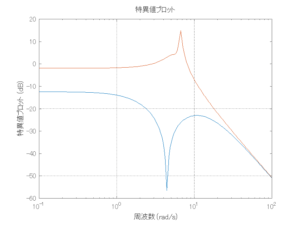
Case 2.15(斜波、短周期規則波) Case 2.16(斜波、長周期規則波)
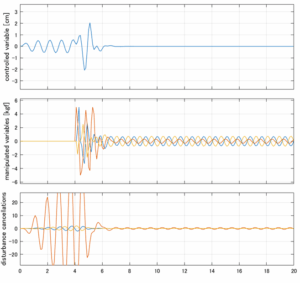
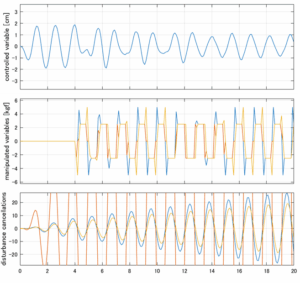
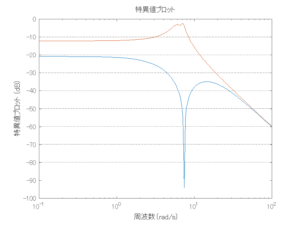
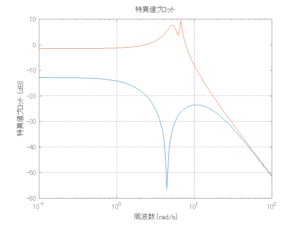
Case 2.16コメント
この場合だけ制御性能が劣化しているが、操作入力のリミッタを5Vから少し緩めたり、制御動作を4秒からでなく少し早めたりすれば、Case 2.13/14/15と同等になる。
補遺A
| OptSeq |
|
設備を増設した場合
| OptSeq |
|
次船を含めた場合
| OptSeq |
|
リスケの手法
リスケアクティビティの分類
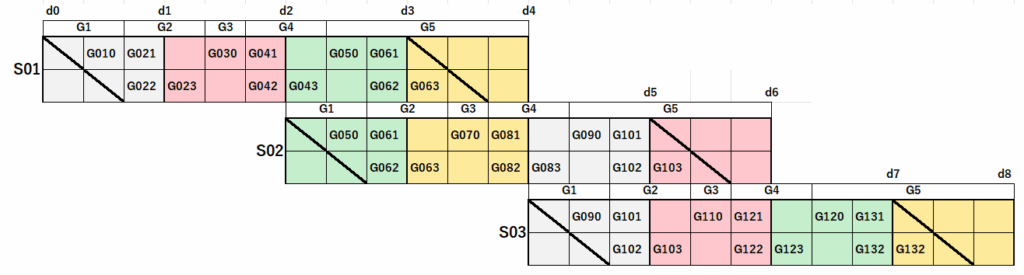

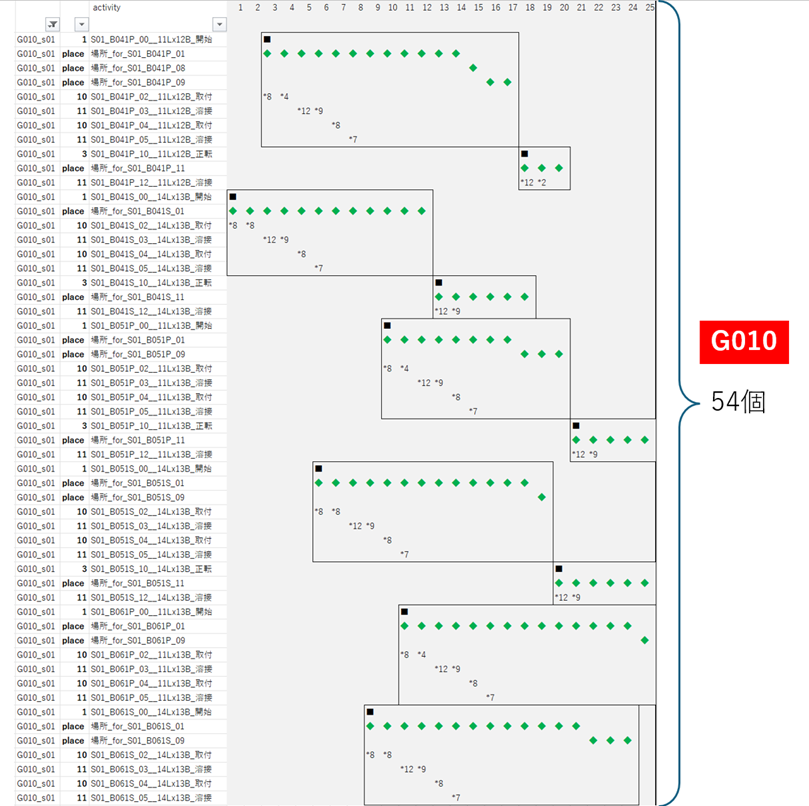
G010
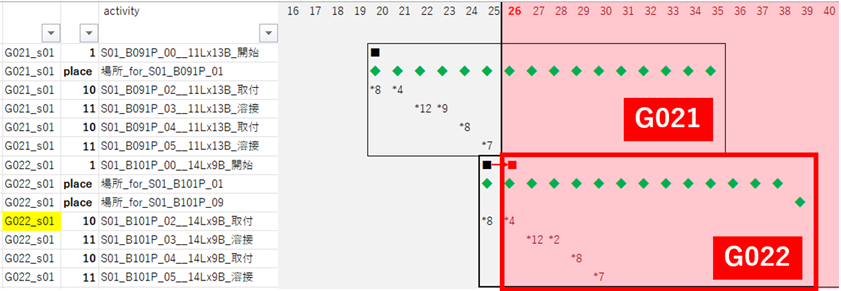
G021
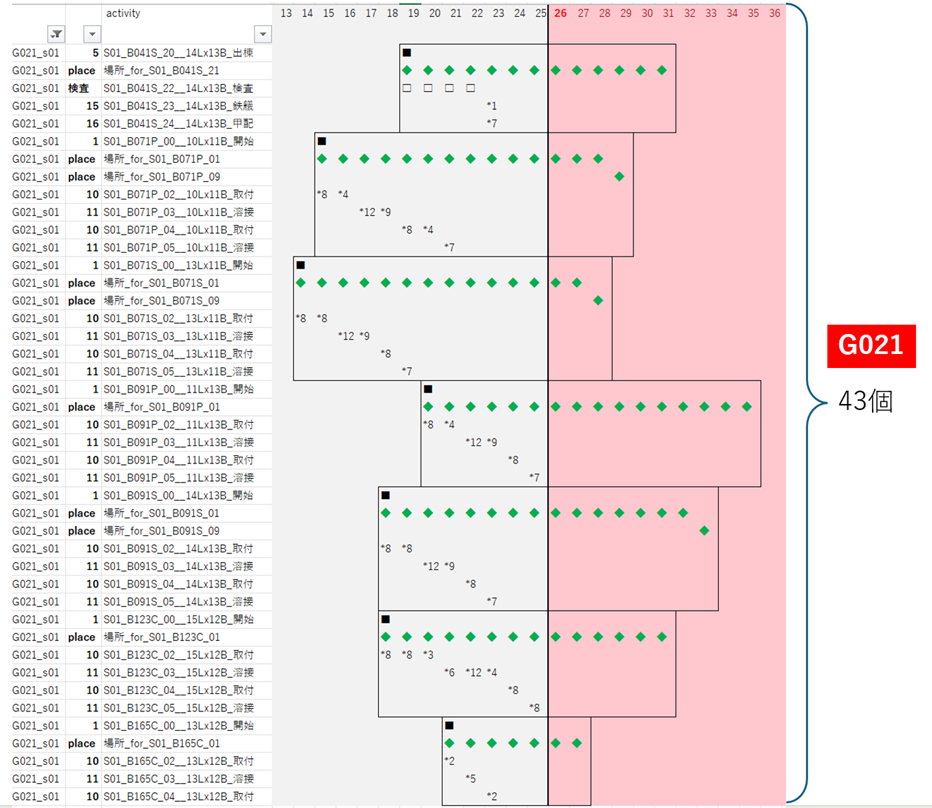
G022
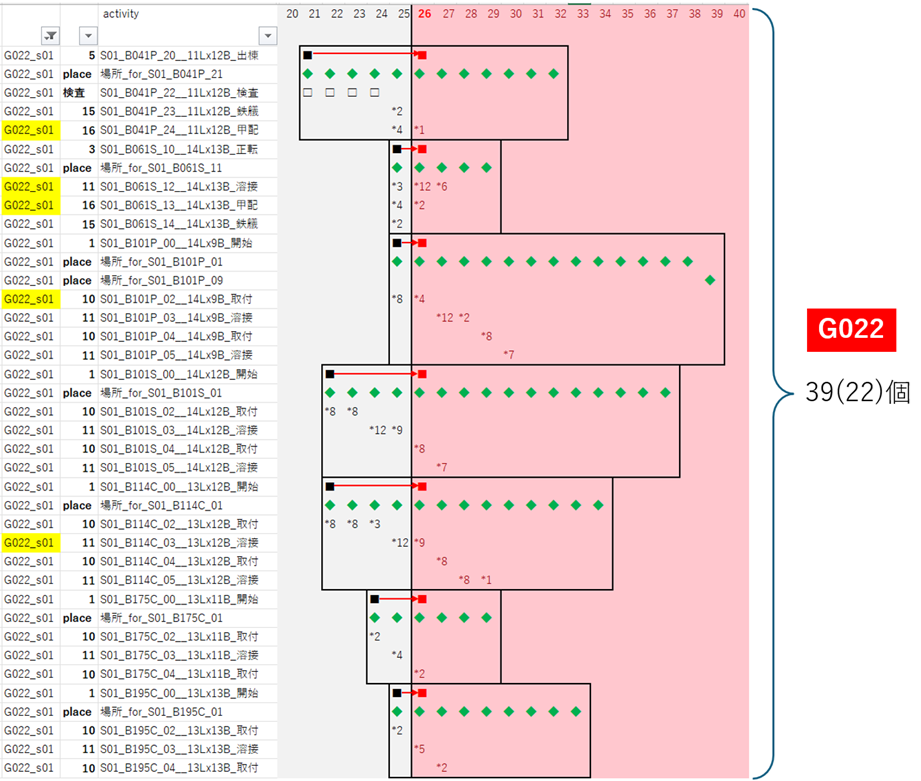
|
|
|
|
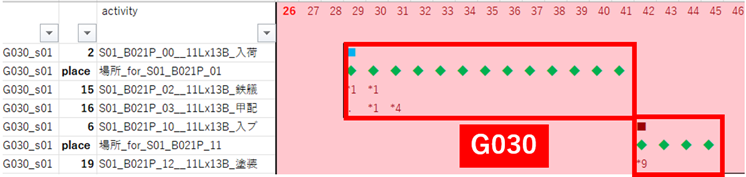
G030
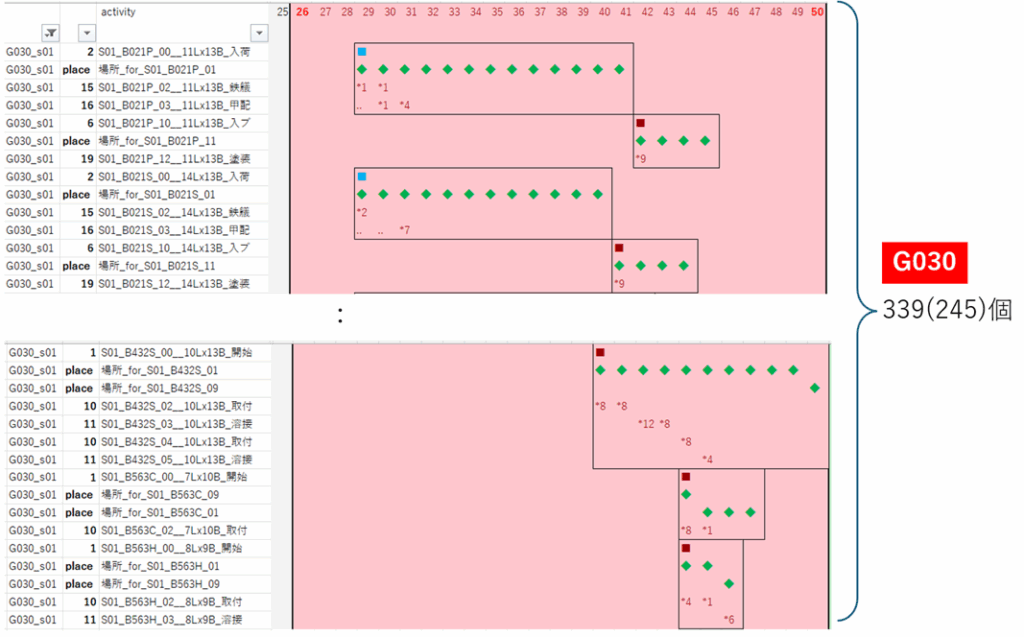
|
|
G041
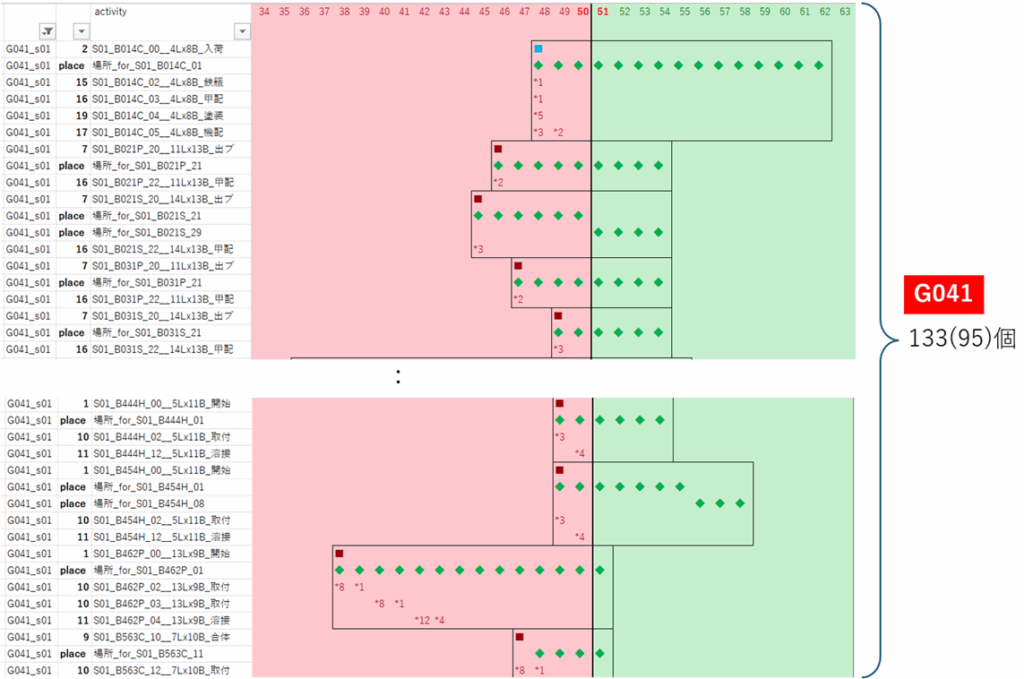
|
|
|
|
G042
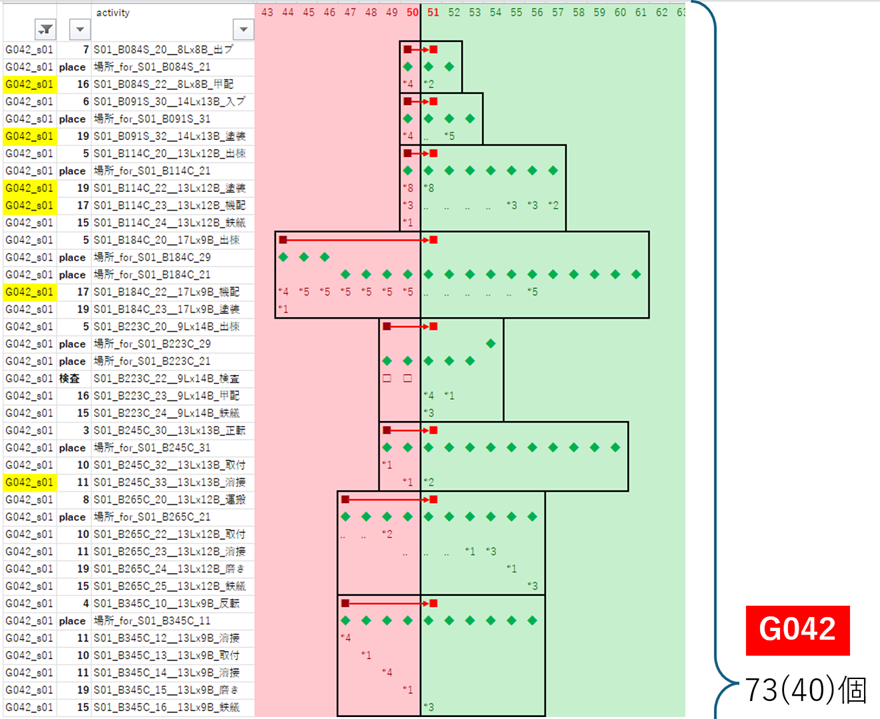
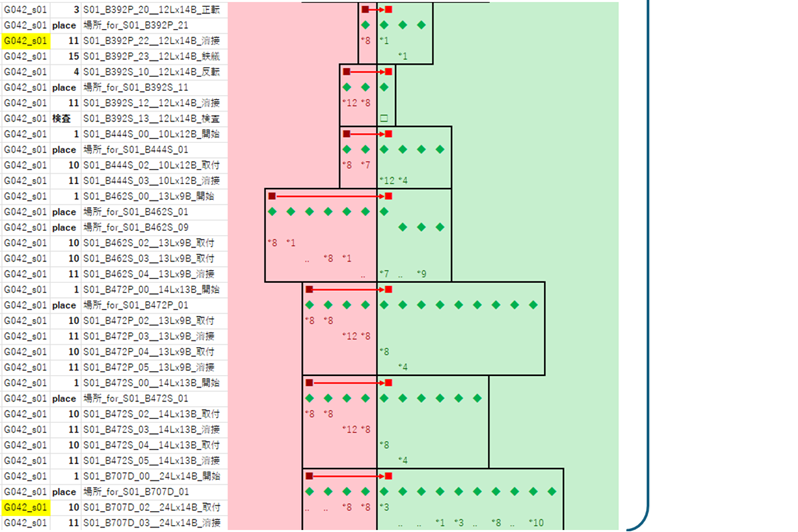
|
|
|
|
|
|
rcpsp71.py
|
|
|
|
|
|
|
|
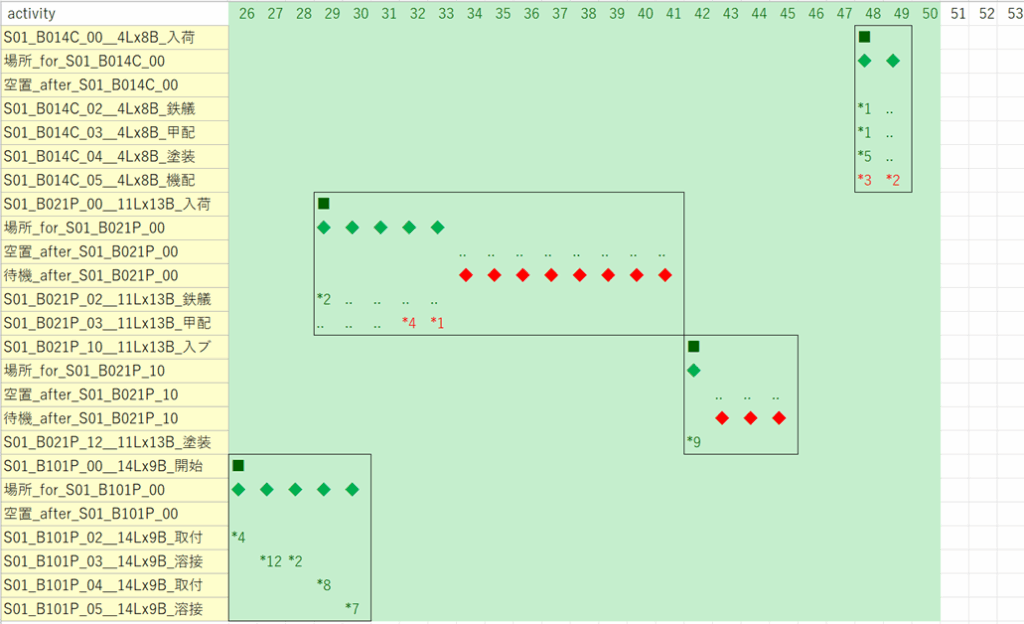
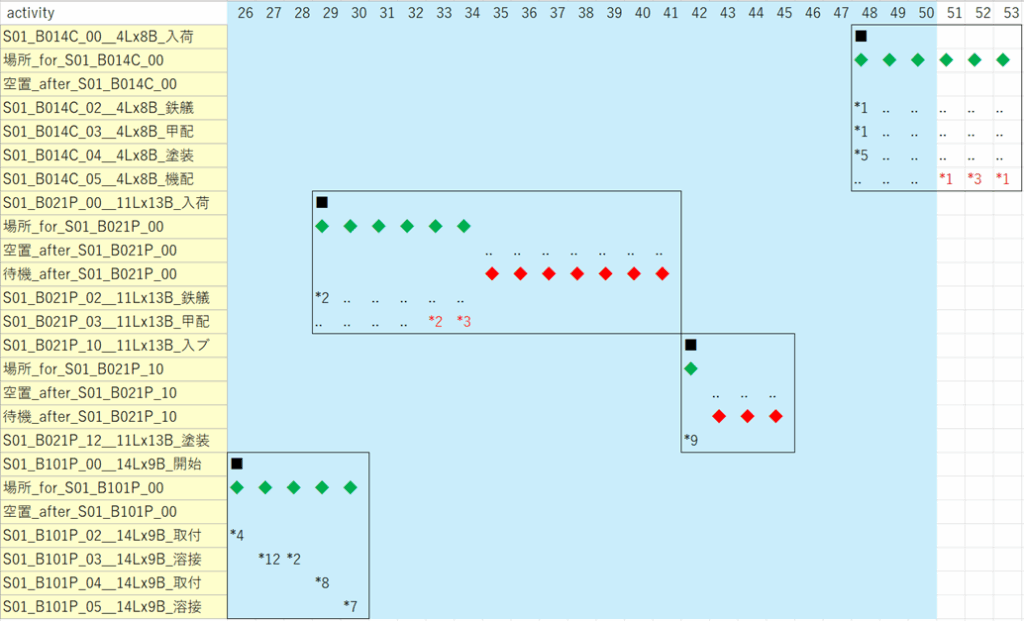
補遺6
| OptSeq |
|
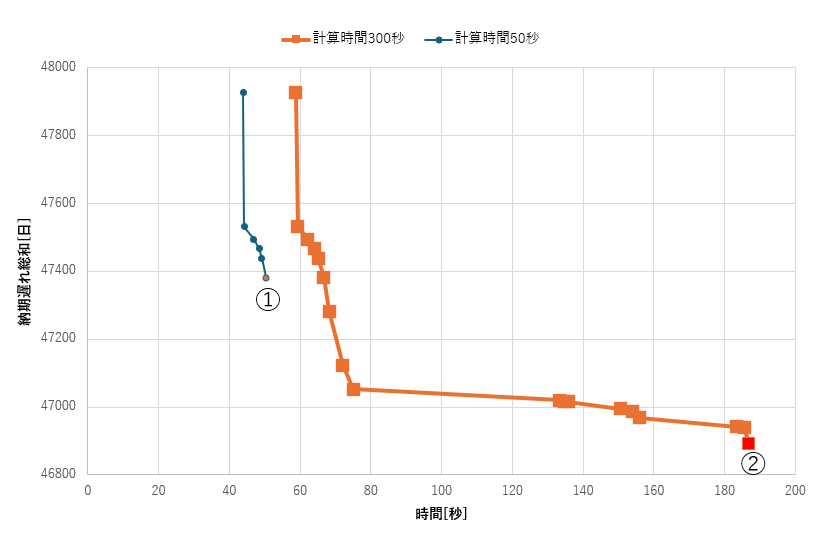
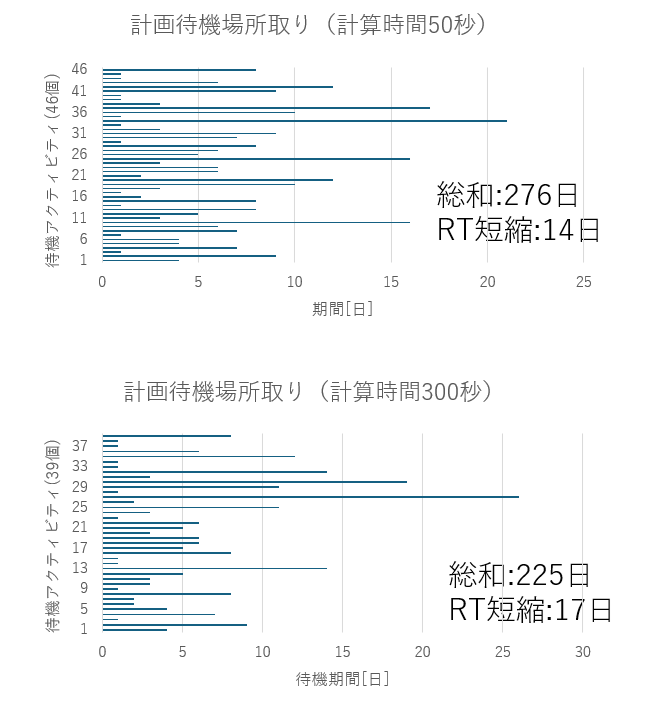
同時計画(点) Step1 収束過程はoptseq_output.txtに次のように記録されています。 同時計画(点) Step2 収束過程はoptseq_output.txtに次のように記録されています。 同時計画(面)同時計画の検討
001
002
003
004
005
006
007
008
009
010
011
012
013
014
015
016
017
018
019
020
021
022
023
024
025
026
027
028
029
030
031
032
033
034
035
036
037
038
039
040
041
042
043
044
045
046
047
048
049
050
051
052
053
054
055
056
057
058
059
#rcpsp63.py プル型同時計画(点)
from optseq import *
import math
#=======================================================================
prob=Model()
CS=["CS","CC","SS","SC"]
#=======================================================================
#リソースの定義(A造船所)
file_path = 'rcpsp_shipyard_A.txt'
with open(file_path, 'r', encoding='utf-8') as file:
prog=file.read()
exec(prog)
#=======================================================================
#データセットの定義(S01)
# data_BC1, data_BC2, data_BC3, data_BC4, data_BC5, data_BC6, data_BC7
file_path = 'rcpsp_dataset_S01.txt'
with open(file_path, 'r', encoding='utf-8') as file:
prog=file.read()
exec(prog)
#=======================================================================
data={}
data.update(data_BC1);
data.update(data_BC2);
data.update(data_BC3);
data.update(data_BC4);
data.update(data_BC5);
data.update(data_BC6);
data.update(data_BC7);
#-----
def extact(data):
w=[]
for i in data.keys():
if data[i][1]>=0: w.append(i)
return w
#-----
idata_BC1=extact(data_BC1)
idata_BC2=extact(data_BC2)
idata_BC3=extact(data_BC3)
idata_BC4=extact(data_BC4)
idata_BC5=extact(data_BC5)
idata_BC6=extact(data_BC6)
idata_BC7=extact(data_BC7)
idata=idata_BC1+idata_BC2+idata_BC3+idata_BC4+idata_BC5+idata_BC6+idata_BC7
print(len(idata))
#=======================================================================
def L1L2B1B2lb(R,data,i,j,no):
no1=data[i][j][no][0]; #j=6,7
L=R[no1][1]; B=R[no1][2];
l=math.floor(data[i][8][0]); b=math.floor(data[i][8][1]);
L1=data[i][j][no][1]; L2=data[i][j][no][2];
if L1<0: l=l-abs(L1); L1=0;
if L2>L: l=l-abs(L2-L); L2=L;
B1=data[i][j][no][3]; B2=data[i][j][no][4];
if B1<0: b=b-abs(B1); B1=0
if B2>B: b=b-abs(B2-B); B2=B;
ll=L2-L1; bb=B2-B1;
if L2-L1>l: ll=l
if B2-B1>b: bb=b
return [no1,L1,L2,B1,B2,ll,bb]
060
061
062
063
064
065
066
067
068
069
070
071
072
073
074
075
076
077
078
079
080
081
082
083
084
085
086
087
088
089
090
091
092
093
094
095
096
097
098
099
100
101
102
103
104
105
111
112
113
114
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
211
212
213
214
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
#=======================================================================
#iwhich=3 #プル型同時計画Step1: 作業の場所取りは実績ピンポイント
iwhich=4 #プル型同時計画Step2: 待機の場所取りは面全体
if iwhich in [3,4]:
#=======================================================================
if iwhich==3 : wplace=[] #計画上の待機なし
else: wplace=idata #計画上の待機あり
#=======================================================================
#[3.1]作業の定義
#=======================================================================
act={}
print("*** pull [3,4] ***")
for i in idata:
act[i]=prob.addActivity(data[i][0],duedate=98,backward=True)
# print("*** push" ***)
# for i in idata:
# act[i]=prob.addActivity(data[i][0])
#=======================================================================
#[3.2]先行制約
#=======================================================================
for i in idata:
for iw in [0,1,2,3,4]:
if data[i][4][iw] in idata:
prob.addTemporal(act[i],act[data[i][4][iw]],\
tempType=CS[data[i][5][iw][0]], delay=int(data[i][5][iw][1]))
#-----日程固定
for i in idata:
# 0搭載, 2入荷, 6入ブ, 7出ブ, 9合体, 1開始, 3正, 4反, 5出棟, 8運搬,
# if data[i][1] in [0,2,9]:
if data[i][1] in [0,2,6,7,9]:
# if data[i][1] in [0,1,2,3,4,5,6,7,8,9]:
prob.addTemporal("source",act[i],tempType="SS",delay= data[i][3])
prob.addTemporal(act[i],"source",tempType="SS",delay=-data[i][3])
#=======================================================================
#[3.3]資源制約(配員)
#=======================================================================
mode={}
wno1=0;wno2=0;wno3=0;wno4=0;wno5=0;wno6=0;wno7=0
for i in idata:
#10 F #11 W #12 C #13 CC #15 鉄艤 #16 甲配 #17 機配 #18 内塗 #19 外塗
if data[i][1] in [10,12,11,13,15,16,17,18,19]:
hours=10
n=math.ceil(data[i][9]/hours) #1人で何日かかるか
mode[i]=Mode("mode["+i+"]",duration=n)
mode[i].addBreak(0,"inf",maxtime=10)
if data[i][1] in [10,12]: #取付28人
mode[i].addResource(res1W[1],{(0,n):hours})
if n>7 : mode[i].addParallel(1,n,8)
else: mode[i].addParallel(1,n,4)
wno1+=1
elif data[i][1] in [11,13]: #溶接43人
mode[i].addResource(res1W[2],{(0,n):hours})
if n>11 : mode[i].addParallel(1,n,12)
else: mode[i].addParallel(1,n,8)
wno2+=1
elif data[i][1] in [15]: #鉄艤装5人
mode[i].addResource(res1W[4],{(0,n):hours})
if n>2 : mode[i].addParallel(1,n,5)
else: mode[i].addParallel(1,n,3)
wno3+=1
elif data[i][1] in [16]: #甲板配管7人
mode[i].addResource(res1W[5],{(0,n):hours})
if n>6 : mode[i].addParallel(1,n,7)
else: mode[i].addParallel(1,n,4)
wno4+=1
elif data[i][1] in [17]: #機関配管5人
mode[i].addResource(res1W[6],{(0,n):hours})
if n>14: mode[i].addParallel(1,n,5)
else: mode[i].addParallel(1,n,3)
wno5+=1
elif data[i][1] in [18]: #塗装12人
mode[i].addResource(res1W[3], {(0,n):hours})
if n>8 : mode[i].addParallel(1,n,9)
else: mode[i].addParallel(1,n,8)
wno6+=1
elif data[i][1] in [19]: #塗装12人
mode[i].addResource(res1W[3], {(0,n):hours})
if n>3 : mode[i].addParallel(1,n,8)
else: mode[i].addParallel(1,n,4)
wno6+=1
act[i].addModes(mode[i])
# 0搭載, 1開始, 2入荷, 3正, 4反, 5出棟, 6入ブ, 7出ブ, 8運搬, 9合体; 14ダミー
else:
mode[i]=Mode("mode["+i+"]",duration=data[i][2])
act[i].addModes(mode[i])
print(wno1,wno2,wno3,wno4,wno5,wno6)
#=======================================================================
#[3.4]資源制約(作業場所)
#=======================================================================
# 0搭載, 1開始, 2入荷, 3正, 4反, 5出棟, 6入ブ, 7出ブ, 8運搬, 9合体,
ww={}
for i in idata:
if data[i][1] in [1,2,3,4,5,6,7,8,9]:
for iw in [1,2,3,4]:
j=data[i][4][iw] #枝iwの後続作業ID
if j!="0":
#シリアルな後続は飛ばす
while data[j][8]==0: j=data[j][4][0]
ww[i,iw]=j
#----- 作業場所
d_act={}
d_mode={}
for i in idata:
if data[i][1] in [1,2,3,4,5,6,7,8,9] and data[i][6]!=0:
d_act[i]=prob.addActivity("場所_for_"+i)
for no in range(len(data[i][6])):
w=L1L2B1B2lb(R,data,i,6,no)
no1,L1,L2,B1,B2,l,b=w[0],w[1],w[2],w[3],w[4],w[5],w[6]
#L1=0; L2=R[no1][1]; B1=0; B2=R[no1][2]; #点->面のとき
skipL=1; skipB=1;
for j in range(L1,L2-l+1,skipL):
for k in range(B1,B2-b+1,skipB):
d_mode[i,no1,j,k]=Mode(\
"mode["+i+"]0_R[{0:03d}][{1:03d}_{2:03d}][{3:03d}_{4:03d}]"\
.format(no1,j,k,l,b))
for s in range(0,l):
for t in range(0,b):
d_mode[i,no1,j,k].addBreak(0,'inf')
d_mode[i,no1,j,k].addResource(res3PL[no1,j+s,k+t],1,"break")
d_mode[i,no1,j,k].addResource(res2S[no1],l*b,"break")
d_act[i].addModes(d_mode[i,no1,j,k])
prob.addTemporal(act[i],d_act[i],tempType="SS")
prob.addTemporal(d_act[i],act[i],tempType="SS")
for iw in [1,2,3,4]:
ii=ww[i,iw]
if ii!="0":
prob.addTemporal(d_act[i],act[ii],tempType="CC")
prob.addTemporal(act[ii],d_act[i],tempType="CC")
#----- 待機場所
d_act2={}
d_mode2={}
for i in wplace:
if data[i][1] in [1,2,3,4,5,6,7,8,9]:
data[i][7]=data[i][6]
d_act2[i]=prob.addActivity("空置_after_"+i)
for no in range(len(data[i][7])):
w=L1L2B1B2lb(R,data,i,7,no)
no1,L1,L2,B1,B2,l,b=w[0],w[1],w[2],w[3],w[4],w[5],w[6]
#L1=0; L2=R[no1][1]; B1=0; B2=R[no1][2];
skipL=1; skipB=1;
for j in range(L1,L2-l+1,skipL):
for k in range(B1,B2-b+1,skipB):
d_mode2[i,no1,j,k]=Mode(\
"mode["+i+"]1_R[{0:03d}][{1:03d}_{2:03d}][{3:03d}_{4:03d}]"\
.format(no1,j,k,l,b))
for s in range(0,l):
for t in range(0,b):
d_mode2[i,no1,j,k].addBreak(0,0) #'inf')
d_mode2[i,no1,j,k].addResource(res3PL[no1,j+s,k+t],0,"break")
d_mode2[i,no1,j,k].addResource(res2S[no1],0,"break")
d_act2[i].addModes(d_mode2[i,no1,j,k])
prob.addTemporal(d_act[i],d_act2[i],tempType="CS")
prob.addTemporal(d_act2[i],d_act[i],tempType="SC")
ii=data[ww[i,1]][4][0]
prob.addTemporal(act[ii],d_act2[i],tempType="SC")
prob.addTemporal(d_act2[i],act[ii],tempType="CS")
#=======================================================================
#[3.5]問題求解 step1
#=======================================================================
A=[]
for a in prob.act: A.append(a.name)
#print("アクティビティ:",A)
N=len(prob.act)
print("アクティビティ総数(含待機数):",N)
M=[]
for a in prob.act: M.append(len(a.modes))
#print("モード数:",M)
print("平均モード数:",round(sum(M)/N))
P=math.ceil(math.log10(round(sum(M)/N)**N))
print("問題の規模: 10**",P)
#-----
#prob.Params.Makespan=Ture
#prob.Params.Initial=False
#prob.Params.OutputFlag=False
#prob.Params.Neighborhood=20
#prob.Params.RandomSeed=1
prob.Params.TimeLimit=300 #50 or 300
prob.optimize()
filename="rcpsp63_step1.csv"
#print("writing "+filename)
prob.writeExcel(filename)
#-----------------------------------------------------------------------
#[3.6]計画上の調整期間における場所取り
#-----------------------------------------------------------------------
print(" ")
print("計画上の調整期間における場所取り")
jdata=[]; ldata=[]; mdata=[]; ndata=[]
data1={}
for i in data:
data1[i]=data[i].copy()
for a in prob.act:
if len(a.modes)==1: mode_nam=a.selected.name
else: mode_nam=a.selected
#print("__"+a.name,len(a.modes),mode_nam,a.start,a.completion)
if "場所_for_" in a.name:
i=a.name[7:] #運搬作業(期間1)
j=i[0:11]+"1"
ldata.append(j)
data1[j][3]=a.start
data1[j][2]=a.completion-a.start
r=int(mode_nam[16+6:19+6])
x=int(mode_nam[21+6:24+6])
y=int(mode_nam[25+6:28+6])
l=int(mode_nam[30+6:33+6])
b=int(mode_nam[34+6:37+6])
data1[j][6]=[[r,x,x+l,y,y+b]]
data1[j][8]=[l,b,0]
elif "空置_after_" in a.name:
i=a.name[9:]
#j=i[0:11]+"W"
mdata.append(i)
if a.completion-a.start>0:
data1[i][3]=a.start
data1[i][2]=a.completion-a.start
jdata.append(i)
#print(len(jdata),i,r,l,b)
if r in [1,2]: data1[i][7]=[R01,R02,R03,P03]
#elif r in [5,6]: data[i][7]=[R05,P07]
else: data1[i][7]=Q001+Q002+R00
elif "S01_" in a.name:
i=a.name[0:12]
ndata.append(i)
#if i[10:12]=="00": #運搬作業(期間1)
data1[i][3]=a.start
data1[i][2]=a.completion-a.start #不要
#data2[i][3]=a.start
#data2[i][2]=a.completion-a.start
print(len(ldata),len(mdata),len(ndata),len(jdata))
#sys.exit()
001
002
003
004
005
006
007
008
009
010
011
012
013
014
015
016
017
018
019
020
021
022
023
024
025
026
027
028
029
030
031
032
033
034
035
036
037
# reading data ... done: 1.03(s)
# random seed: 1
# tabu tenure: 1
# cpu time limit: 300.00(s)
# iteration limit: 1073741823
# computing all-pairs longest paths and strongly connected components ... done
#scc 88
objective value = 1000000510 (cpu time = 0.13(s), iteration = 0)
0: 0.14(s): 1000000510/1000000510
objective value = 1000000493 (cpu time = 1.16(s), iteration = 8)
objective value = 1000000452 (cpu time = 1.30(s), iteration = 9)
objective value = 1000000378 (cpu time = 7.00(s), iteration = 66)
objective value = 1000000333 (cpu time = 7.13(s), iteration = 67)
objective value = 1000000241 (cpu time = 7.29(s), iteration = 69)
objective value = 1000000203 (cpu time = 7.81(s), iteration = 72)
objective value = 1000000125 (cpu time = 8.63(s), iteration = 82)
objective value = 1000000091 (cpu time = 24.80(s), iteration = 215)
objective value = 1000000057 (cpu time = 58.61(s), iteration = 484)
objective value = 1000000027 (cpu time = 58.79(s), iteration = 485)
objective value = 47926 (cpu time = 58.86(s), iteration = 486)
objective value = 47532 (cpu time = 59.30(s), iteration = 487)
objective value = 47494 (cpu time = 62.24(s), iteration = 491)
objective value = 47467 (cpu time = 64.17(s), iteration = 493)
objective value = 47438 (cpu time = 65.10(s), iteration = 494)
objective value = 47382 (cpu time = 66.72(s), iteration = 495)
objective value = 47282 (cpu time = 68.29(s), iteration = 497)
objective value = 47123 (cpu time = 72.08(s), iteration = 500)
objective value = 47052 (cpu time = 75.10(s), iteration = 503)
objective value = 47020 (cpu time = 133.25(s), iteration = 563)
objective value = 47017 (cpu time = 134.67(s), iteration = 564)
objective value = 47016 (cpu time = 135.79(s), iteration = 565)
objective value = 46995 (cpu time = 150.45(s), iteration = 581)
objective value = 46988 (cpu time = 154.02(s), iteration = 584)
objective value = 46968 (cpu time = 156.10(s), iteration = 586)
objective value = 46942 (cpu time = 183.52(s), iteration = 618)
objective value = 46939 (cpu time = 185.59(s), iteration = 620)
objective value = 46893 (cpu time = 186.83(s), iteration = 622)
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
#=======================================================================
#iwhich=4 3プル型同時計画Step2: 待機の場所取りは面全体
if iwhich==4: #rcpsp71_4.csv
#=======================================================================
prob2=Model()
#-----------------------------------------------------------------------
#[4.0]リソースの定義(場所)
#-----------------------------------------------------------------------
#-----未使用のリソース
for id in R:
for i in range(0,R[id][1]):
for j in range(0,R[id][2]):
res3PL[id,i,j] =prob2.addResource(R[id][0]+"[{0:02d}_{1:02d}]".format(i,j),\
capacity=res3PL[id,i,j].residual)
#-----------------------------------------------------------------------
#[4.1]作業の定義
#-----------------------------------------------------------------------
act2={}
for i in jdata:
act2[i]=prob2.addActivity("待機_after_"+data[i][0][0:12])
#-----------------------------------------------------------------------
#[4.2]先行制約
#-----------------------------------------------------------------------
#-----日程固定
for i in jdata:
prob2.addTemporal("source",act2[i],tempType="SS",delay= data1[i][3])
prob2.addTemporal(act2[i],"source",tempType="SS",delay=-data1[i][3])
#-----------------------------------------------------------------------
#[4.4]資源制約(作業場所)
#-----------------------------------------------------------------------
mode2={}
for i in jdata:
#print(i,data1[i][0])
for no in range(len(data1[i][7])):
#w=L1L2B1B2lb(R,data,i,7,no)
#no1,L1,L2,B1,B2,l,b=w[0],w[1],w[2],w[3],w[4],w[5],w[6]
#L1=0; L2=R[no1][1]; B1=0; B2=R[no1][2];
no1=data1[i][7][no][0];
L=R[no1][1]; B=R[no1][2];
L1=data1[i][7][no][1]; L2=data1[i][7][no][2];
B1=data1[i][7][no][3]; B2=data1[i][7][no][4];
l=math.floor(data1[i][8][0]); b=math.floor(data1[i][8][1]);
skipL=1; skipB=1;
for j in range(L1,L2-l+1,skipL):
for k in range(B1,B2-b+1,skipB):
mode2[i,no1,j,k]=Mode(\
"mode["+i+"]2_R[{0:03d}][{1:03d}_{2:03d}][{3:03d}_{4:03d}]"\
.format(no1,j,k,l,b),duration=data1[i][2])
for s in range(0,l):
for t in range(0,b):
mode2[i,no1,j,k].addResource(res3PL[no1,j+s,k+t],1)
#mode2[i,no1,j,k].addResource(res2S[no1,j,k],l*b)
act2[i].addModes(mode2[i,no1,j,k])
#-----------------------------------------------------------------------
#[4.5]問題求解
#-----------------------------------------------------------------------
A=[]
for a in prob2.act: A.append(a.name)
#print("アクティビティ:",A)
N=len(prob2.act)
print("アクティビティ総数(含待機数):",N)
M=[]
for a in prob2.act: M.append(len(a.modes))
#print("モード数:",M)
print("平均モード数:",round(sum(M)/N))
P=math.ceil(math.log10(round(sum(M)/N)**N))
print("問題の規模: 10**",P)
#-----
#prob2.Params.Makespan=True
#prob2.Params.Initial=False
#prob2.Params.OutputFlag=False
#prob2.Params.RandomSeed=1
prob2.Params.TimeLimit=300
prob2.optimize()
filename="rcpsp63_step2.csv"
#print("writing "+filename)
prob2.writeExcel(filename)
#sys.exit()
#=======================================================================
#eof
001
002
003
004
005
006
007
008
009
010
011
012
013
014
015
016
017
018
019
020
021
022
023
024
025
026
027
028
029
030
031
032
033
034
035
036
037
038
039
040
# reading data ... done: 88.61(s)
# random seed: 1
# tabu tenure: 1
# cpu time limit: 300.00(s)
# iteration limit: 1073741823
# computing all-pairs longest paths and strongly connected components ... done
#scc 41
objective value = 1000000038 (cpu time = 0.04(s), iteration = 0)
0: 0.04(s): 1000000038/1000000038
objective value = 1000000037 (cpu time = 0.05(s), iteration = 1)
objective value = 1000000036 (cpu time = 0.06(s), iteration = 2)
objective value = 1000000035 (cpu time = 0.08(s), iteration = 3)
objective value = 1000000034 (cpu time = 0.11(s), iteration = 4)
objective value = 1000000033 (cpu time = 0.12(s), iteration = 5)
objective value = 1000000032 (cpu time = 0.15(s), iteration = 6)
objective value = 1000000031 (cpu time = 0.17(s), iteration = 7)
objective value = 1000000029 (cpu time = 0.20(s), iteration = 8)
objective value = 1000000028 (cpu time = 0.22(s), iteration = 9)
objective value = 1000000027 (cpu time = 0.31(s), iteration = 11)
objective value = 1000000026 (cpu time = 0.36(s), iteration = 12)
objective value = 1000000025 (cpu time = 0.38(s), iteration = 13)
objective value = 1000000024 (cpu time = 0.60(s), iteration = 16)
objective value = 1000000022 (cpu time = 4.31(s), iteration = 17)
objective value = 1000000021 (cpu time = 4.34(s), iteration = 18)
objective value = 1000000020 (cpu time = 4.38(s), iteration = 19)
objective value = 1000000019 (cpu time = 4.40(s), iteration = 20)
objective value = 1000000018 (cpu time = 4.60(s), iteration = 23)
objective value = 1000000017 (cpu time = 5.85(s), iteration = 25)
objective value = 1000000016 (cpu time = 9.38(s), iteration = 26)
objective value = 1000000014 (cpu time = 9.42(s), iteration = 27)
objective value = 1000000013 (cpu time = 9.46(s), iteration = 28)
objective value = 1000000010 (cpu time = 9.59(s), iteration = 30)
objective value = 1000000008 (cpu time = 18.79(s), iteration = 71)
objective value = 1000000007 (cpu time = 18.86(s), iteration = 72)
objective value = 1000000006 (cpu time = 19.34(s), iteration = 75)
objective value = 1000000005 (cpu time = 20.77(s), iteration = 77)
objective value = 1000000004 (cpu time = 29.02(s), iteration = 80)
objective value = 1000000003 (cpu time = 53.04(s), iteration = 92)
objective value = 1000000002 (cpu time = 53.12(s), iteration = 93)
objective value = 0 (cpu time = 53.24(s), iteration = 94)
159
160
161
162
163
164
165
166
167
168
#rcpsp64.py プル型同時計画(面)
:
#----- 作業場所
d_act={}
d_mode={}
for i in idata:
if data[i][1] in [1,2,3,4,5,6,7,8,9] and data[i][6]!=0:
d_act[i]=prob.addActivity("場所_for_"+i)
for no in range(len(data[i][6])):
w=L1L2B1B2lb(R,data,i,6,no)
no1,L1,L2,B1,B2,l,b=w[0],w[1],w[2],w[3],w[4],w[5],w[6]
L1=0; L2=R[no1][1]; B1=0; B2=R[no1][2]; #点->面のとき
: