Walcott-Zak’s observer…Homework
[1] 制御対象の状態空間表現として次式を考えます。
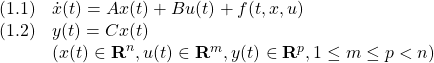
ただし、![]() はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
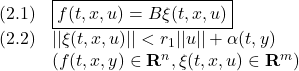
●このとき、Walcott-Zakは次のSMオブザーバを提案しています(![]() )。
)。
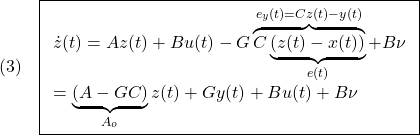
ここで、![]() は
は![]() が安定行列となるように選ばれているとします。また、
が安定行列となるように選ばれているとします。また、
![]()
を満足する![]() と、ある
と、ある![]() に対して
に対して
![]()
が満足されているものとします。このとき、![]() は
は
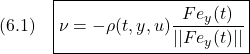
ただし
![]()
のように与えます。
これは、通常のオブザーバと同様に、出力の推定誤差 ![]() をフィードバックした上で、出力の推定誤差のスイッチング動作が加えられています。これにより、モデル誤差、非線形要素、外乱などの影響があるにも拘わらず、
をフィードバックした上で、出力の推定誤差のスイッチング動作が加えられています。これにより、モデル誤差、非線形要素、外乱などの影響があるにも拘わらず、![]() の超平面に載せることが考えられます。
の超平面に載せることが考えられます。
[2] (3)から(1.1)を辺々引き算して、誤差方程式
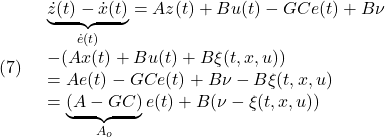
すなわち
![]()
を得ます。このとき、リャプノフ関数
![]()
に対して
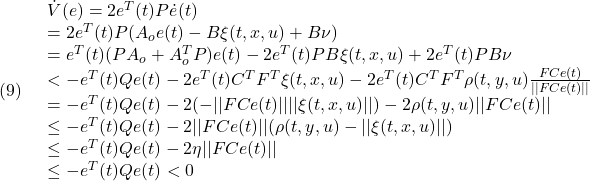
を得て、2次安定性が成り立ちます。したがって、ある有限時間で、次の超平面上でのスライディングモードが達成されます。
![]()
[3] 適当な座標変換を用いて、(1.1)の状態空間表現として次式が得られます。
![Rendered by QuickLaTeX.com \displaystyle{(11.1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} {\bar A}_{11} & {\bar A}_{12} \\ {\bar A}_{21} & {\bar A}_{22} \\ \end{array}\right] }_{{\bar A}=TAT^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} + \boxed{\underbrace{ \left[\begin{array}{c} 0_{n-p\times p}\\ {\bar B}_{2} \end{array}\right] }_{{\bar B}=TB}} (u(t)+\xi(t))\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-df89f2c8c5027f65f3d1b001df56a333_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11.2)\quad y(t) = \boxed{\underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] }_{{\bar C}=CT^{-1}}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d15eb88c68556f6e054c3e64d14d9b4a_l3.png)
ただし、![]() は安定行列です。
は安定行列です。
●これは予備的検討における(3.1)と(3.2)と同じタイプですから、そこでの(18)に相当する
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \dot{\hat x}(t)=A\hat{x}(t)+Bu(t)-G_\ell Ce(t)+G_n\nu\\ G_\ell=T_o^{-1}\left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right]\\ G_n=||{\cal D}_{2}||T_o^{-1}\left[\begin{array}{c} 0_{n-p\times p}\\ I_p \end{array}\right]\\ \displaystyle{\nu=-\rho(t,y,u)\frac{P_2e_y(t)}{||P_2e_y(t)||} \quad(P_2{\cal A}_{22}^{s}+{\cal A}_{22}^{s}^TP_2<0)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4b315d5f9deb1d92118c05143cc36e33_l3.png)
を設計できます。これから、(3)と(6.1)における![]() と
と![]() を、次のように定めることが提案されています。
を、次のように定めることが提案されています。
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \boxed{G=(T_LT_bT_c)^{-1}\left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-99565ec8e7483b355f59c24131882a38_l3.png)
![]()
ここまでの手順を、関数smobs2としてプログラムすることにします。
Note C-83: (11)への座標変換
いま
![]()
と分割し、座標変換行列
![]()
を定義します。このとき
![]()
を得ます、また
![]()
と表すと、![]() に注意して
に注意して
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \bar{B}=TB= \left[\begin{array}{cc} I_{n-p} & {P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right] \left[\begin{array}{cc} {\tilde P}_{11} & {\tilde P}_{12} \\ {\tilde P}_{21} & {\tilde P}_{22} \end{array}\right] \left[\begin{array}{cc} 0 \\ I_p \end{array}\right] F^T\\ =\left[\begin{array}{cc} {\tilde P}_{12} + {P}_{11}^{-1}{P}_{12}{\tilde P}_{22} \\ {\tilde P}_{22} \end{array}\right] F^T= \underbrace{\left[\begin{array}{cc} 0 \\ {\tilde P}_{22}F^T \end{array}\right] }_{\left[\begin{array}{cc} 0 \\ {\bar B}_{2} \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ecf550e6e68e139dfd9b70a2c51821a0_l3.png)
および
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} \bar{P}=T^{-T}PT^{-1}\\ = \left[\begin{array}{cc} I_{n-p} & 0 \\ -{P}_{12}^T{P}_{11}^{-1} & I_p \end{array}\right] \left[\begin{array}{cc} {P}_{11} & {P}_{12} \\ {P}_{21} & {P}_{22} \end{array}\right] \left[\begin{array}{cc} I_{n-p} & -{P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right]\\ = \left[\begin{array}{cc} {P}_{11} & {P}_{12} \\ 0 & {P}_{22}-{P}_{12}^T{P}_{11}^{-1}{P}_{12} \end{array}\right] \left[\begin{array}{cc} I_{n-p} & -{P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right]\\ =\underbrace{\left[\begin{array}{cc} {P}_{11} & 0 \\ 0 & {P}_{22}-{P}_{21}{P}_{11}^{-1}{P}_{12} \end{array}\right] }_{\left[\begin{array}{cc} {\bar P}_{1} & 0 \\ 0 & {\bar P}_{2} \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d939c6b48cf57392a69499adfa73c15a_l3.png)
を得ます。また
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \bar{A}=TAT^{-1}\\ = \left[\begin{array}{cc} I_{n-p} & {P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right] \left[\begin{array}{cc} {A}_{11} & {A}_{12} \\ {A}_{21} & {A}_{22} \end{array}\right] \left[\begin{array}{cc} I_{n-p} & -{P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right]\\ = \left[\begin{array}{cc} {A}_{11}+{P}_{11}^{-1}{P}_{12}{A}_{21} & {A}_{12}+ {P}_{11}^{-1}{P}_{12}{A}_{22}\\ {A}_{21} & {A}_{22} \end{array}\right] \left[\begin{array}{cc} I_{n-p} & -{P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right]\\ =\underbrace{\left[\begin{array}{cc} {A}_{11}+{P}_{11}^{-1}{P}_{12}{A}_{21} & * \\ {A}_{21} & {A}_{22}-{A}_{21}{P}_{11}^{-1}{P}_{12} \end{array}\right] }_{\left[\begin{array}{cc} {\bar A}_{11} & {\bar A}_{12} \\ {\bar A}_{21} & {\bar A}_{22} \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-818dd08ad7b025fcdf6ac9148b5e312b_l3.png)
より
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \bar{A}_o=\underbrace{TA_oT^{-1} }_{\left[\begin{array}{cc} {\bar A}_{o11} & {\bar A}_{o12} \\ {\bar A}_{o21} & {\bar A}_{o22} \end{array}\right]} =T(A-GC)T^{-1}\\ =\underbrace{TAT^{-1}}_{ \left[\begin{array}{cc} {\bar A}_{11} & {\bar A}_{12} \\ {\bar A}_{21} & {\bar A}_{22} \end{array}\right]} -\underbrace{TGCT^{-1}} _{\left[\begin{array}{cc} 0 & TG \end{array}\right]} = \left[\begin{array}{cc} {\bar A}_{11} & * \\ {\bar A}_{21} & * \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ac09c08dae61878b5898912612961935_l3.png)
すなわち![]() であることに注意します。
であることに注意します。
●本文(4)の左右から、![]() と
と![]() をかけて
をかけて
![]()
また本文(5)の左から、![]() をかけて
をかけて
![]()
を得ます。したがって、座標変換後も、本文(4)と(5)は同様に成り立ちます。
(9)において(6)と(8)を考慮すると
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \left[\begin{array}{cc} {\bar P}_{1} & 0 \\ 0 & {\bar P}_{2} \end{array}\right] \left[\begin{array}{cc} {\bar A}_{o11} & {\bar A}_{o12} \\ {\bar A}_{o21} & {\bar A}_{o22} \ \end{array}\right] +\left[\begin{array}{cc} {\bar A}_{o11} & {\bar A}_{o12} \\ {\bar A}_{o21} & {\bar A}_{o22} \ \end{array}\right]^T \left[\begin{array}{cc} {\bar P}_{1} & 0 \\ 0 & {\bar P}_{2} \end{array}\right]\\ =- \left[\begin{array}{cc} \bar{Q}_{11} & \bar{Q}_{12} \\ \bar{Q}_{12}^T & \bar{Q}_{22} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f9c197610a2dc08d37d7807a77250d9d_l3.png)
すなわち
![]()
したがって、![]() は安定行列となります。
は安定行列となります。
また(10)において(3)と(5)を考慮すると
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \underbrace{\left[\begin{array}{cc} 0 & I_p \end{array}\right]}_{\bar{C}^T}F^T=\underbrace{\left[\begin{array}{cc} {\bar P}_{1} & 0 \\ 0 & {\bar P}_{2} \end{array}\right]}_{\bar P}\underbrace{\left[\begin{array}{cc} 0 \\ {\bar B}_{2} \end{array}\right]}_{\bar B} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-25481cf05987d97cf1d660f8462287a3_l3.png)
すなわち
![]()