[1] 制御対象の状態空間表現として次式を考えます。
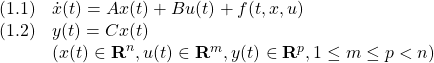
ただし、![]() はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
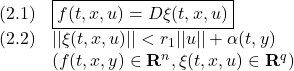
●適当な座標変換![]() によって次式が得られていると仮定します。
によって次式が得られていると仮定します。
![Rendered by QuickLaTeX.com \displaystyle{(3.1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} {\cal A}_{11} & {\cal A}_{12} \\ {\cal A}_{21} & {\cal A}_{22} \\ \end{array}\right] }_{T_oAT_o^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} + \underbrace{ \left[\begin{array}{c} {\cal B}_{1}\\ {\cal B}_{2} \end{array}\right] }_{T_oB} u(t) +\boxed{ \underbrace{ \left[\begin{array}{c} 0_{n-p\times p}\\ {\cal D}_{2} \end{array}\right] }_{T_oD}} \xi(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c84baa48a735c227a2adb1d7a835b4a4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3.2)\quad y(t) = \boxed{\underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] }_{CT_o^{-1}}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-90635122c9b9569be2466b719f5f1954_l3.png)
ただし、![]() は安定行列であることを仮定します。
は安定行列であることを仮定します。
●このとき次のSMオブザーバを考えます。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \boxed{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\hat x}_1(t)\\ \dot{\hat y}(t) \end{array}\right] }_{\dot{\hat x}'(t)} = \underbrace{ \left[\begin{array}{cc} {\cal A}_{11} & {\cal A}_{12} \\ {\cal A}_{21} & {\cal A}_{22} \\ \end{array}\right] }_{T_oAT_o^{-1}} \underbrace{ \left[\begin{array}{c} \hat{x}_1(t)\\ \hat{y}(t) \end{array}\right] }_{\hat{x}'(t)} + \underbrace{ \left[\begin{array}{c} {\cal B}_{1}\\ {\cal B}_{2} \end{array}\right] }_{T_oB} u(t)\\ - \left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right] \underbrace{(\hat{y}(t)-y(t))}_{e_y(t)} + \left[\begin{array}{c} 0_{n-p\times p}\\ I_p \end{array}\right] \nu \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-66e4a486014204d000a249eb1c1c592b_l3.png)
ここで、![]() は安定行列として選ばれているとします。また、
は安定行列として選ばれているとします。また、
![]()
を満足する![]() を用いて、
を用いて、![]() は
は
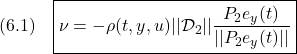
ただし
![]()
のように与えます。
以下では、モデル誤差、非線形要素、外乱などの影響があるにも拘わらず、状態オブザーバを構成できるを検討します。
[2] (4)から(3.1)を辺々引き算して、次の誤差方程式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \left[\begin{array}{c} \dot{\hat x}_1(t)-\dot{x}_1(t)\\ \dot{\hat y}(t)-\dot{y}(t) \end{array}\right] = \left[\begin{array}{cc} {\cal A}_{11} & {\cal A}_{12} \\ {\cal A}_{21} & {\cal A}_{22} \\ \end{array}\right] \left[\begin{array}{c} \hat{x}_1(t)-x_1(t)\\ \hat{y}(t)-y(t) \end{array}\right]\\ - \left[\begin{array}{cc} 0 & {\cal A}_{12}\\ 0 & {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right] \left[\begin{array}{c} \hat{x}_1(t)-x_1(t)\\ \hat{y}(t)-y(t) \end{array}\right] + \left[\begin{array}{c} 0_{n-p}\\ \nu-{\cal D}_{2}\xi(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c17498fb75a8ddddcfaced948ff16ca_l3.png)
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(7')\quad \boxed{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\hat x}_1(t)-\dot{x}_1(t)\\ \dot{\hat y}(t)-\dot{y}(t) \end{array}\right] }_{\left[\begin{array}{c} \dot{e}_1(t)\\ \dot{e}_y(t) \end{array}\right]} = \left[\begin{array}{cc} {\cal A}_{11} & 0_{n-p\times p} \\ {\cal A}_{21} & {\cal A}_{22}^{s} \\ \end{array}\right] \underbrace{ \left[\begin{array}{c} \hat{x}_1(t)-x_1(t)\\ \hat{y}(t)-y(t) \end{array}\right] }_{\left[\begin{array}{c} {e}_1(t)\\ {e}_y(t) \end{array}\right]}\\ + \left[\begin{array}{c} 0_{n-p}\\ \nu-{\cal D}_{2}\xi(t) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eca857318ee4a936235a33d8531cf6bf_l3.png)
●この誤差システムの2次安定性を示します。(5)の解![]() を用いて
を用いて
![]()
を定義し、
![]()
の解![]() を用いて、リャプノフ関数
を用いて、リャプノフ関数
![]()
を考えます。このとき
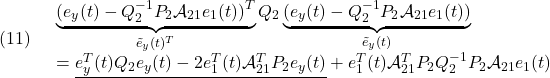
および
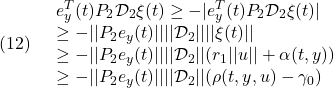
に注意して
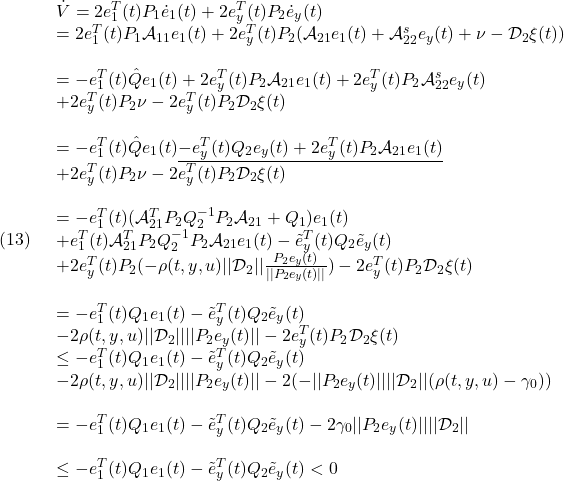
●一方、誤差の振舞いはある有限時間で次の超平面上でのスライディングモードとなることがわかります。
![]()
実際、(10)の第2項
![]()
に対して、(12)に注意して
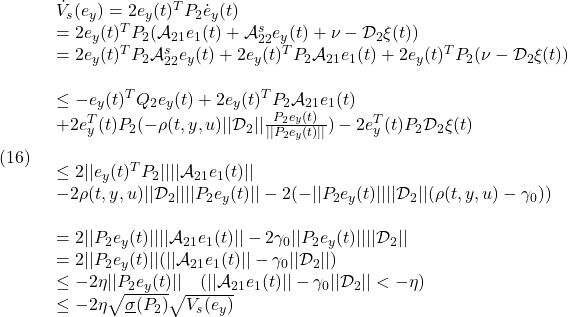
ただし
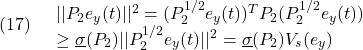
●SMオブザーバ(4)と(6.1)を再掲すると
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\hat x}_1(t)\\ \dot{\hat y}(t) \end{array}\right] }_{\dot{\hat x}'(t)} = \underbrace{ \left[\begin{array}{cc} {\cal A}_{11} & {\cal A}_{12} \\ {\cal A}_{21} & {\cal A}_{22} \\ \end{array}\right] }_{T_oAT_o^{-1}} \underbrace{ \left[\begin{array}{c} \hat{x}_1(t)\\ \hat{y}(t) \end{array}\right] }_{\hat{x}'(t)} + \underbrace{ \left[\begin{array}{c} {\cal B}_{1}\\ {\cal B}_{2} \end{array}\right] }_{T_oB} u(t)\\ - \left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right] \underbrace{(\hat{y}(t)-y(t))}_{e_y(t)} + \left[\begin{array}{c} 0_{n-p\times p}\\ I_p \end{array}\right] \nu \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-47ff921fcda56486a051274cf1f22315_l3.png)
![]()
これは、![]() より
より![]() としてよいので、次のように表すことができます。
としてよいので、次のように表すことができます。
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \boxed{\begin{array}{l} \dot{\hat x}(t)=A\hat{x}(t)+Bu(t)-G_\ell e_y(t)+G_n\nu\\ G_\ell=T_o^{-1}\left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right]\\ G_n=||{\cal D}_{2}||T_o^{-1}\left[\begin{array}{c} 0_{n-p\times p}\\ I_p \end{array}\right]\\ \displaystyle{\nu=-\rho(t,y,u)\frac{P_2e_y(t)}{||P_2e_y(t)||} \quad(P_2{\cal A}_{22}^{s}+{\cal A}_{22}^{s}^TP_2<0)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7107375b58980fcf0a852de479bd7ce3_l3.png)
[2] 以上の議論は(3.1)と(3.2)の形式を得るための座標変換行列![]() の存在が前提になります。これについて調べるために、出力FB型SM制御(p>m)で得られていた次の結果に注目します。
の存在が前提になります。これについて調べるために、出力FB型SM制御(p>m)で得られていた次の結果に注目します。
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{ll} (18.1*)&(T_aT_bT_c)A(T_aT_bT_c)^{-1}= \left[\begin{array}{cccc} A_{11}^o & A_{12}^o & A_{121}^m & A_{121}\\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221}\\ 0_{p-m\times r} & A_{21}^o & A_{22}^m & A_{1222}\\ A_{2120} & A_{2121} & A_{2122} & A_{22} \end{array}\right]\\ &(A_{11}^o\in{\rm\bf R}^{r\times r},A_{22}^o\in{\rm\bf R}^{n-p-r\times n-p-r},A_{22}^m\in{\rm\bf R}^{p-m\times p-m},A_{22}\in{\rm\bf R}^{m\times m})\\ (18.2*)&(T_aT_bT_c)B= \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\ B_2 \end{array}\right]\\ (18.3*)&C(T_aT_bT_c)^{-1}= \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-24aba4138d204a391e18f69edcd60c03_l3.png)
ここで、![]() は可観測対、
は可観測対、![]() の固有値は
の固有値は![]() の不変零点でした。この不変零点は安定であること、
の不変零点でした。この不変零点は安定であること、![]() が仮定されていました。
が仮定されていました。
●これは![]() の場合ですが、
の場合ですが、![]() の場合も、
の場合も、![]() として同様にして次式を得ます。
として同様にして次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{ll} (19.1)&(T_aT_bT_c)A(T_aT_bT_c)^{-1}= \underbrace{ \left[\begin{array}{cc|cc} A_{11}^o & A_{12}^o & A_{121}^m & A_{121}\\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221}\\\hline 0_{p-q\times r} & A_{21}^o & A_{22}^m & A_{1222}\\ A_{2120} & A_{2121} & A_{2122} & A_{22} \end{array}\right] }_{ \left[\begin{array}{c|c} A_{11} & *\\\hline A_{211} & *\\ * & * \end{array}\right] }\\ &(A_{11}\in{\rm\bf R}^{n-p\times n-p},A_{211}\in{\rm\bf R}^{p-q\times n-p})\\ (19.2)&(T_aT_bT_c)D= \left[\begin{array}{c} 0_{r\times q} \\ 0_{n-p-r\times q} \\ 0_{p-q\times q} \\ D_2 \end{array}\right]\\ (19.3)&C(T_aT_bT_c)^{-1}= \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0e35543abcf691542b05178054d4aac2_l3.png)
ここで、![]() は可観測対、
は可観測対、![]() の固有値は
の固有値は![]() の不変零点です。同様に、この不変零点は安定で、
の不変零点です。同様に、この不変零点は安定で、![]() を仮定します。
を仮定します。
●![]() を安定行列とする
を安定行列とする![]() を用いて、追加の座標変換行列を
を用いて、追加の座標変換行列を
![]()
とすると
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{ll} (21.1)&T_L(T_aT_bT_c)A(T_aT_bT_c)^{-1}= \underbrace{\left[\begin{array}{cc} I_{n-p} & \left[\begin{array}{cc} L & 0_{n-p\times q} \end{array}\right] \\ 0_{p\times n-p} & T \end{array}\right]}_{T_L} \left[\begin{array}{c|c} A_{11} & *\\\hline A_{211} & *\\ * & * \end{array}\right]T_L\\ &= \left[\begin{array}{c|c} A_{11}+LA_{211} & *\\\hline * & * \end{array}\right] \underbrace{\left[\begin{array}{cc} I_{n-p} & \left[\begin{array}{cc} L & 0_{n-p\times q} \end{array}\right] \\ 0_{p\times n-p} & T \end{array}\right]}_{T_L}\\ (21.2)&T_L(T_aT_bT_c)D= \underbrace{\left[\begin{array}{cc} I_{n-p} & \left[\begin{array}{cc} L & 0_{n-p\times q} \end{array}\right] \\ 0_{p\times n-p} & T \end{array}\right]}_{T_L} \left[\begin{array}{c} 0_{n-p\times q} \\ 0_{p-q\times q} \\ D_2 \end{array}\right]\\ (21.3)&C(T_aT_bT_c)^{-1}= \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] \underbrace{\left[\begin{array}{cc} I_{n-p} & \left[\begin{array}{cc} L & 0_{n-p\times q} \end{array}\right] \\ 0_{p\times n-p} & T \end{array}\right]}_{T_L} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-68fa24b51933a9c473610573a0e51069_l3.png)
すなわち
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{ll} (22.1)&(T_LT_aT_bT_c)A(T_LT_aT_bT_c)^{-1}= \left[\begin{array}{c|c} A_{11}+LA_{211} & *\\\hline * & * \end{array}\right]\\ (22.2)&(T_LT_aT_bT_c)D= \left[\begin{array}{c} 0_{n-p\times q} \\ T\left[\begin{array}{c} 0_{p-q\times q} \\ D_2 \end{array}\right] \end{array}\right]\\ (22.3)&C(T_LT_aT_bT_c)^{-1}= \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-92e44180ccc9fb5eea4f190d7391699c_l3.png)
を得ます。したがって、![]() は
は
![]()
と選べばよいことが分かります。
ここまでの手順を、関数ca_form2としてプログラムすることにします。
さらに、関数smobs1としてプログラムすることにします。