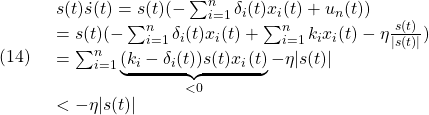問題設定…Homework
[1] 制御対象の状態方程式として次式を考えます。
![]()
ここで、![]() はモデル誤差、非線形要素、外乱などの影響を表し、有界かつ未知とします。これに対し、次のスイッチング関数を定義します。
はモデル誤差、非線形要素、外乱などの影響を表し、有界かつ未知とします。これに対し、次のスイッチング関数を定義します。
![]()
以下では、(1)の解が、ある時刻![]() に対して
に対して
![]()
を満足するような状況、すなわちスライディングモードを考えます。
以上の準備の下で、スライディングモード制御問題は次のように記述されます。
|
問題1: 動的システムの振舞いを閉じ込める超平面 問題2: 有限時刻 |
この問題の解、SMC則は、次のように表されます。
![]()
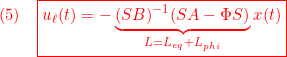
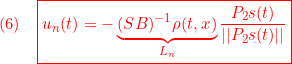
ここで、![]() は正則行列であることを仮定しています。また設計パラメータは、安定行列
は正則行列であることを仮定しています。また設計パラメータは、安定行列![]() 、スカラー
、スカラー![]() です。
です。![]() は次式から定まる正定行列です。
は次式から定まる正定行列です。
![]()
以下ではこの解の妥当性を2次安定化の観点から検討します。
[2] いま(1)において![]() 、すなわち
、すなわち
![]()
とし、![]() の正則性を仮定します。
の正則性を仮定します。![]() において、スライディングモード時の制御則は等価制御と呼ばれ、次式のように求められます。
において、スライディングモード時の制御則は等価制御と呼ばれ、次式のように求められます。
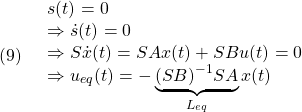
これによる閉ループ系は次式となります。
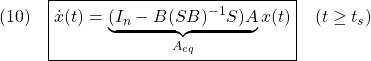
ちなみに、(4)の第1項![]() は、この等価制御をベースして
は、この等価制御をベースして
![]()
のように構成されています。この![]() の役割についてはあとで述べます。
の役割についてはあとで述べます。
[3] いま(1)において![]() の場合、適合サイズをもつ行列
の場合、適合サイズをもつ行列![]() を用いて
を用いて
![]()
のように表されると仮定します。このとき、等価制御は
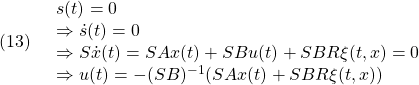
となります。これによる閉ループ系は次式となります。
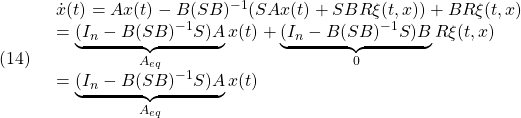
すなわちマッチング条件とよばれる(12)が成り立つとき、スライディングモード時は![]() の影響を受けないことが分かります。
の影響を受けないことが分かります。
演習…Flipped Classroom
![]() 次の剛体振子の状態方程式
次の剛体振子の状態方程式
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} 0 & 1\\ 0 & 0 \end{array}\right] }_{A} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]+ \underbrace{ \left[\begin{array}{c} 0\\ 1 \end{array}\right] }_{B} u(t)+ \underbrace{ \left[\begin{array}{c} 0\\ -a\sin x_1(t) \end{array}\right] }_{f} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5f207f5d4fc2ee68a8e5cbb3983a83af_l3.png)
に対して、スイッチング関数を
![Rendered by QuickLaTeX.com \displaystyle{ s(t)= \underbrace{ \left[\begin{array}{cc} m & 1 \end{array}\right] }_{S} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3a1328c53082e4bc421dbdb031541ce8_l3.png)
と選ぶとき、SMC則の線形制御の部分は次式となることを示せ。
![]()
※![]() を改めて
を改めて![]() とおけば、可到達条件のところで述べた次式(14)となります。
とおけば、可到達条件のところで述べた次式(14)となります。
![]()
![]() 上の剛体振子の状態方程式についてマッチング条件(12)を調べよ。
上の剛体振子の状態方程式についてマッチング条件(12)を調べよ。
Note C211入力系の場合
●ここでは次の1入力系を考えます。
![]()
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad A= \left[\begin{array}{cccc|c} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & 0 & \vdots \\ \vdots & & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & 0 & 1 \\\hline -a_1 & -a_2 & \cdots & \cdots & -a_n \end{array}\right],\quad B=\left[\begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \\\hline 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ef11f7c43ce31771dd5871c77048689e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{r} \Delta A(t)= \left[\begin{array}{cccc|c} 0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & 0 & \vdots \\ \vdots & & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & 0 & 0 \\\hline -\delta_1(t) & -\delta_2(t) & \cdots & \cdots & -\delta_n(t) \end{array}\right]\\ k_i^-\le\delta_i(t)\le k_i^+\quad(i=1,\cdots,n) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-34525207b48d6d25b7f649dbf4d8bc0a_l3.png)
また次のスイッチング関数を考えます。
![]()
![]()
このとき、SMC則
![]()
を可到達条件を満たすように構成することを考えます。
●線形制御![]() は、
は、
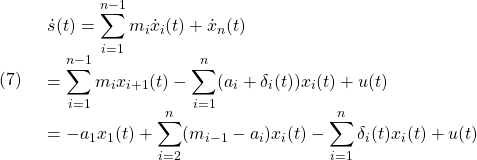
において、![]() とおいて
とおいて
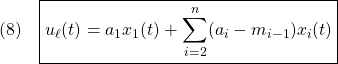
のように定めます。
●![]() の候補として次の2つを考えます。
の候補として次の2つを考えます。
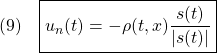
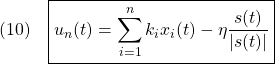
以下では、これらが適当な条件の下で可到達条件![]() を満足しSMC則になることを示します。
を満足しSMC則になることを示します。
(9)の場合:
![]()
を満足する![]() を選ぶと
を選ぶと
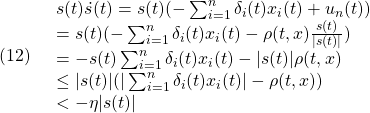
(10)の場合:
![]()
のように![]() を選ぶと
を選ぶと