Utkin’s Observer…Homework
[1] 次の制御対象のモデルを考えます。
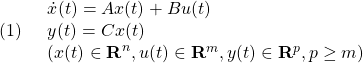
ただし、![]() は列フルランク、
は列フルランク、![]() は行フルランクをもち、
は行フルランクをもち、![]() は可観測対とします。
は可観測対とします。
●行列![]() を
を![]() の形にするために、座標変換
の形にするために、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} = \underbrace{ \left[\begin{array}{cc} N_c^T \\ C \\ \end{array}\right] }_{T_c} x(t) \Leftrightarrow x(t)= \underbrace{ \left[\begin{array}{cc} N_c^T \\ C \\ \end{array}\right]^{-1} }_{T_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4db3d40a6624450f2c64ca791f380fe1_l3.png)
を行うと(![]() は
は![]() を正則とする適当な行列)、次式を得ます。
を正則とする適当な行列)、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(3.1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} A_{c11} & A_{c12} \\ A_{c21} & A_{c22} \\ \end{array}\right] }_{T_cAT_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} + \underbrace{ \left[\begin{array}{c} B_{c1}\\ B_{c2} \end{array}\right] }_{T_cB} u(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-644186c09de8b1938a61eb3a18489a90_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3.2)\quad y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] }_{CT_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-58c311e6be5fde3b8343f975d58b0d2a_l3.png)
[2] Utkinは次のオブザーバを提案しています。
![Rendered by QuickLaTeX.com \displaystyle{(4.1)\quad \boxed{\begin{array}{l} \left[\begin{array}{c} \dot{\hat x}_1(t)\\ \dot{\hat y}(t) \end{array}\right] = \left[\begin{array}{cc} A_{c11} & A_{c12} \\ A_{c21} & A_{c22} \\ \end{array}\right] \left[\begin{array}{c} \hat{x}_1(t)\\ \hat{y}(t) \end{array}\right] + \left[\begin{array}{c} B_{c1}\\ B_{c2} \end{array}\right] u(t)\\ + \left[\begin{array}{c} L\\ -I_p \end{array}\right] \nu \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-be4b4ad4f240be627b5ee9bf2dfec609_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4.2)\quad \boxed{\nu=M \left[\begin{array}{c} {\rm sgn}(\hat{y}_1(t)-y_1(t))\\ \vdots\\ {\rm sgn}(\hat{y}_p(t)-y_p(t)) \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e7bc0ad75dd6f59af1617db5c3d71ce3_l3.png)
ここで、![]() と
と![]() は設計パラメータです。
は設計パラメータです。
通常のオブザーバは、出力の推定誤差 ![]() をフィードバックしますが、上のオブザーバは出力の推定誤差のスイッチング動作が加えられています。これにより、
をフィードバックしますが、上のオブザーバは出力の推定誤差のスイッチング動作が加えられています。これにより、![]() の超平面に載せることが考えられます。
の超平面に載せることが考えられます。
●(4.1)から(3.1)を辺々引き算して
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \underbrace{ \left[\begin{array}{c} \dot{\hat x}_1(t)-\dot{x}_1(t)\\ \dot{\hat y}(t)-\dot{y}(t) \end{array}\right] }_{\left[\begin{array}{c} \dot{e}_1(t)\\ \dot{e}_y(t) \end{array}\right]} = \left[\begin{array}{cc} A_{c11} & A_{c12} \\ A_{c21} & A_{c22} \\ \end{array}\right] \underbrace{ \left[\begin{array}{c} \hat{x}_1(t)-{x}_1(t)\\ \hat{y}(t)-{y}(t) \end{array}\right] }_{\left[\begin{array}{c} {e}_1(t)\\ {e}_y(t) \end{array}\right]} + \left[\begin{array}{c} 0\\ -\nu \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8c8ad91d08e2ba443b44f99ab4a83031_l3.png)
ここで、座標変換
![]()
を行うと、次の誤差方程式を得ます
![Rendered by QuickLaTeX.com \displaystyle{(7.1)\quad \boxed{\left[\begin{array}{c} \dot{\tilde e}_1(t)\\ \dot{e}_y(t) \end{array}\right] = \left[\begin{array}{cc} \tilde{A}_{c11} & \tilde{A}_{c12} \\ \tilde{A}_{c21} & \tilde{A}_{c22} \\ \end{array}\right] \left[\begin{array}{c} \tilde{e}_1(t)\\ {e}_y(t) \end{array}\right] + \left[\begin{array}{c} 0\\ -I_p \end{array}\right]\nu} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3e4c6bfa8770bfcf9a5e2e1e89effae_l3.png)
ただし
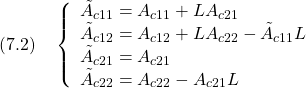
ここで、![]() が安定行列となるように
が安定行列となるように![]() が選ばれているとします。
が選ばれているとします。
●このとき、仮定
![]()
の下で、次の可到達条件が成り立ちます。
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{l} e^T_y(t)\dot{e}_y(t)=e^T_y(t)(\tilde{A}_{c21}\tilde{e}_1(t)+\tilde{A}_{c22}{e}_y(t)-\nu)\\\\ =e^T_y(t)\tilde{A}_{c21}\tilde{e}_1(t)+e^T_y(t)\tilde{A}_{c22}{e}_y(t)\\ -M \left[\begin{array}{c} \hat{y}_1(t)-y_1(t)\\ \vdots\\ \hat{y}_p(t)-y_p(t) \end{array}\right]^T \left[\begin{array}{c} {\rm sgn}(\hat{y}_1(t)-y_1(t))\\ \vdots\\ {\rm sgn}(\hat{y}_p(t)-y_p(t)) \end{array}\right]\\\\ =e^T_y(t)\tilde{A}_{c21}\tilde{e}_1(t)+e^T_y(t)\frac{1}{2}(\tilde{A}_{c22}+\tilde{A}^T_{c22}){e}_y(t)\\ -M(|\hat{y}_1(t)-y_1(t)|+\cdots+|\hat{y}_p(t)-y_p(t)|)\\\\ \le e^T_y(t)\tilde{A}_{c21}\tilde{e}_1(t)+\frac{1}{2}\bar\sigma(\tilde{A}_{c22}+\tilde{A}^T_{c22})e^T_y(t){e}_y(t)\\ -M(|\hat{y}_1(t)-y_1(t)|+\cdots+|\hat{y}_p(t)-y_p(t)|)\\\\ \le ||e_y(t)||(||\tilde{A}_{c21}\tilde{e}_1(t)||+\frac{1}{2}\bar\sigma(\tilde{A}_{c22}+\tilde{A}^T_{c22})||{e}_y(t)||)\\ -M(|\hat{y}_1(t)-y_1(t)|+\cdots+|\hat{y}_p(t)-y_p(t)|)\\\\ < ||e_y(t)||(M-\eta)-M(|\hat{y}_1(t)-y_1(t)|+\cdots+|\hat{y}_p(t)-y_p(t)|)\\ \le -\eta||e_y(t)||+M\underbrace{(||e_y(t)||-(|\hat{y}_1(t)-y_1(t)|+\cdots+|\hat{y}_p(t)-y_p(t)|))}_{\le0}\\ \le -\eta||e_y(t)||<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e20cc8c96c530a7504d6d40df37a524b_l3.png)
●これはSM標準形(7.1)に対してスイッチング関数を
![]()
と選ぶとき、スイッチング動作(4.2)によって![]() となることを示しています。このとき(7.1)から
となることを示しています。このとき(7.1)から
![]()
を得て、![]() も零の漸近するので、状態オブザーバ(4.1)が構成されていることが分かります。
も零の漸近するので、状態オブザーバ(4.1)が構成されていることが分かります。
[3] 以上の結果を数値例で確かめてみます。
| MATLAB |
|
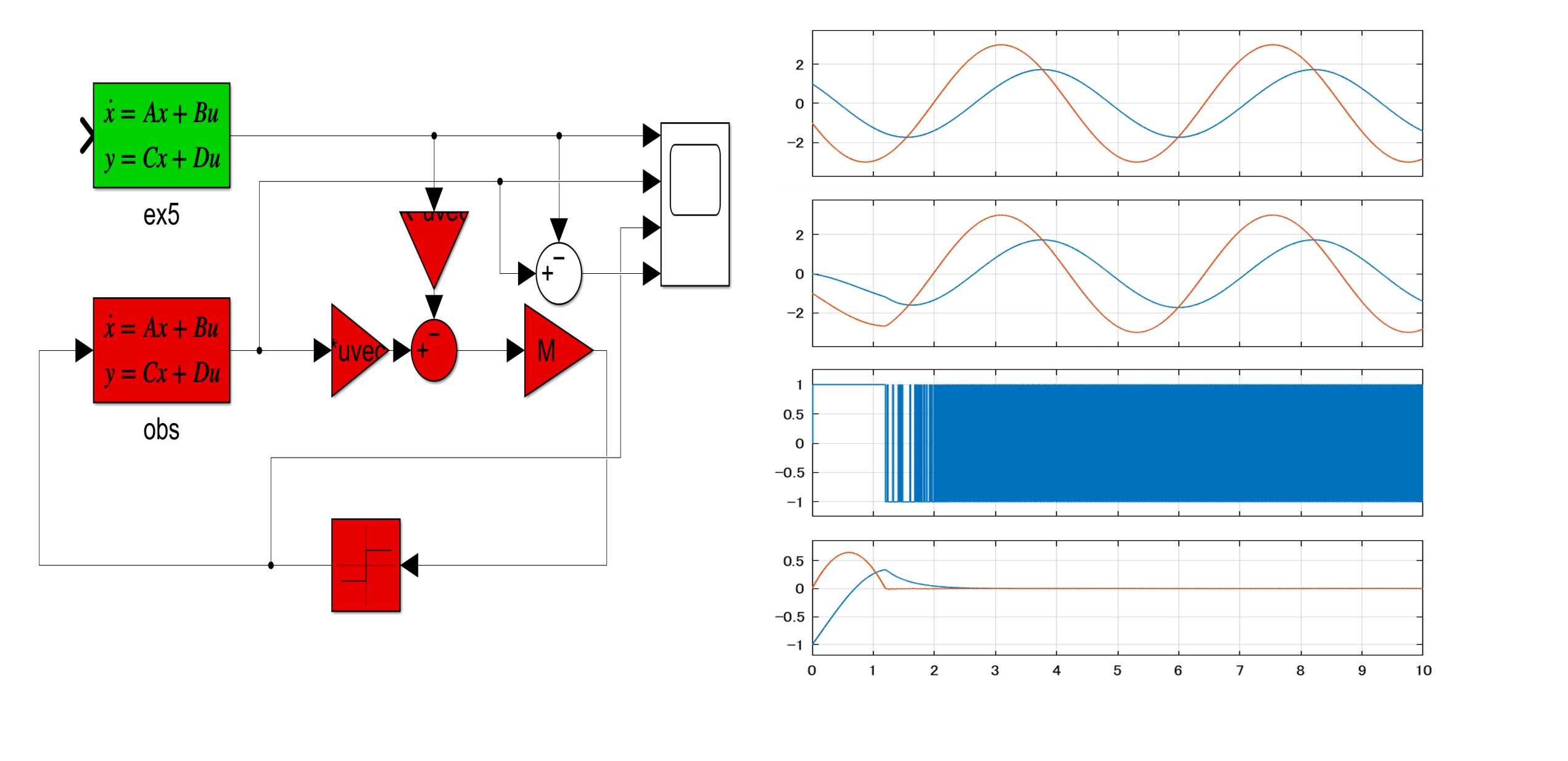
図1 Utkin’s observerのシミュレーション例