n次系の周波数応答
次の漸近安定な1入力1出力![]() 次系の状態空間表現を考えます。
次系の状態空間表現を考えます。
![]()
このとき、正弦波入力
![]()
に対する零状態応答を計算します。そのために
![]()
を、零状態応答の式
![]()
に代入して
![Rendered by QuickLaTeX.com (5)\quad \begin{array}{l} \displaystyle{y(t)=\int_0^tC\exp(A(t-\tau))Be^{j\omega\tau}d\tau}\\ \displaystyle{=C\exp(At)\int_0^te^{j\omega\tau}\exp(-A\tau)Bd\tau}\\ \displaystyle{=C\exp(At)\int_0^t\exp(j\omega\tau I_n)\exp(-A\tau)Bd\tau}\\ \displaystyle{=C\exp(At)\int_0^t\exp((j\omega I_n-A)\tau)Bd\tau}\\ \displaystyle{=C\exp(At) \left[\frac{}{}\exp((j\omega I_n-A)\tau)\right]_0^t(j\omega I_n-A)^{-1}B}\\ \displaystyle{=C\exp(At) (\exp((j\omega I_n-A)t)-I_n)(j\omega I_n-A)^{-1}B}\\ \displaystyle{=-C\exp(At)(j\omega I_n-A)^{-1}B+C\exp(At)\exp(j\omega t I_n)\exp(-At)(j\omega I_n-A)^{-1}B}\\ \displaystyle{=-C\exp(At)(j\omega I_n-A)^{-1}B+C(j\omega I_n-A)^{-1}Be^{j\omega t}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cf72e1d083b5093019ffc1a9ae42a3ca_l3.png)
ここで![]() とすると
とすると
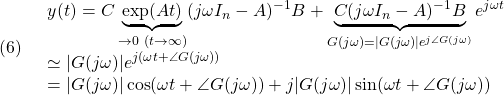
これから正弦波入力(3)に対する零状態応答は、![]() のとき次式で与えられます。
のとき次式で与えられます。
![]()
これは、入力が正弦波のときは、時間が十分立てば、出力も正弦波となることを示しています。その振幅と位相はそれぞれ![]() の絶対値と偏角となっています。
の絶対値と偏角となっています。
n次系の周波数応答
次の漸近安定な1入力1出力![]() 次系の状態空間表現を考えます。
次系の状態空間表現を考えます。
![]()
このとき、正弦波入力
![]()
に対する零状態応答を計算します。そのために
![]()
を、零状態応答の式
![]()
に代入して
![Rendered by QuickLaTeX.com (5)\quad \begin{array}{l} \displaystyle{y(t)=\int_0^tC\exp(A(t-\tau))Be^{j\omega\tau}d\tau}\\ \displaystyle{=C\exp(At)\int_0^te^{j\omega\tau}\exp(-A\tau)Bd\tau}\\ \displaystyle{=C\exp(At)\int_0^t\exp(j\omega\tau I_n)\exp(-A\tau)Bd\tau}\\ \displaystyle{=C\exp(At)\int_0^t\exp((j\omega I_n-A)\tau)Bd\tau}\\ \displaystyle{=C\exp(At) \left[\frac{}{}\exp((j\omega I_n-A)\tau)\right]_0^t(j\omega I_n-A)^{-1}B}\\ \displaystyle{=C\exp(At) (\exp((j\omega I_n-A)t)-I_n)(j\omega I_n-A)^{-1}B}\\ \displaystyle{=-C\exp(At)(j\omega I_n-A)^{-1}B+C\exp(At)\exp(j\omega t I_n)\exp(-At)(j\omega I_n-A)^{-1}B}\\ \displaystyle{=-C\exp(At)(j\omega I_n-A)^{-1}B+C(j\omega I_n-A)^{-1}Be^{j\omega t}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cf72e1d083b5093019ffc1a9ae42a3ca_l3.png)
ここで![]() とすると
とすると
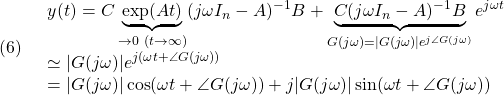
これから正弦波入力(3)に対する零状態応答は、![]() のとき次式で与えられます。
のとき次式で与えられます。
![]()
これは、入力が正弦波のときは、時間が十分立てば、出力も正弦波となることを示しています。その振幅と位相はそれぞれ![]() の絶対値と偏角となっています。
の絶対値と偏角となっています。