1. SIRモデルに基づく感染制御
1.1 SIRモデルの基礎式
感染ダイナミックスを表すSIRモデルでは、当該地域の人口![]() を
を
●![]() :感受性(susceptible)状態の人口(未感染者数)
:感受性(susceptible)状態の人口(未感染者数)
●![]() :感染性(infectious)状態の人口(感染者数)
:感染性(infectious)状態の人口(感染者数)
●![]() :回復・隔離または免疫状態(recovered/removed/immune)状態の人口(回復者数)
:回復・隔離または免疫状態(recovered/removed/immune)状態の人口(回復者数)
に分け(![]() )、これらが次の連立微分方程式に従うとします。
)、これらが次の連立微分方程式に従うとします。
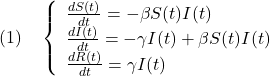
ここで、![]() は感染率、
は感染率、![]() は回復率と呼ばれます。
は回復率と呼ばれます。
いま未感染者数![]() 、感染者数
、感染者数![]() 、回復者数
、回復者数![]() の当該地域の人口
の当該地域の人口![]() に対する比率を考えると次式が成り立ちます。
に対する比率を考えると次式が成り立ちます。
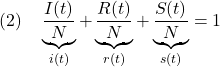
(1)と(2)から
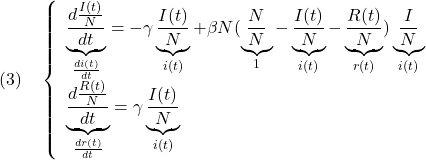
すなわち、次の正規化(無次元化)されたSIRモデルを得ます。
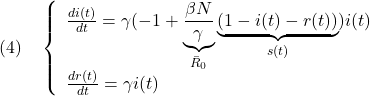
ここで、自粛率![]() を導入し、
を導入し、![]() を
を![]() に置き換えて、次式を得ます。
に置き換えて、次式を得ます。
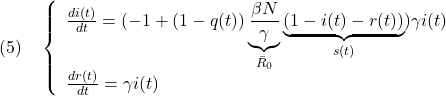
図1にSIRモデル(5)に基づく感染シミュレーションの例を示します。ただし、自粛率![]() の時系列は8割削減と5割削減を適当に設定しています(
の時系列は8割削減と5割削減を適当に設定しています(![]() は削減率と呼ばれます)。
は削減率と呼ばれます)。
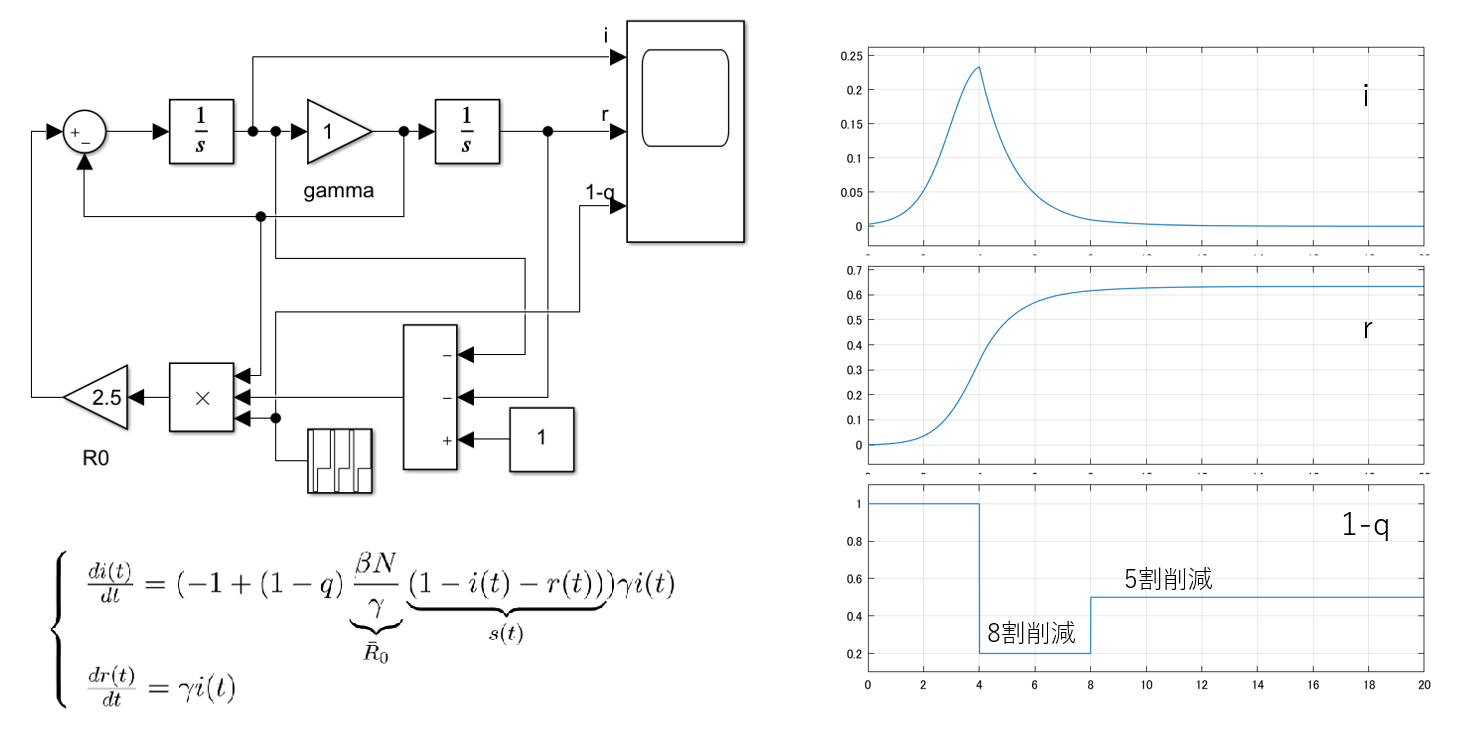 図1 正規化SIRモデルに基づく感染シミュレータの例(MATLAB/Simulink)
図1 正規化SIRモデルに基づく感染シミュレータの例(MATLAB/Simulink)
(![]() ;
; ![]() ;
; ![]() ;
; ![]() )
)
1.2 SIRモデル(全国版)に基づく感染予測
図2に全国の新規感染者数の移動平均値を示します。これに基づく基本再生産数R0の値を図3に示します。これから7/25時点でのR0の値は![]() 程度(
程度(![]() )と推測されます。
)と推測されます。
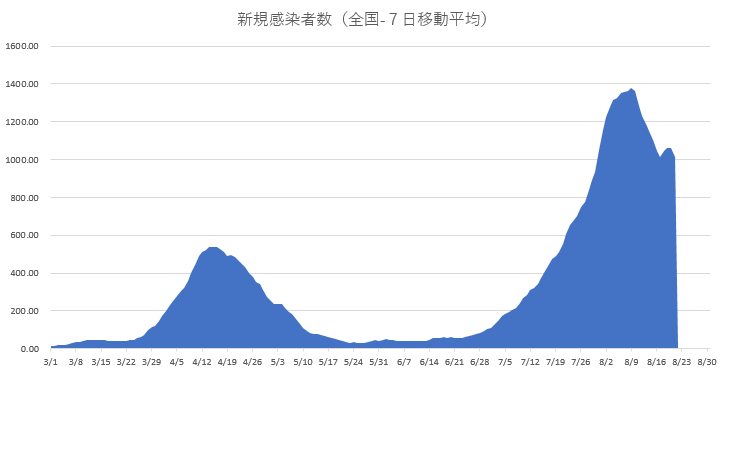 図2 全国の新規感染者数の実績値
図2 全国の新規感染者数の実績値
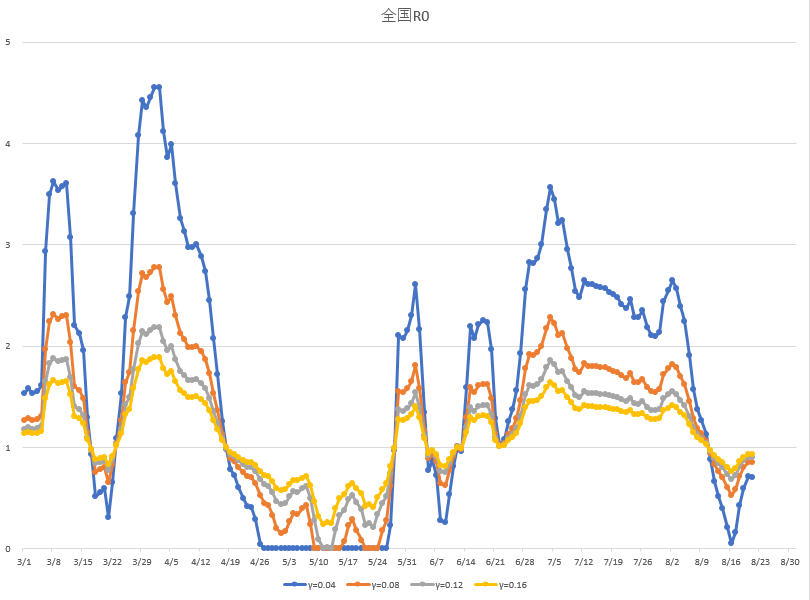 図3 全国の基本再生産数の推定値
図3 全国の基本再生産数の推定値
さらに感染予測結果を図4に示します。左図は7/1を初期時刻にとって、自粛は行われていないものとして、7/25現在の感染者数を予測したものです。右図は、7/25を初期時刻にとって、自粛率![]() を5割削減と2割削減を適当に設定して、向こう300日間の感染者数を予測したものです。新規感染者数の実績値は2000人を超えることはなかったので、もう少し厳しい自粛が行われていたと言えます。
を5割削減と2割削減を適当に設定して、向こう300日間の感染者数を予測したものです。新規感染者数の実績値は2000人を超えることはなかったので、もう少し厳しい自粛が行われていたと言えます。
 図4 SIRモデルに基づく全国の感染予測の例
図4 SIRモデルに基づく全国の感染予測の例
1.3 正規化SIRモデルに基づく感染制御
適当な累積感染者数と収束期間を実現するように自粛率![]() の時系列を制御理論を用いて導出することを考えます。(5)の行列表示は次式となります。
の時系列を制御理論を用いて導出することを考えます。(5)の行列表示は次式となります。
![]()
さらに自粛率![]() を1次遅れのダイナミックスを通して間接的に操作できるように政策変数(仮想的な操作変数)
を1次遅れのダイナミックスを通して間接的に操作できるように政策変数(仮想的な操作変数)![]() を導入します。
を導入します。
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \left\{\begin{array}{l} \left[\begin{array}{c} \dot{r}(t)\\ \dot{i}(t) \end{array}\right] =\left[\begin{array}{cc} 0 & \gamma\\ 0 & -\gamma+\gamma\bar{R}_0s(t) \end{array}\right] \left[\begin{array}{c} r(t)\\ i(t) \end{array}\right] +\left[\begin{array}{c} 0\\ -\gamma\bar{R}_0s(t)i(t) \end{array}\right]q(t)\\ \dot{q}(t)=-\frac{1}{T_q}q(t)+\frac{1}{T_q}u_q(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-14aee197f47f96f675df41632b68be6f_l3.png)
すなわち、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \left[\begin{array}{c} \dot{r}(t)\\ \dot{i}(t)\\ \dot{q}(t) \end{array}\right] =\left[\begin{array}{ccc} 0 & \gamma &0\\ 0 & -\gamma+\gamma\bar{R}_0s(t)&-\gamma\bar{R}_0s(t)i(t)\\ 0 & 0 &-\frac{1}{T_q} \end{array}\right] \left[\begin{array}{c} r(t)\\ i(t)\\ q(t) \end{array}\right] +\left[\begin{array}{c} 0\\ 0\\ \frac{1}{T_q} \end{array}\right]u_q(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-599186a53ae0fd423974aadc4f4e2e1c_l3.png)
これは2つの変動パラメータ![]() と
と![]() をもつ、次のようなLPVモデル(線形パラメータ変動モデル)とみなすことができます。
をもつ、次のようなLPVモデル(線形パラメータ変動モデル)とみなすことができます。
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{r}(t)\\ \dot{i}(t)\\ \dot{q}(t) \end{array}\right] }_{\dot{x}(t)} =\left(\underbrace{\left[\begin{array}{ccc} 0 & \gamma &0\\ 0 & -\gamma &0\\ 0 & 0 &-\frac{1}{T_q} \end{array}\right] }_{A_0} + \underbrace{\bar{R}_0s(t)}_{\alpha(t)} \underbrace{\left[\begin{array}{ccc} 0 & 0 & 0\\ 0 & \gamma & 0\\ 0 & 0 & 0 \end{array}\right] }_{A_1} \right.\\ \left.+ \underbrace{\bar{R}_0s(t)i(t)}_{\beta(t)} \underbrace{\left[\begin{array}{ccc} 0 & 0 & 0\\ 0 & 0 & -\gamma\\ 0 & 0 & 0 \end{array}\right] }_{A_2} \right) \underbrace{\left[\begin{array}{c} r(t)\\ i(t)\\ q(t) \end{array}\right] }_{x(t)} +\underbrace{\left[\begin{array}{c} 0\\ 0\\ \frac{1}{T_q} \end{array}\right] }_{B} \underbrace{u_q(t)}_{u(t)}\\ (0<\alpha(t),\beta(t)<\bar{R}_0) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a5d3c6f02f52ebb8fdc356bc6130e012_l3.png)
いま、2つの変動パラメータを適当な値に![]() と
と![]() に固定すると、次のLTIモデル(線形時不変モデル)を得ます。
に固定すると、次のLTIモデル(線形時不変モデル)を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \left[\begin{array}{c} \dot{r}(t)\\ \dot{i}(t)\\ \dot{q}(t) \end{array}\right] =\left[\begin{array}{ccc} 0 & \gamma &0\\ 0 & -\gamma+\gamma\alpha^* & -\gamma\beta^*\\ 0 & 0 &-\frac{1}{T_q} \end{array}\right] \left[\begin{array}{c} r(t)\\ i(t)\\ q(t) \end{array}\right] +\left[\begin{array}{c} 0\\ 0\\ \frac{1}{T_q} \end{array}\right]u_q(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e35e3ccf84dd4c6426f8672cff7da4e3_l3.png)
そこで、2次形式評価関数
![]()
を最小化する状態フィードバック(LQ制御則)
![]()
の効果を確かめてみます。その結果を図5に示します。左図は自粛なしの場合、右図は時刻![]() 以降、LQ制御則を適用しています。ここで、
以降、LQ制御則を適用しています。ここで、![]() 、
、![]() 、
、![]() としています。時刻
としています。時刻![]() ではすでに人口の15%(0.15
ではすでに人口の15%(0.15![]() )の感染者がいますので、強力な自粛が必要となり、
)の感染者がいますので、強力な自粛が必要となり、![]() の値は1を超える大きな値となっています。そのためシミュレータ上では飽和要素を入れてこれを制限しています。結果的にいきなり10割削減相当、いわゆるロックダウンの自粛となっています。しかし最終的な累積感染者数は9割から3割程度に抑えられています。
の値は1を超える大きな値となっています。そのためシミュレータ上では飽和要素を入れてこれを制限しています。結果的にいきなり10割削減相当、いわゆるロックダウンの自粛となっています。しかし最終的な累積感染者数は9割から3割程度に抑えられています。
 図5 正規化SIRモデルに基づく感染制御(LQ制御)の例
図5 正規化SIRモデルに基づく感染制御(LQ制御)の例
(![]() ;
; ![]() ;
; ![]() )
)
さて、![]() 、
、![]() に対する次の内分式に注目します。
に対する次の内分式に注目します。
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \begin{array}{l} \left[\begin{array}{c} \alpha(t)\\ \beta(t) \end{array}\right]= \underbrace{\frac{\alpha_2-\alpha(t)}{\alpha_2-\alpha_1}\frac{\beta_2-\beta(t)}{\beta_2-\beta_1}}_{p_{11}(\alpha(t),\beta(t))}\left[\begin{array}{c} \alpha_1\\ \beta_1 \end{array}\right]+ \underbrace{\frac{\alpha_2-\alpha(t)}{\alpha_2-\alpha_1}\frac{\beta(t)-\beta_1}{\beta_2-\beta_1}}_{p_{12}(\alpha(t),\beta(t))}\left[\begin{array}{c} \alpha_1\\ \beta_2 \end{array}\right]\\+ \underbrace{\frac{\alpha(t)-\alpha_1}{\alpha_2-\alpha_1}\frac{\beta_2-\beta(t)}{\beta_2-\beta_1}}_{p_{21}(\alpha(t),\beta(t))}\left[\begin{array}{c} \alpha_2\\ \beta_1 \end{array}\right]+ \underbrace{\frac{\alpha(t)-\alpha_1}{\alpha_2-\alpha_1}\frac{\beta(t)-\beta_1}{\beta_2-\beta_1}}_{p_{22}(\alpha(t),\beta(t))}\left[\begin{array}{c} \alpha_2\\ \beta_2 \end{array}\right] \\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6797abe598ebb6bc452731852b36f1c2_l3.png)
![]()
状態方程式(9)は、端点モデル
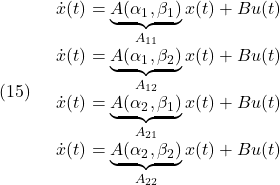
を、![]() によって重み付けして、次式のように表されます。
によって重み付けして、次式のように表されます。
![]()
このとき4つの端点モデルを安定化する状態フィードバック
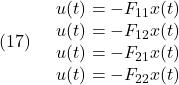
を同時安定化して求め(共通のリャプノフ関数を求め)、LPV制御則を次式で決めます。
![]()
この制御則の一例の効果を図6に示します。自粛率は1を超えることはありませんが、累積感染者数は9割から6割程度にしか抑制されていません。
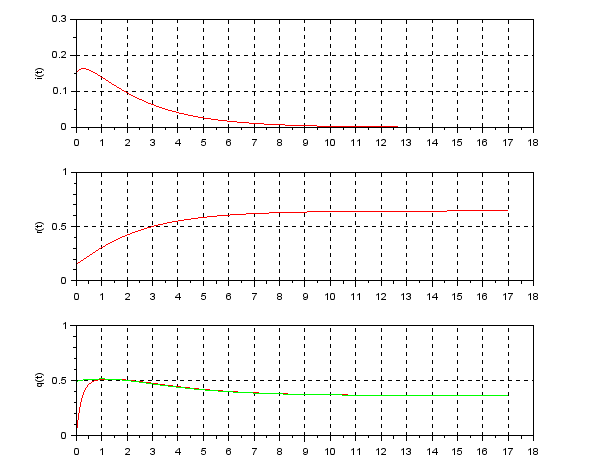 図6 正規化SIRモデルに基づく感染制御(LPV制御)の例
図6 正規化SIRモデルに基づく感染制御(LPV制御)の例
(![]() ;
; ![]() ;
; ![]() )
)
2. SIQRモデルに基づく感染制御
2.1 SIQRモデルの基礎式
SIRモデルは、次の3つの変数で表されていました。
●![]() :感受性状態の人口(未感染者数)
:感受性状態の人口(未感染者数)
●![]() :感染性状態の人口(感染者数)
:感染性状態の人口(感染者数)
●![]() :回復・隔離または免疫状態状態の人口(回復者数)
:回復・隔離または免疫状態状態の人口(回復者数)
いま、感染者数を検査の有無によって、次のように区別します(![]() )。
)。
●![]() :未検査感染性人口(市中感染者数)
:未検査感染性人口(市中感染者数)
●![]() :検査後隔離状態にある感染性人口(隔離感染者数)
:検査後隔離状態にある感染性人口(隔離感染者数)
このとき、次式で表されるSIQRモデルを考えます。
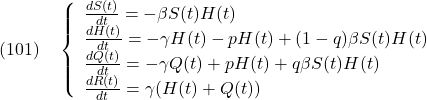
ここで、SIQRモデルの第2式と第3式は、SIRモデルの第2式を、![]() を用いて分けたものとなっています。その際、自粛率
を用いて分けたものとなっています。その際、自粛率![]() の他に隔離率
の他に隔離率![]() も導入されていることに注意してください。
も導入されていることに注意してください。![]() が日々発表される感染者数となります。
が日々発表される感染者数となります。
これら未感染者数、市中感染者数、隔離感染者数、回復者数の当該地域の人口![]() に対する比率を考えます。
に対する比率を考えます。
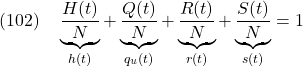
このとき
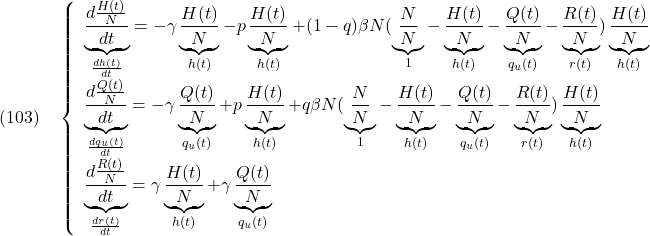
すなわち、次の正規化(無次元化)されたSIQRモデルを得ます。
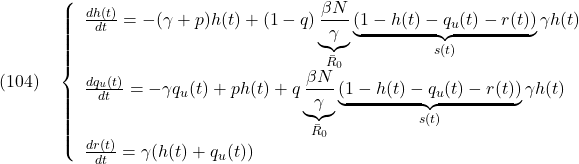
図7にSIQRモデル(104)に基づく感染シミュレーションの例を示します。ここで自粛率![]() の時系列は図1の半分にしています。これを隔離率
の時系列は図1の半分にしています。これを隔離率![]() を導入することにより、図1と同程度の感染者数に抑え込むことができています。
を導入することにより、図1と同程度の感染者数に抑え込むことができています。
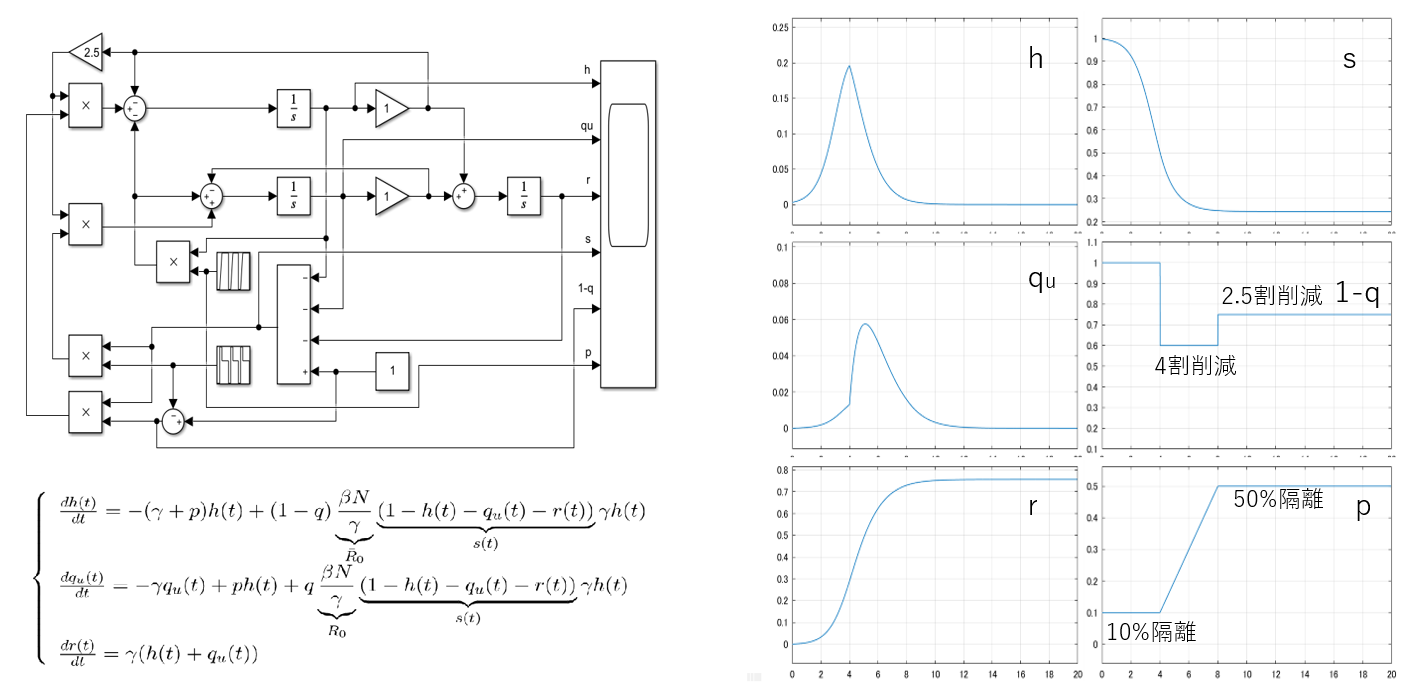 図7 正規化SIQRモデルに基づく感染シミュレータの例(MATLAB/Simulink)
図7 正規化SIQRモデルに基づく感染シミュレータの例(MATLAB/Simulink)
(![]() )
)
2.2 SIQRモデル(全国版)に基づく感染予測
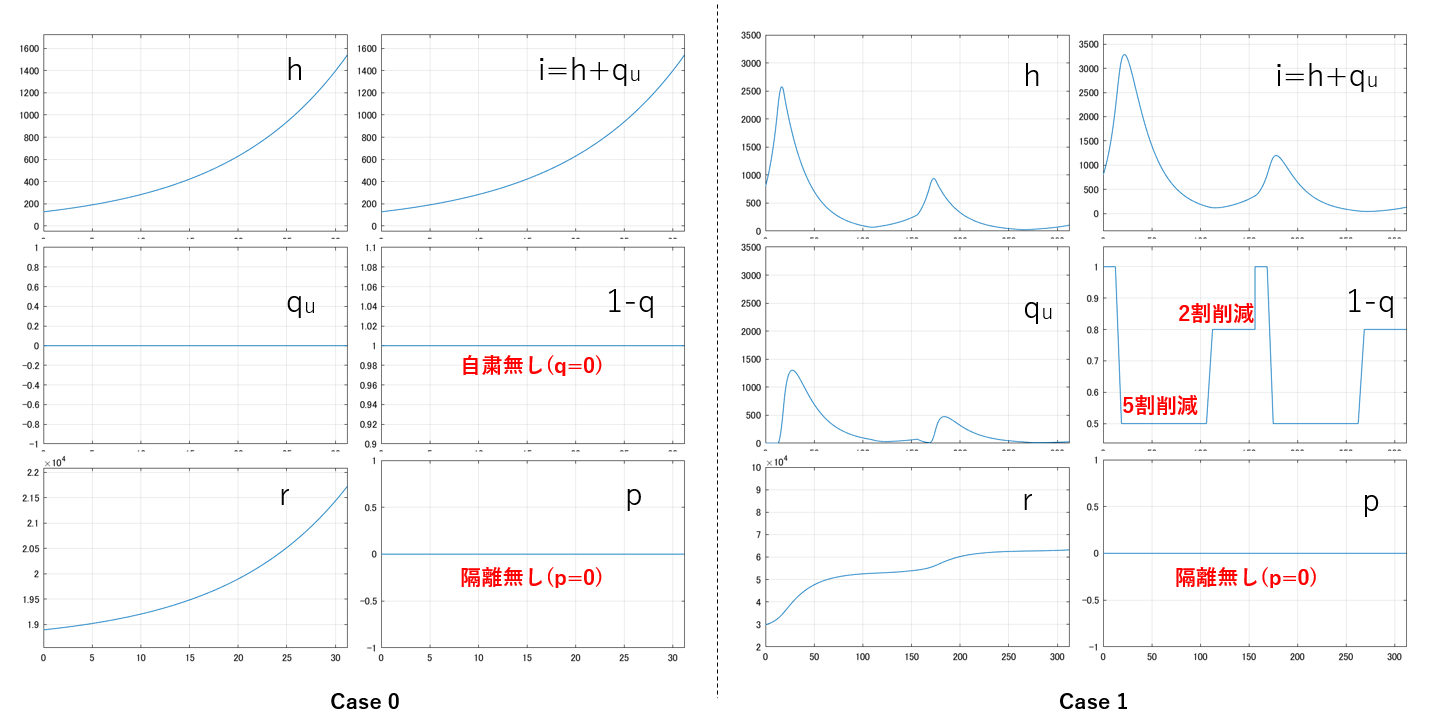
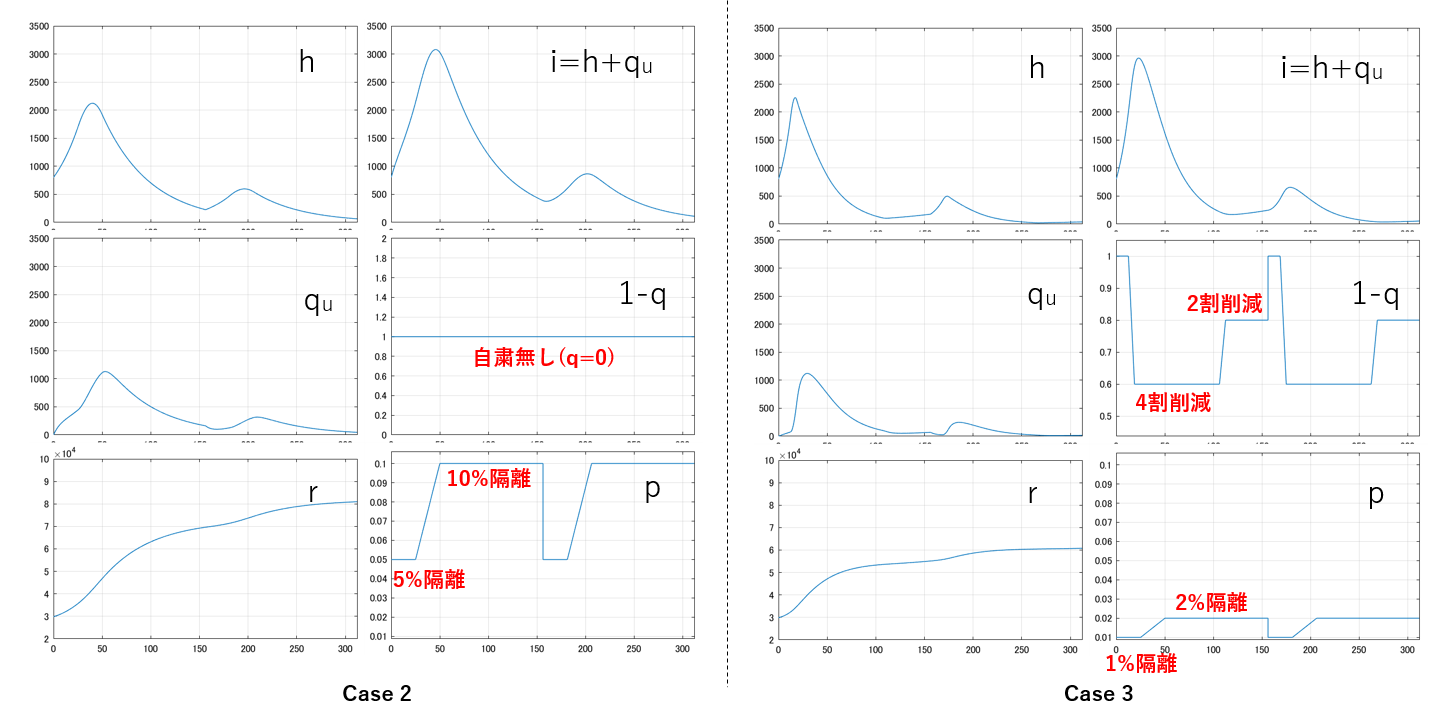 図8 SIQRモデルに基づく全国の感染予測シミュレーション
図8 SIQRモデルに基づく全国の感染予測シミュレーション
2.3 正規化SIQRモデルに基づく感染制御
適当な累積感染者数と収束期間を実現するように自粛率![]() と隔離率
と隔離率![]() の時系列を制御理論を用いて導出してみます。(104)の行列表示は次式となります。
の時系列を制御理論を用いて導出してみます。(104)の行列表示は次式となります。
![Rendered by QuickLaTeX.com (105)\quad\left[\begin{array}{c} \dot{r}(t)\\ \dot{h}(t)\\ \dot{q}_u(t) \end{array}\right] =\gamma\left[\begin{array}{ccc} 0 & 1 & 1\\ 0 & -1-\frac{p}{\gamma}+(1-q)\bar{R}_0s(t) & 0\\ 0 & \frac{p}{\gamma}+q\bar{R}_0s(t) & -1\\ \end{array}\right] \left[\begin{array}{c} r(t)\\ h(t)\\ q_u(t) \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-db1ac33e01f59035ea86270b3529f440_l3.png)
自粛率![]() と隔離率
と隔離率![]() を1次遅れのダイナミックスを通して間接的に操作できるようにそれぞれの政策変数(仮想的な操作変数)
を1次遅れのダイナミックスを通して間接的に操作できるようにそれぞれの政策変数(仮想的な操作変数)![]() と
と![]() を導入します。
を導入します。
![Rendered by QuickLaTeX.com (106)\quad\left\{\begin{array}{l} \left[\begin{array}{c} \dot{r}(t)\\ \dot{h}(t)\\ \dot{q}_u(t) \end{array}\right] =\left[\begin{array}{ccc} 0 & \gamma & \gamma\\ 0 & -\gamma+\gamma\bar{R}_0s(t) & 0\\ 0 & 0 & -\gamma\\ \end{array}\right] \left[\begin{array}{c} r(t)\\ h(t)\\ q_u(t) \end{array}\right]\\+ \left[\begin{array}{cc} 0 & 0\\ -\gamma\bar{R}_0s(t)h(t) & -1\\ \gamma\bar{R}_0s(t)h(t) & 1 \end{array}\right] \left[\begin{array}{c} q(t) \\ p(t) \end{array}\right]\\ \dot{q}(t)=-\frac{1}{T_q}q(t)+\frac{1}{T_q}u_q(t)\\ \dot{p}(t)=-\frac{1}{T_p}p(t)+\frac{1}{T_p}u_p(t) \end{array}\right.](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9171c7eb1ca480b4f202740f76c42ee8_l3.png)
すなわち、次式を得ます。
![Rendered by QuickLaTeX.com (107)\quad\begin{array}{l} \left[\begin{array}{c} \dot{r}(t)\\ \dot{h}(t)\\ \dot{q}_u(t)\\ \dot{q}(t)\\ \dot{p}(t) \end{array}\right] =\left[\begin{array}{ccccc} 0 & \gamma & \gamma&0 & 0\\ 0 & -\gamma+\gamma\bar{R}_0s(t) & 0&-\gamma\bar{R}_0s(t)h(t) & -1\\ 0 & 0 & -\gamma&\gamma\bar{R}_0s(t)h(t) & 1\\ 0&0&0&-\frac{1}{T_q}&0\\ 0&0&0&0&-\frac{1}{T_p} \end{array}\right] \left[\begin{array}{c} r(t)\\ h(t)\\ q_u(t)\\ q(t) \\ p(t) \end{array}\right]\\ +\left[\begin{array}{cc} 0&0\\ 0&0\\ 0&0\\ \frac{1}{T_q}&0\\ 0&\frac{1}{T_p} \end{array}\right] \left[\begin{array}{c} u_q(t) \\ u_p(t) \end{array}\right] \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-190fa600994dfc8bd7838ca320ee151f_l3.png)
これは2つの変動パラメータ![]() と
と![]() をもつ次のようなLPVモデル(線形パラメータ変動モデル)とみなすことができます。
をもつ次のようなLPVモデル(線形パラメータ変動モデル)とみなすことができます。