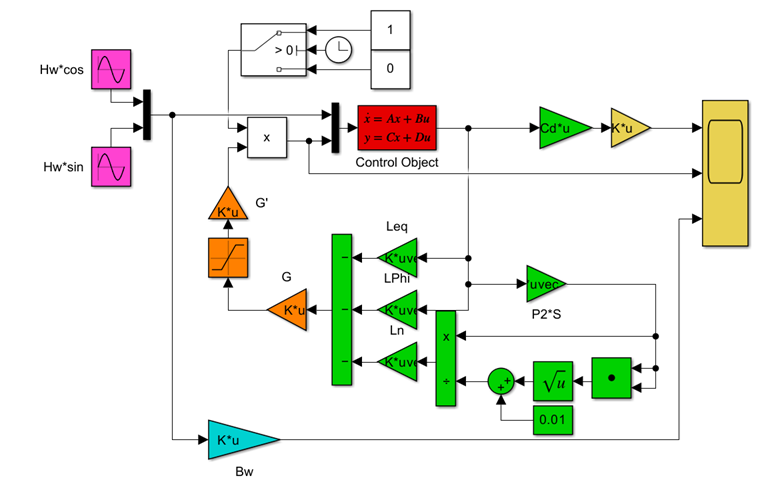
●制御対象(赤)
\left\{\begin{array}{l}
\dot{\vec x}=A(T_w){\vec x}+B(T_w)\vec{u}+B_w(T_w,\beta){\vec w},\ {\vec x}(0)={\vec x}_0\\
{\vec y}_M=C_M{\vec x}\\
y=\underbrace{C_SC_M}_{C}{\vec x}
\end{array}\right.
●外乱信号(赤紫)
{\vec w}=\left[\begin{array}{l}
H_w\sin\frac{2\pi}{T_w} t \\
H_w\cos\frac{2\pi}{T_w} t
\end{array}\right]
●SM制御則
![]()
![]()
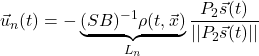
このとき、次の12ケースについて、線形シミュレーションを行ないます。ただし、短周期は![]() 、長周期は
、長周期は![]() とします。
とします。
| モデル/制御 | 横波短周期 | 横波長周期 | 斜波短周期 | 斜波長周期 |
|---|---|---|---|---|
| 2次系/SM | Case 3.1 | Case 3.2 | Case 3.3 | Case 3.4 |
| 4次系/SM | Case 3.5 | Case 3.6 | Case 3.7 | Case 3.8 |
| 6次系/SM | Case 3.9 | Case 3.10 | Case 3.11 | Case 3.12 |
|
|
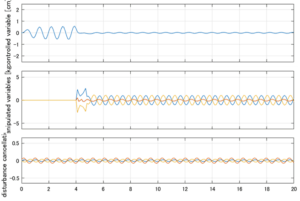
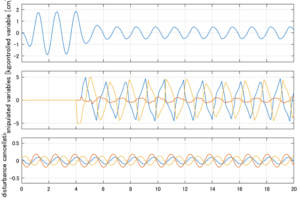
以下に、シミュレーション結果を示します。各ケースについて左図がSM制御系の応答を示しています。左図上段は制御点の応答[cm]、左図中段は操作入力[kgf]、左図下段は波浪力[kgf]を示しています。4秒までは制御なしで、4秒以降が制御ありです。制御点は横波・斜波とも右舷船首S1を取っています(横波の場合、右舷制御点の区別はありません)。また操作入力には5Vのリミッタを掛けています。
2次モデルに対するSM制御
Case 3.1(横波、短周期規則波) Case 3.1(横波、長周期規則波)
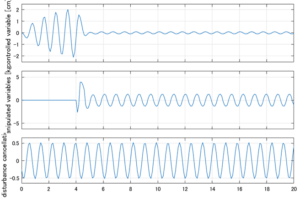
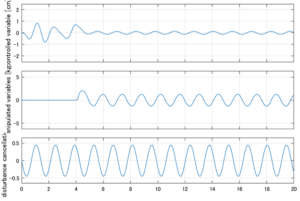
Case 3.3(斜波、短周期規則波) Case 3.4(斜波、長周期規則波)
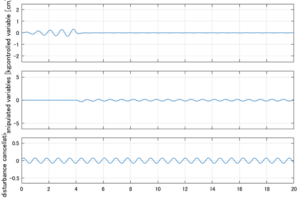
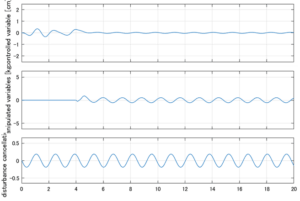
4次モデルに対するSM制御
Case 3.5(横波、短周期規則波) Case 3.6(横波、長周期規則波)
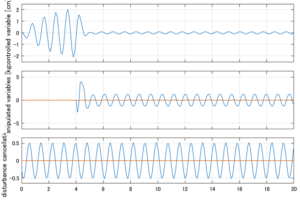
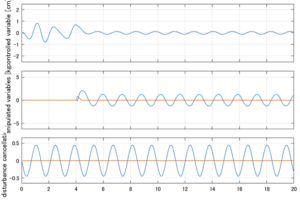
Case 3.7(斜波、短周期規則波) Case 3.8(斜波、長周期規則波)
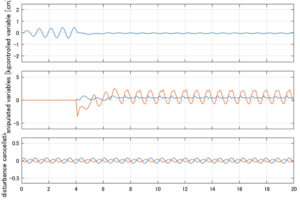
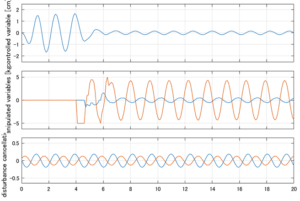
6次モデルに対するSM制御
Case 3.9(横波、短周期規則波) Case 3.10(横波、長周期規則波)
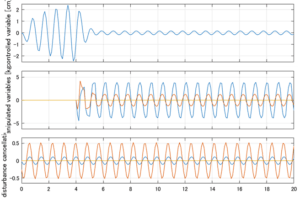
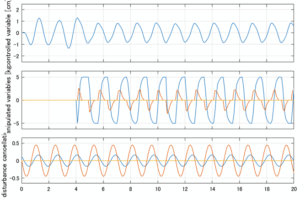
Case 3.11(斜波、短周期規則波) Case 3.12(斜波、長周期規則波)