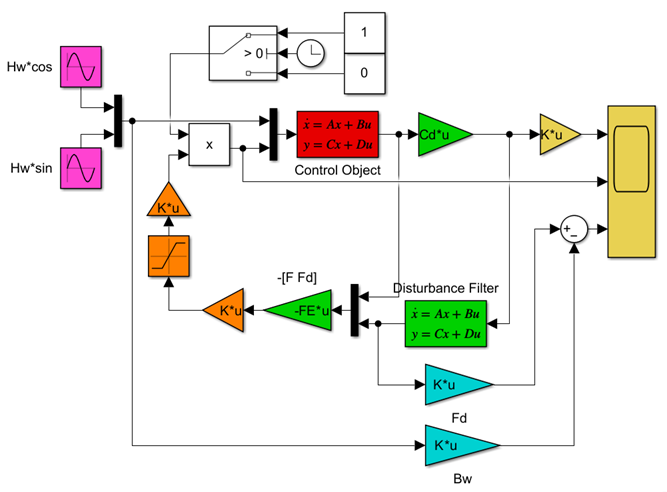
●制御対象(赤)
\left\{\begin{array}{l}
\dot{\vec x}=A(T_w){\vec x}+B(T_w)\vec{u}+B_w(T_w,\beta){\vec w},\ {\vec x}(0)={\vec x}_0\\
{\vec y}_M=C_M{\vec x}\\
y=\underbrace{C_SC_M}_{C}{\vec x}
\end{array}\right.
●外乱信号(赤紫)
{\vec w}=\left[\begin{array}{l}
H_w\sin\frac{2\pi}{T_w} t \\
H_w\cos\frac{2\pi}{T_w} t
\end{array}\right]
ここで、![]() とする。
とする。
●外乱推定に用いる観測変数(緑)
y_d=C_d{\vec x}
これは主に制御点の縦変位を取る。
●外乱フィルタ(緑)
\dot{\hat{\vec x}}_d=A_d(T_w)\hat{{\vec x}}_d+B_d(T_w){y}_d,\ \hat{x}_d(0)=0
●安定化制御則(緑)
\vec{u}=-F(T_w)\vec{x}-F_d(T_w)\hat{\vec{x}}_d
●推力配分(橙)
![]() は制御目的を達成するための望ましい
は制御目的を達成するための望ましい![]() であるが、これは4つのスラスタに次式で配分する。
であるが、これは4つのスラスタに次式で配分する。
\underbrace{\left[\begin{array}{c}F_1\\F_2\\F_3\\F_4\end{array}\right]}_{\vec F}=
\underbrace{\frac{1}{4}\left[\begin{array}{rrr} 1 & 1 & -1 \\ 1 & 1 & 1 \\ 1 & -1 & 1\\1 & -1 & -1 \end{array}\right]}_{G^\dag}
\underbrace{\left[\begin{array}{c}F_z\\F_\phi\\F_\theta\end{array}\right]}_{\vec\tau}
●推力制限(橙)
その際、次の制約が課される。
F_{min}\le F_k\le F_{max}\quad(k=1,2,3,4)
上のシミュレータは、この制約を考慮したものとなっている。ここでは、F_{max}=5[kgf]、F_{min}=-5[kgf]を用いる(要チェック)。
●留意点
制約を受けた推力は次式で駆動力に変換されるが、推力制限がある場合は設計した駆動力が働かないので注意が必要である。
\underbrace{\left[\begin{array}{c}F_z\\F_\phi\\F_\theta\end{array}\right]}_{\vec\tau}=
\underbrace{\left[\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & 1 & -1 & -1\\ -1 & 1 & 1 & -1 \end{array}\right]}_{G}
\underbrace{\left[\begin{array}{c}F_1\\F_2\\F_3\\F_4\end{array}\right]}_{\vec F}
このとき、次の16ケースについて、上のシミュレータを用いてシミュレーションを行なう。ただし、短周期は![]() 、長周期は
、長周期は![]() とする。
とする。
| モデル/制御 | 横波短周期 | 横波長周期 | 斜波短周期 | 斜波長周期 |
|---|---|---|---|---|
| 2次系/LQIM | Case 2.1 | Case 2.2 | Case 2.3 | Case 2.4 |
| 4次系/LQIM | Case 2.5 | Case 2.6 | Case 2.7 | Case 2.8 |
| 6次系/LQIM | Case 2.9 | Case 2.10 | Case 2.11 | Case 2.12 |
| 6次系/H∞IM | Case 2.13 | Case 2.14 | Case 2.15 | Case 2.16 |
|
|
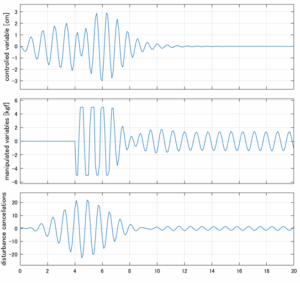
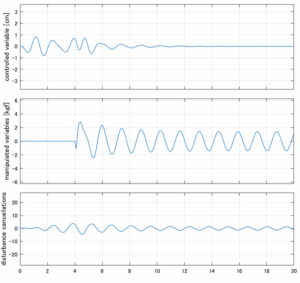
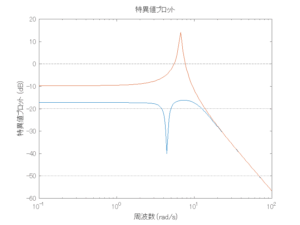
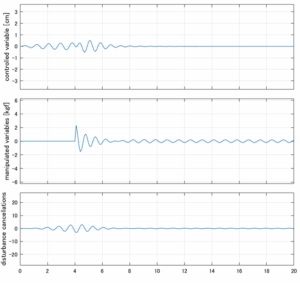
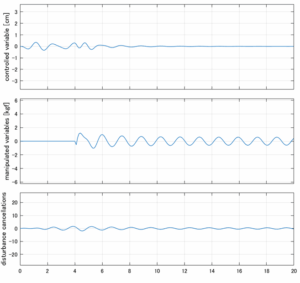
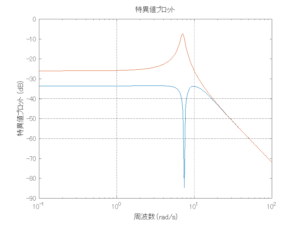
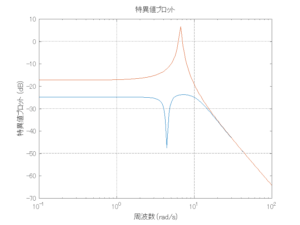
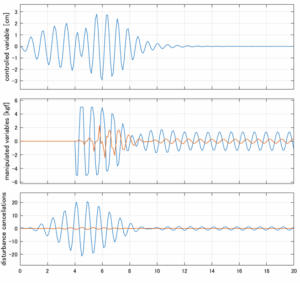
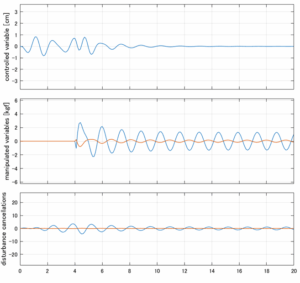
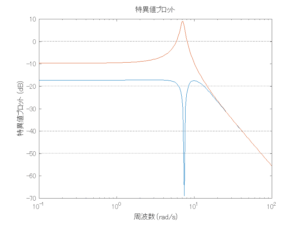
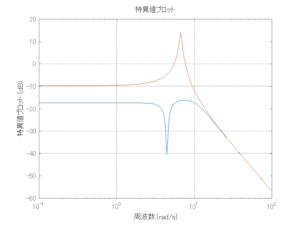
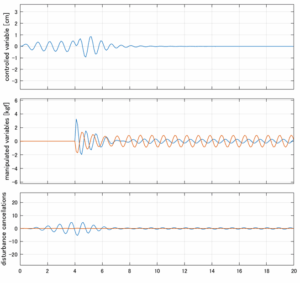
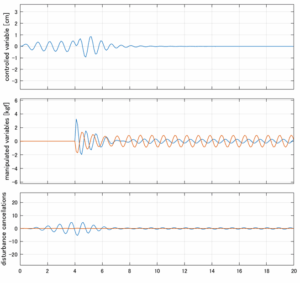
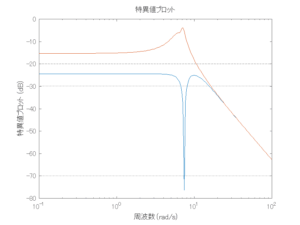
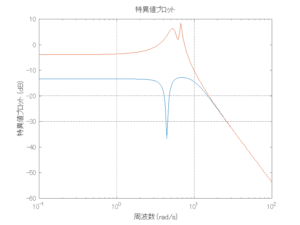
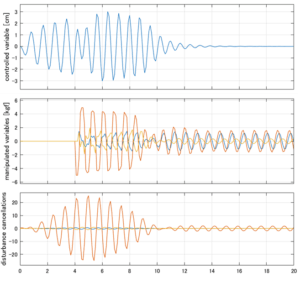
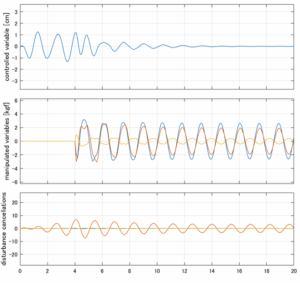
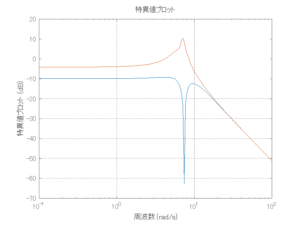
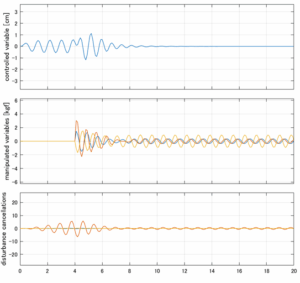
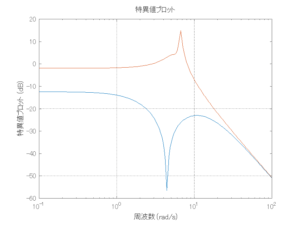
以下に、各ケースについてLQ制御系/H∞制御系の応答とゲイン線図を示す。前者の上段は制御点の応答[cm]、中段は操作入力[kgf]、下段は波浪外力[kgf]を示している。閉ループ系では
\dot{\vec x}=(A(T_w)-B(T_w)F(T_w)){\vec x}\underbrace{-B(T_w)F_d(T_w)\hat{\vec{x}}_d+B_w(T_w,\beta){\vec w}}_{相殺?}
が成り立つと思われる。左辺第2項(外乱推定項)と第3項(外乱項)が相殺するかどうかを下段で確認している。4秒までは制御なしで、4秒以降が制御ありの応答。制御点は横波・斜波とも右舷船首S1を取っている(横波の場合、右舷制御点の区別はない)。
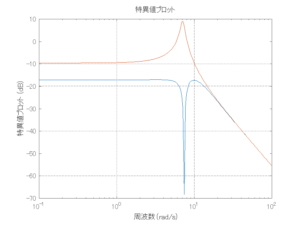
●留意点
外乱から着目する制御点までのゲイン線図は、LQIM制御系の場合、波周波数においてピンポイントで低減され、H∞IM制御系の場合、波周波数近傍で低減されている。
2次モデルに対するLQIM制御
Case 2.1(横波、短周期規則波) Case 2.2(横波、長周期規則波)
Case 2.3(斜波、短周期規則波) Case 2.4(斜波、長周期規則波)
4次モデルに対するLQIM制御
Case 2.5(横波、短周期規則波) Case 2.6(横波、長周期規則波)
Case 2.7(斜波、短周期規則波) Case 2.8(斜波、長周期規則波)
6次モデルに対するLQIM制御
Case 2.9(横波、短周期規則波) Case 2.10(横波、長周期規則波)
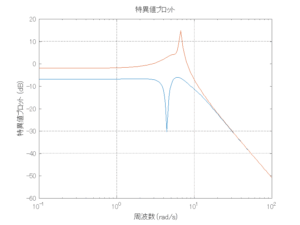
Case 2.11(斜波、短周期規則波) Case 2.12(斜波、長周期規則波)
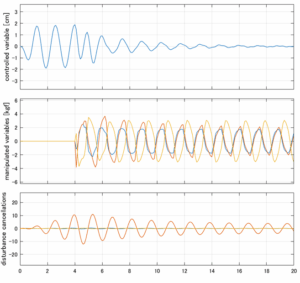
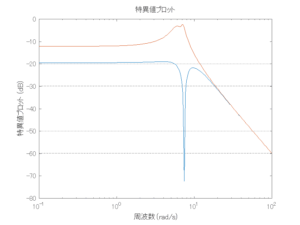
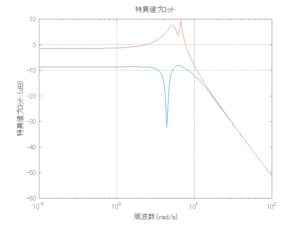
6次モデルに対するH∞IM制御
Case 2.13(横波、短周期規則波) Case 2.14(横波、長周期規則波)
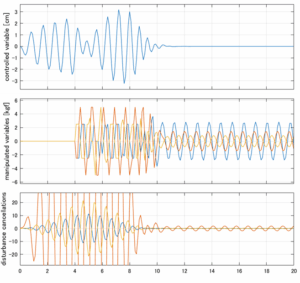
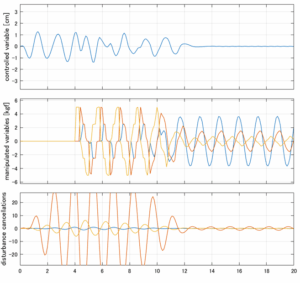
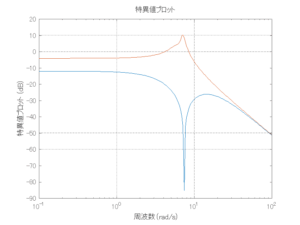
Case 2.15(斜波、短周期規則波) Case 2.16(斜波、長周期規則波)
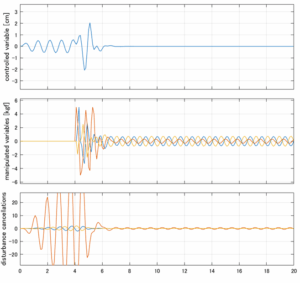
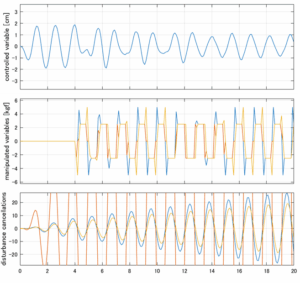
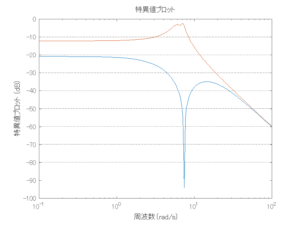
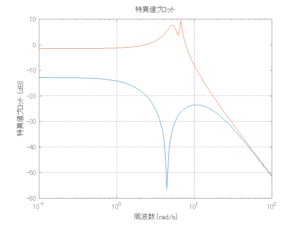
Case 2.16コメント
この場合だけ制御性能が劣化しているが、操作入力のリミッタを5Vから少し緩めたり、制御動作を4秒からでなく少し早めたりすれば、Case 2.13/14/15と同等になる。