Home Work 6.3
[P] 物理の言葉ではないと思うけど、無定位系とよばれる制御対象があるよ。モータやビークルのように、復原項がない場合は、位置が定まらないという意味らしい。無定位系では、位置についてステップ応答の実験ができないよね。
[C] 単位フィードバックを行えば、ステップ応答の実験ができるのだけど、フィードバックの知識がないと気が付かないかな。
[M] 位置と速度を状態変数にもつ無定位系
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] = \left[\begin{array}{cc} 0 & 1\\ 0 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] + \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right] u(t)\\ y(t)= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-661cd10c44d4ff35fee28f4948abb6d0_l3.png)
に対して、単位フィードバック
![]()
によって復原項を入れると、次のような2次系になるからだね。
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] = \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] + \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right] u(t)\\ y(t)= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6477ab865fc15a390483159f094f3237_l3.png)
Flipped Classroom 6.3
[1]
[2]
![]()
![]() のとき、インパルス応答を積分して、ステップ応答は次のように計算されます。
のとき、インパルス応答を積分して、ステップ応答は次のように計算されます。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \displaystyle{S(t)=\int_0^tG(\tau)d\tau=\int_0^t\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(e^{\lambda_2\tau}-e^{\lambda_1\tau})d\tau}\\ \displaystyle{= \frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}\left[\frac{e^{\lambda_2\tau}}{\lambda_2}-\frac{e^{\lambda_1\tau}}{\lambda_1}\right]_0^t}\\ \displaystyle{=\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(\frac{e^{\lambda_2t}}{\lambda_2}-\frac{e^{\lambda_1t}}{\lambda_1})-\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(\frac{1}{\lambda_2}-\frac{1}{\lambda_1})}\\ \displaystyle{=1+\frac{1}{\lambda_2-\lambda_1}(\lambda_1e^{\lambda_2t}-\lambda_2e^{\lambda_1t})} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d173fcf8b486b5642e9d12ff5b071c67_l3.png)
![]()
![]() のとき、インパルス応答を積分して、ステップ応答は次のように計算されます。
のとき、インパルス応答を積分して、ステップ応答は次のように計算されます。
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \displaystyle{S(t)=\int_0^tG(\tau)d\tau=\int_0^t\lambda^2\tau e^{\lambda\tau}d\tau}\\ \displaystyle{=\lambda^2\left[\tau \frac{1}{\lambda}e^{\lambda\tau}\right]_0^t -\lambda^2\int_0^t \frac{1}{\lambda}e^{\lambda\tau}d\tau}\\ \displaystyle{=\lambda te^{\lambda t}-\lambda\left[\frac{1}{\lambda}e^{\lambda\tau}\right]_0^t}\\ \displaystyle{=1+(\lambda t-1)e^{\lambda t}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a118c65350e9a4f5d018ff031436c980_l3.png)
![]()
![]() のとき、インパルス応答を積分して、公式
のとき、インパルス応答を積分して、公式
![]()
を用いて、ステップ応答は次のように計算されます。
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \displaystyle{S(t)=\int_0^tG(\tau)d\tau=\int_0^t\frac{\omega_n^2}{\lambda_I}e^{\lambda_R\tau}\sin\lambda_I \tau d\tau}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}\left[ \frac{e^{\lambda_R\tau}}{\lambda_R^2+\lambda_I^2}(\lambda_R\sin\lambda_I\tau-\lambda_I\cos\lambda_I\tau)\right]_0^t}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}\frac{1}{\omega_n^2} (e^{\lambda_Rt}(\lambda_R\sin\lambda_It-\lambda_I\cos\lambda_It)+\lambda_I)}\\ \displaystyle{=1-\frac{\omega_n}{\lambda_I}e^{\lambda_Rt} (\sin\lambda_It\times\frac{-\lambda_R}{\omega_n}+\cos\lambda_It\times\frac{\lambda_I}{\omega_n})}\\ \displaystyle{=1-\frac{\omega_n}{\lambda_I}e^{\lambda_Rt} (\sin\lambda_It\cos\phi+\cos\lambda_It\sin\phi)}\\ \displaystyle{=1-\frac{\omega_n}{\lambda_I}e^{\lambda_Rt}\sin(\lambda_It+\phi) \quad(\phi=\tan^{-1}\frac{\lambda_I}{-\lambda_R})} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3793ae4ad3dcc7b944a94325418dafe8_l3.png)
[3]
ヒントより、![]() だから
だから
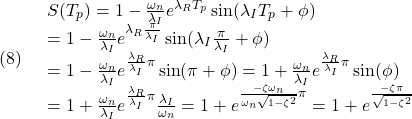
[4]
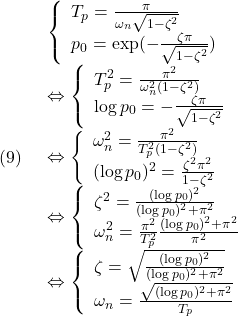
[5]