| 【本章のねらい】 ・伝達関数行列に対応する状態空間表現(実現)を求める。 ・実現の可制御可観測な部分系を取り出して,与えられた伝達関数行列に対応する最小実現を求める。 |
8.1 実現問題
| 状態空間表現
から伝達関数行列表現
を求める計算を,つぎのドイルの記法を用いて表す。
ここでは,逆に伝達関数行列表現(8.2)から状態空間表現(8.1)を求める問題、
を満足する行列
また,1入力1出力系の場合は,
以下では,まず1入力1出力系の場合を考える。1次系について,次式が成り立つ。
2次系について,次式が成り立つ。
ここで,(8.8)式の2つの実現は,
について,(8.5)式の関係にある。また,(8.9)式は(8.8)式を(8.6)式の意味で転置したものである。 一般に,1入力1出力
|
*分子多項式の次数が分母多項式の次数を超えない場合をいう。
**『線形システム制御入門』の8.1節のファディーブの公式を用いて証明できる。
| 例題8.1 むだ時間要素
このとき,対応する状態空間表現の一つを求めよ。 解答 |
| 演習8.1 むだ時間伝達関数のつぎの近似式に対応する状態空間表現の一つを求めよ。
|
| 以上の1入力1出力系の実現を利用して,多入力出力系の場合の実現の一つを求める方法を考える。
の各要素の実現を
とするとき,
で与えられる。ここで
は,サイズ
は,サイズ
は,サイズ
は,サイズ ちなみに,
の可制御な実現の一つは
また,可観測な実現の一つは
で与えられる。 |
| 例題8.2 つぎの1入力2出力伝達関数行列の実現を一つ求めよ。
解答
だから
となる。 |
| 演習8.2 つぎの2入力1出力伝達関数行列の実現を一つ求めよ。
|
8.2 最小実現
| 前節で求めた伝達関数行列の実現は,最小次元数をもつとは限らない。ここでは,最小次元数をもつ実現,すなわち最小実現を求める方法を考える。
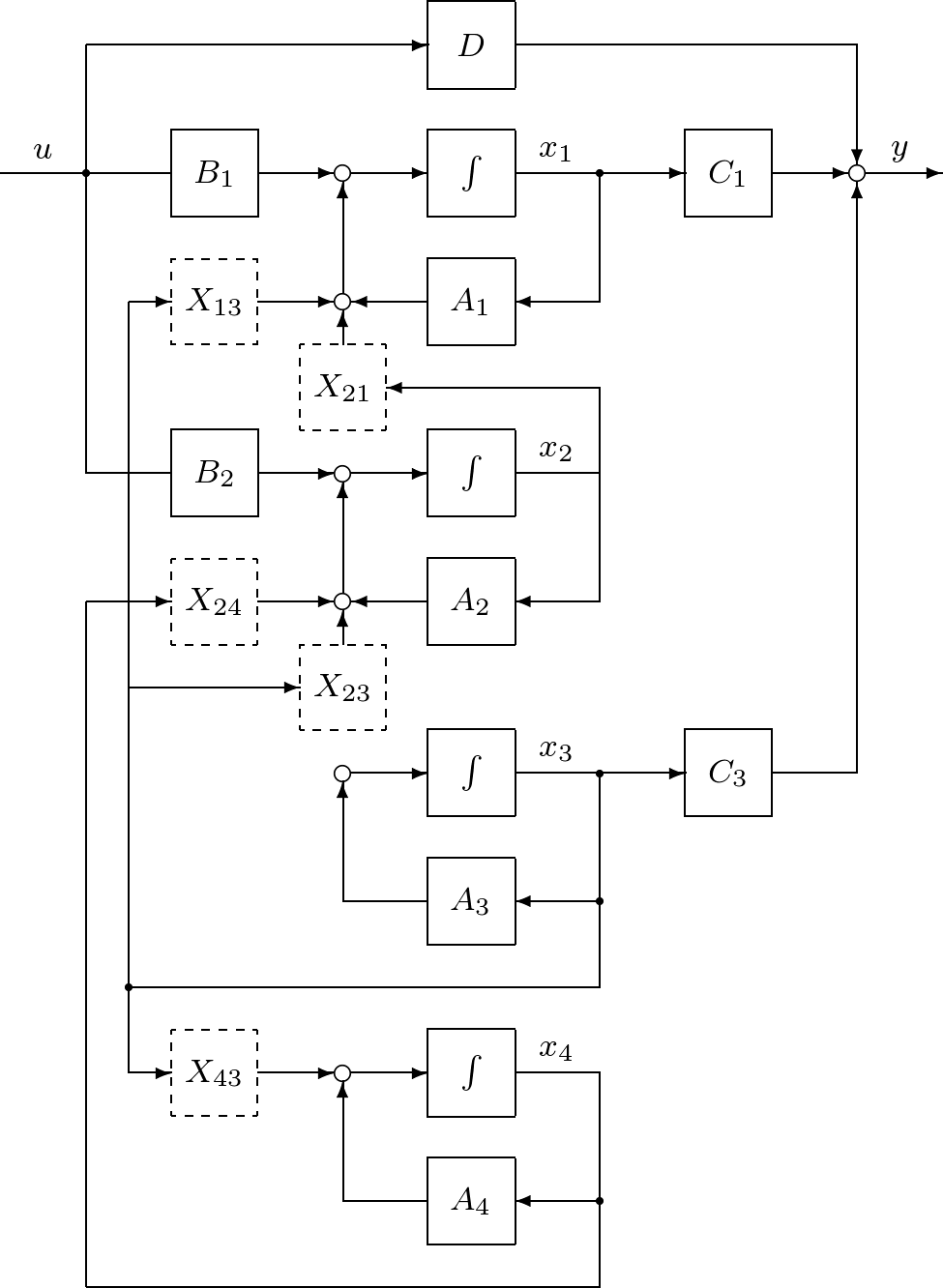
一般に,不可制御かつ不可観測な状態空間表現(8.1)は適当な座標変換により,つぎの正準構造をもつように変換できることが知られている。
ここで,正方行列
さて,(8.23)を表す伝達関数行列を
これが最小実現であることが知られている。すなわち,最小実現は,可制御かつ可観測な部分系であり,入力から出力までの伝達特性を表している。 最小実現の計算は,まず,正準構造の可制御な部分系
を求め,この可観測な部分系として求めるか,または,正準構造の可観測な部分系
を求め,この可制御な部分系として求めればよい。したがって,可制御な部分系または可観測な部分系の計算が基礎となる。 一般に,つぎのように変換する直交行列
ここで, そのような直交行列 |
| /*staircase.m*/ function [T,m]=staircase(A,B,tol) [n,r]=size(B); j=0; s=0; T=eye(n); B1=B; A1=A; while j j=j+1; [U1,S1,V1]=svd(B1); m(j)=rank(B1,tol); if (m(j)==n-s)|(m(j)==0),k=j; break, end W=[eye(s) zeros(s,n-s); zeros(n-s,s) U1 ]; T=T*W; A1=W’*A1*W; s=s+m(j); B1=A1(s+1:n,s-m(j)+1:s); end |
| ここで,tol は,7行で有効階数 m(j) を決めるために適切に選ばれる零判定基準である。
同様に,つぎのように変換する直交行列
ここで, そのような直交行列を求める階段化アルゴリズムを実行するMファイルの作成例をつぎに示す。 |
| %staircase2.m function [T,p]=staircase2(A,C,tol) [T,p]=staircase(A’,C’,tol) |
| 例題8.3 例題8.2で得た実現の可制御かつ可観測な部分系を求め,最小実現を得よ。
解答 Mファイル |
| %min_realization.m A=[-1 0 0;0 -3 -2; 0 1 0]; B=[1;1;0]; C=[1 0 0;0 1 1]; D=[0;0]; [T,m]=staircase(A,B,0.01); AA=T’*A*T; BB=T’*B; CC=C*T; n=sum(m); sys=ss(AA(1:n,1:n),BB(1:n:),CC(:1:n),D); tf(sys) |
| を実行して,
を得る。このとき
となる。この可制御部分を取り出すと
となり,しかもこれは可観測であるので最小実現である。 |
| 演習8.3 演習8.2で得た実現の可制御かつ可観測な部分系を求め,最小実現を得よ。 |
演習問題の解答
| 【演習8.1】 から,実現の一つは
である。 |
【演習8.2】![Rendered by QuickLaTeX.com \frac{s+2}{s^2+3s+2} = \left[\begin{array}{cc|c} -3 & -2 &1 \\ 1 & 0 & 0 \\\hline 1 & 2 & 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-02a700ac2acf1e2c1c049368c35a65e4_l3.png) , ,だから
を得る。 |
| 【演習8.3】Mファイル |
| %min_realization2.m A=[-3 -2 0;1 0 0; 0 0 -2]; B=[1 0;0 0;0 1]; C=[1 2 1]; D=[0 0]; [T,m]=staircase(A,B,0.01); AA=T’*A*T; BB=T’*B; CC=C*T; n=sum(m); sys=ss(AA(1:n,1:n),BB(1:n:),CC(:1:n),D); tf(sys) |
| を実行して,
を得る。このとき
となる。この可観測部分を取り出すと
となり,しかもこれは可制御であるので最小実現である。 |
![Rendered by QuickLaTeX.com \displaystyle{(8.8)\quad = \left[\begin{array}{cc|c} -a_1 & -a_2 & 1 \\ 1 & 0 & 0 \\\hline b_1 & b_2 & d \end{array}\right] = \left[\begin{array}{cc|c} 0 & 1 & 0 \\ -a_2 & -a_1 & 1 \\\hline b_2 & b_1 & d \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d7a3af5f4f8e549e8d5b0bc925920021_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.9)\quad = \left[\begin{array}{cc|c} -a_1 & 1 & b_1 \\ -a_2 & 0 & b_2 \\\hline 1 & 0 & d \end{array}\right] = \left[\begin{array}{cc|c} 0 & -a_2 & b_2 \\ 1 & -a_1 & b_1 \\\hline 0 & 1 & d \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-346bd4535c305aab672d107228824443_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \left[\begin{array}{cccc|c} -a_1 & \cdots & -a_{n-1} & -a_n & 1 \\ 1 & \cdots & 0 & 0 & 0 \\ \vdots & \ddots & \vdots & \vdots & 0 \\ 0 & \cdots & 1 & 0 & 0 \\ \hline b_1 & \cdots & b_{n-1} & b_n & d \\ \end{array}\right] = \left[\begin{array}{cccc|c} 0 & 1 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & 0 \\ 0 & 0 & \cdots & 1 & 0 \\ -a_n & -a_{n-1} & \cdots & -a_1 & 1 \\ \hline b_n & b_{n-1} & \cdots & b_1 & d \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1182e60b321b80d67da72737cf93a6aa_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \left[\begin{array}{cccc|c} -a_1 & 1 & \cdots & 0 & b_1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ -a_{n-1} & 0 & \cdots & 1 & b_{n-1} \\ -a_n & 0 & \cdots & 0 & b_n \\\hline 1 & 0 & \cdots & 0 & 0 \end{array}\right]\ = \left[\begin{array}{cccc|c} 0 & \cdots & 0 & -a_n & b_n \\ 1 & \cdots & 0 & -a_{n-1} & b_{n-1} \\ \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & \cdots & 1 & -a_1 & b_1 \\\hline 0 & \cdots & 0 & 1 & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d5720a8829c9dfa241b03305b3b25411_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.11)\quad G(s)= \left[\begin{array}{cccc} G_{11}(s) & \cdots & G_{1m}(s) \\ \vdots & \ddots & \vdots \\ G_{p1}(s) & \cdots & G_{pm}(s) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7cb240795c5097204412352dfb980d8a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.13)\quad \left[\begin{array}{cccc} G_{11}(s) & \cdots & G_{1m}(s) \\ \vdots & \ddots & \vdots \\ G_{p1}(s) & \cdots & G_{pm}(s) \end{array}\right] = \left[\begin{array}{ccc|ccc} A_1 & \cdots & 0 & B_{1} \\ \vdots & \ddots & \vdots & \vdots \\ 0 & \cdots & A_p & B_{p} \\\hline C_{1} & \cdots & C_{p} & D \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d7220fda434ac07c20e2c4bea4de023f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.14)\quad A_i= \left[\begin{array}{ccc} A_{i1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & A_{im} \end{array}\right] \ (i=1,\cdots,p) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-97d82178ac1ef7da5b4a4804aa5733aa_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.15)\quad B_i= \left[\begin{array}{ccc} B_{i1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & B_{im} \end{array}\right] \ (i=1,\cdots,p) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-411bfaa56e8913f1d700b91bb4fb8318_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.16)\quad C_i= \left[\begin{array}{ccc} C_{i1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & C_{im} \end{array}\right] \ (i=1,\cdots,p) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-229691483d6d651a5baff611990e829b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.17)\quad D= \left[\begin{array}{ccc} D_{11} & \cdots & D_{1m} \\ \vdots & \ddots & \vdots \\ D_{p1} & \cdots & D_{pm} \end{array}\right] \ (i=1,\cdots,p) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-26d78920b61bbc58ffebe39615ed38bd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.19)\quad G(s)&=& \left[\begin{array}{cccc|c} -a_1I_m & \cdots & -a_{n-1}I_m & -a_nI_m & I_m \\ I_m & \cdots & 0 & 0 & 0 \\ \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & \cdots & I_m & 0 & 0 \\\hline G_1 & \cdots & G_{n-1} & G_n & D \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2147338b5b2e2e48c7ca64d574ff9446_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.20)\quad &=& \left[\begin{array}{cccc|c} 0 & I_m & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & I_m & 0 \\ -a_nI_m & -a_{n-1}I_m & \cdots & -a_1I_m & I_m \\\hline G_n & G_{n-1} & \cdots & G_1 & D \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f4b3e34a1cb231f0c99ea3fcdddb6b69_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.21)\quad G(s)&=& \left[\begin{array}{cccc|c} -a_1I_p & I_p & \cdots & 0 & G_1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ -a_{n-1}I_p & 0 & \cdots & I_p & G_{n-1} \\ -a_nI_p & 0 & \cdots & 0 & G_n \\\hline I_p & 0 & \cdots & 0 & D \end{array}\right]\ }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6978afaef8daedb2ce9dccb7a11256cd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.22)\quad &=& \left[\begin{array}{cccc|c} 0 & \cdots & 0 & -a_nI_p & G_n \\ I_p & \cdots & 0 & -a_{n-1}I_p & G_{n-1} \\ \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & \cdots & I_p & -a_1I_p & G_1 \\\hline 0 & \cdots & 0 & I_p & D \end{array}\right]\ }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-025c74ce69e17aa7f048aa587bdca393_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \frac{s+1}{s^2+3s+2} = \left[\begin{array}{cc|c} -3 & -2 & 1 \\ 1 & 0 & 0 \\\hline 1 & 1 & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-820089b2535805b0088531f9b06f3193_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ G(s)= \left[\begin{array}{ccc|c} -1 & 0 & 0 & 1 \\ 0 & -3 & -2 & 1\\ 0 & 1 & 0 & 0 \\\hline 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-238da7f8aef65560e4a36b8bccfed84f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.23)\quad \left[\begin{array}{c|c} TAT^{-1} & TB \\\hline CT^{-1} & D \end{array}\right] = \left[\begin{array}{cccc|c} A_1 & 0 & X_{13} & 0 & B_1 \\ X_{21} & A_2 & X_{23} & X_{24} & B_2 \\ 0 & 0 & A_3 & 0 & 0 \\ 0 & 0 & X_{43} & A_4 & 0 \\\hline C_1 & 0 & C_3 & 0 & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aca4fee72af4083324246c35ea634544_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.25)\quad \left[\begin{array}{cc|c} A_1 & 0 & B_1 \\ X_{21} & A_2 & B_2 \\\hline C_1 & 0 & 0 \end{array}\right]=G(s) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fd69efff248bd3d7a38c87a6a5d2be09_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.26)\quad \left[\begin{array}{cc|c} A_1 & X_{13} & B_1 \\ 0 & A_3 & 0 \\\hline C_1 & C_3 & 0 \end{array}\right]=G(s) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1abfe9504b1b05046e408992203637e4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.27)\quad \left[\begin{array}{c|c} T^TAT & T^TB \\\hline CT & D \end{array}\right] = \left[\begin{array}{ccccc|c} A_1 & X & \cdots & X & X & B_1 \\ B_2 & A_2 & \cdots & X & X & 0 \\ 0 & \ddots & \ddots & \vdots & \vdots & \vdots \\ \vdots & \ddots & B_{k-1} & A_{k-1} & X & 0 \\ 0 & \cdots & 0 & B_k & A_k & 0 \\\hline X & X & \cdots & X & X & D \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bebfa6a7ec1e3d3439827215b71906b0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.28)\quad \left[\begin{array}{c|c} T^TAT & T^TB \\\hline CT & D \end{array}\right] = \left[\begin{array}{ccccc|c} A_1 & C_2 & \cdots & 0 & 0 & X \\ X & A_2 & \ddots & \vdots & \vdots & \vdots \\ \vdots & \vdots & \ddots & C_{k-1} & 0 & X \\ X & X & \cdots & A_{k-1} & C_k & X \\ X & X & \cdots & X & A_k & X \\\hline C_1 & 0 & \cdots & 0 & 0 & D \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6ceafd83a60c165e75fa6ea4fd8f23d0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ T= \left[\begin{array}{ccc} -0.7071 & 0.5774 & -0.4082 \\ -0.7071 & -0.5774 & 0.4082 \\ 0 & 0.5774 & 0.8165 \end{array}\right], \ m_1=1,\ m_2=1,\ m_3=0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-92e087299ea77ed3a043849cc9d65e7f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c|c} T^TAT & T^TB \\\hline CT & D \end{array}\right] = \left[\begin{array}{ccc|c} -2.0000 & -0.0000 & 1.7321 & -1.4142 \\ -1.2247 & -1.0000 & 2.1213 & 0 \\ 0 & 0 & -1.0000 & 0 \\\hline -0.7071 & 0.5774 & -0.4082 & 0 \\ -0.7071 & 0 & 1.2247 & 0 \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d9e9c93cf1d7970d3a1ea2722b808e91_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ G(s)= \left[\begin{array}{cc|c} -2.0000 & -0.0000 & -1.4142\\ -1.2247 & -1.0000 & 0\\\hline -0.7071 & 0.5774 & 0\\ -0.7071 & 0 & 0\\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f66d12e6d25d761cc6ef7e5a4317680b_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{cc|c} 0 & 1 & 0 \\ -\frac{12}{L^2} & -\frac{6}{L} & 1 \\\hline 0 & -\frac{12}{L} & 1 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8791b10c9e8d24f0e89ba1c36b7e8e1d_l3.png)
![Rendered by QuickLaTeX.com G(s)= \left[\begin{array}{ccc|cc} -3 & -2 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & -2 & 0 & 1\\\hline 1 & 2 & 1& 0 & 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-53234bc4586d74cb92e6abe08b23456c_l3.png)
![Rendered by QuickLaTeX.com T= \left[\begin{array}{ccc} -0.4082 & -0.1826 & -0.8944 \\ -0.8165 & -0.3651 & 0.4472 \\ -0.4082 & 0.9129 & 0.0000 \\ \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-13752e35a12134b463334aaadd894e68_l3.png) ,
,![Rendered by QuickLaTeX.com \left[\begin{array}{c|c} T^TAT & T^TB \\\hline CT & D \end{array}\right] = \left[\begin{array}{ccc|cc} -1.1667 & 0.3727 & -0.0000 & -0.4082 & -0.4082 \\ 0.3727 & -1.8333 & -0.0000 & -0.1826 & 0.9129 \\ -2.7386 & -1.2247 & -2.0000 & -0.8944 & 0.0000 \\\hline -2.4495 & 0 & -0.0000 & 0 & 0 \\ \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aeba8d0214bb2b2cf70900ced32e9e6e_l3.png)
![Rendered by QuickLaTeX.com G(s)= \left[\begin{array}{cc|cc} -1.1667 & 0.3727 & -0.4082 & -0.4082 \\ 0.3727 & -1.8333 & -0.1826 & 0.9129 \\\hline -2.4495 & 0 & 0 & 0 \\ \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8aef9bf8d730cb671be66a87e3fdd8f7_l3.png)