|
【本章のねらい】 ・1次系,2次系の状態フィードバックの最適設計を,リッカチ方程式を解いて行う。 ・ リッカチ方程式を解くMファイルを理解し,これを用いて高次系の状態フィードバックの最適設計を行なう。 ・ オブザーバベースト・コントローラの最適設計を,リッカチ方程式CAREを解いて状態フィードバックを,またリッカチ方程式FAREを解いてオブザーバゲインを求めて行う。 |
5.1 状態フィードバックの最適設計
|
可制御な
を安定化する状態フィードバック
の決定法を改めて考える。一つの方法は,閉ループ系
の時間応答に関する評価規範として,2次形式評価関数
を設定し,これを最小化する問題を解くことである。ただし,
の解
|
|
まず,1次系の場合を考える。
例題5.1 時定数
に対して,評価関数
を最小にするように,状態フィードバック
の解
|
演習5.1 例題5.1において,![]() ,
,![]() とする。このとき,つぎの重み係数をもつ評価関数を最小にする
とする。このとき,つぎの重み係数をもつ評価関数を最小にする![]() を決定せよ。
を決定せよ。
(1) ![]() ,
,
(2) ![]() ,
,
(3) ![]()
また,![]() のとき,閉ループ系の時間応答をMATLABでシミュレーションせよ。
のとき,閉ループ系の時間応答をMATLABでシミュレーションせよ。
|
つぎに,2次系の場合を考える。
例題5.2 2次系
を安定化する状態フィードバック
を最小にするように求めよ。
を要素ごとに整理して
を得る。これは,まず第1式より
ここで,(1)だけが,
|
演習5.2 つぎの2次系について,例題5.2と同じ問題設定で解け。
![]()
![]()
|
例題5.3 2次系
を安定化する状態フィードバック
を最小にするように求めると
となることを示せ。
を要素ごとに整理して
を得る。まず,第1式より
と求まる。つぎに,第3式より
となるが,
でなければならない。さらに,第2式より
となるが,
でなければならない。このとき
|
演習5.3 2次系
![]()
について,例題5.3と同じ問題設定で解くと
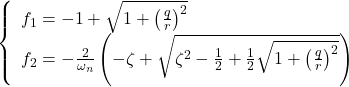
のように与えられることを示せ。
|
ちなみに,例題5.3において,評価関数
を最小にするように求めると
となる。演習5.3においては
となる。これらから重み係数 |
|
さて,リッカチ方程式を計算機を用いて解くときは,ハミルトン行列
のように求めて,状態フィードバックゲインを
によって得る。 |
|
例題5.4 リッカチ方程式 [F,p]=opt(A,B,C,Q,R) を準備し,例題5.2を解け。 %opt.m ここで,4行目でハミルトン行列の固有値問題を解き,安定固有値の添字を5行目の index に得て,リッカチ方程式の解 X を得ている。 例題5.2を解くには,MATLABにつぎのコマンドを与えればよい。 %lqr.m また, p が閉ループ系の固有値 eig(A-B*F) としてみれば確認できる。 |
演習5.4 演習5.2を,例題5.4にならって,MATLABで解け。
演習5.5 3次系
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \dot{x}_3(t) \end{array}\right] %}_{\dot{x}(t)} = \left[\begin{array}{cccc} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -1 \end{array}\right] %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \\ x_3(t) \end{array}\right] %}_{x(t)} + \left[\begin{array}{cc} 0 & 0 \\ 1 & -1 \\ 0 & 1 \\ \end{array}\right] \left[\begin{array}{c} u_1(t) \\ u_2(t) \end{array}\right] \\ \left[\begin{array}{c} y_1(t) \\ y_2(t) \end{array}\right] = \left[\begin{array}{cccc} 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \\ x_3(t) \end{array}\right] %}_{x(t)} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dae10affe1e50a41b97b2aaeb226a5bd_l3.png)
を安定化する状態フィードバック![]() を,つぎの評価関数を最小にするように求めよ。
を,つぎの評価関数を最小にするように求めよ。
![]()
演習5.6 4次系
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \dot{x}_3(t) \\ \dot{x}_4(t) \end{array}\right] %}_{\dot{x}(t)} = \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -1 & 1 & 0 & 0 \\ 1 & -1 & 0 & 0 \end{array}\right] %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \\ x_3(t) \\ x_4(t) \end{array}\right] %}_{x(t)} + \left[\begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \end{array}\right] u(t) \\ y(t) = \left[\begin{array}{cccc} 0 & 1 & 0 & 0 \end{array}\right] %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \\ x_3(t) \\ x_4(t) \end{array}\right] %}_{x(t)} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4e0489ca273b85f434222050e1404718_l3.png)
を安定化する状態フィードバック![]() を,つぎの評価関数を最小にするように求めよ。
を,つぎの評価関数を最小にするように求めよ。
![]()
5.2 オブザーバベースト・コントローラの最適設計
|
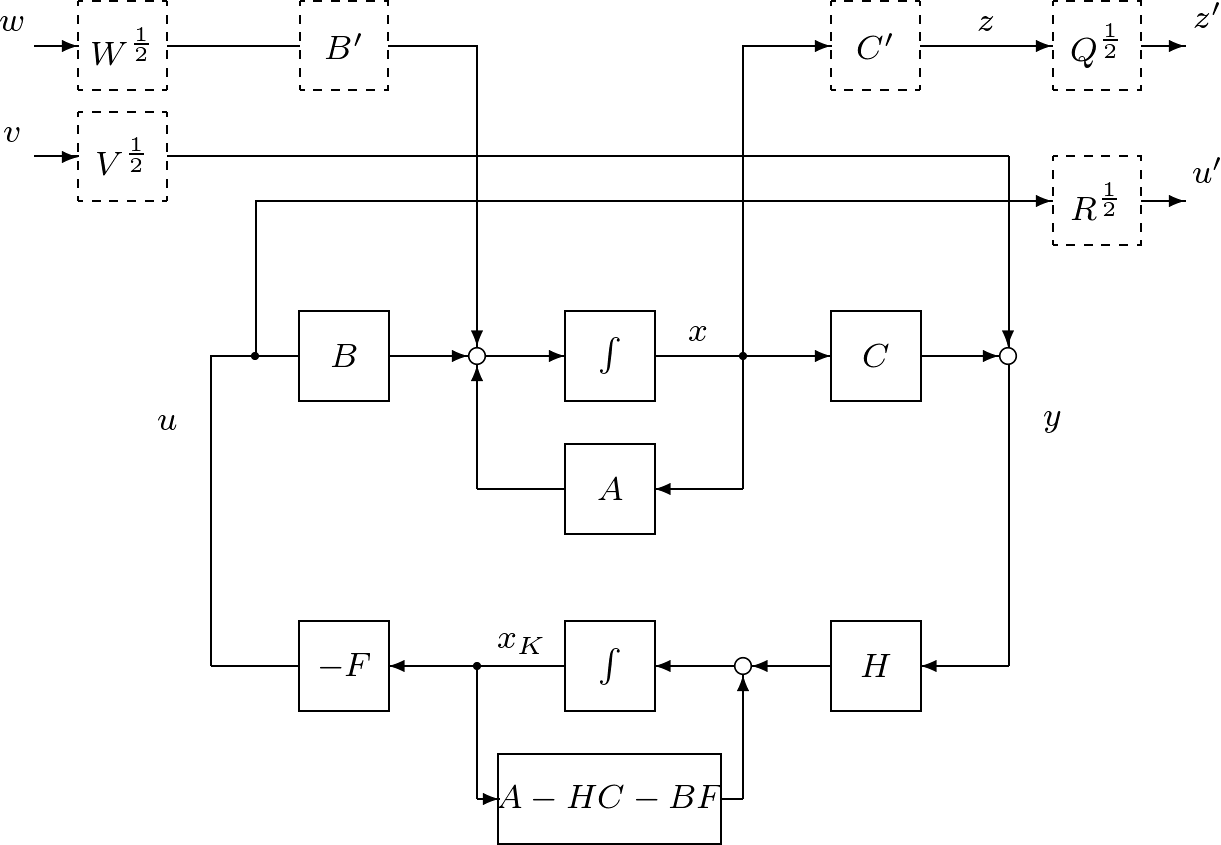
オブザーバベースト・コントローラによる閉ループ系の時間応答に関する評価するために,つぎのブロック線図を考える。
ここで,新しい入力 この
に対して,オブザーバベースト・コントローラ
による閉ループ系は,次式で表される。
このインパルス応答行列
に関する評価規範として
を設定し,これを最小化する問題を解くことができる( Step 1 行列方程式
の解
Step 2 行列方程式
の解
|
|
例題5.5 1次系
において
|
演習5.7 1次系![]() に対するオブザーバベースト・コントローラを,
に対するオブザーバベースト・コントローラを,
例題5.5のCAREにおいて![]() ,
,![]() ,FAREにおいて
,FAREにおいて![]() ,
,![]() と選んで構成せよ。
と選んで構成せよ。
|
例題5.6 LQG制御則を設計するためのMファイルを作成せよ。
[AK,BK,CK,pK,pcare,pfare] = optobc(A,B,C,CC,Q,R,BB,W,V) 解答 例題5.4で作成したMファイル opt.m を用いる。 %optobc.m |
演習5.8 演習5.7を,例題5.6で作成したMファイル optobc.m を用いて解け。
演習問題の解答
【演習5.1】
(1) ![]() ,
,
(2) ![]() ,
,
(3) ![]() 。
。
MATLABによるシミュレーションはつぎのように行えばよい。
%lqr1.m
T=1; K=1; a=-1/T; b=K/T; c=1; t=0:0.1:5; x0=1;
s0=ss(a,b,c,0); y0=initial(s0,x0,t);
f1=-1+sqrt(2); s1=ss(a-b*f1,b,c,0); y1=initial(s1,x0,t); u1=-f1*y1;
f2=-1+sqrt(3); s2=ss(a-b*f2,b,c,0); y2=initial(s2,x0,t); u2=-f2*y2;
f3=-1+sqrt(11); s3=ss(a-b*f3,b,c,0); y3=initial(s3,x0,t); u3=-f3*y3;
figure(1),subplot(121),plot(t,y0,t,y1,t,y2,t,y3),grid,title(‘y’)
figure(1),subplot(122),plot(t,u1,t,u2,t,u3),grid,title(‘u’)
【演習5.2】
(1)リッカチ方程式
![Rendered by QuickLaTeX.com \begin{array}{ll} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & -1 \end{array}\right] + \left[\begin{array}{cc} 0 & 0 \\ 1 & -1 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]- \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \\ \times \left[\begin{array}{c} 0 \\ 1 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] \left[\begin{array}{cc} 1 & 0 \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-77abcc710f7d176292ed41df61fb44dd_l3.png)
を要素ごとに整理して
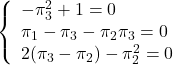
を得る。![]() を満たす解は,
を満たす解は,![]() 。
。
したがって
![]()
%[f,p]=opt([0 1;0 -1],[0;1],[1 0],1,1)
(2)リッカチ方程式
![Rendered by QuickLaTeX.com \begin{array}{ll} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right] + \left[\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]- \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \\ \times \left[\begin{array}{c} 0 \\ 1 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] \left[\begin{array}{cc} 1 & 0 \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3be713e989b828432150c9bf7d0a7fe_l3.png)
を要素ごとに整理して
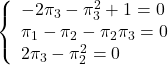
を得る。![]() を満たす解は,
を満たす解は,![]() 。したがって
。したがって
![]()
%[f,p]=opt([0 1;-1 0],[0;1],[1 0],1,1)
【演習5.3】
リッカチ方程式
![Rendered by QuickLaTeX.com \begin{array}{ll} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] + \left[\begin{array}{cc} 0 & -\omega_n^2 \\ 1 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \\ \times \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] q^2 \left[\begin{array}{cc} 1 & 0 \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e4281eae5d3310b57d2a3cdb66eb7865_l3.png)
を要素ごとに整理して
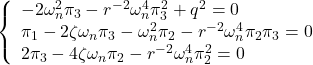
を得る。![]() を満たすものを選ぶと
を満たすものを選ぶと
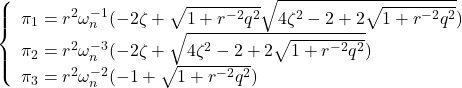
を得る。これらを用いて,![]() と
と![]() の表現式が,例題??と同様にして得られる。
の表現式が,例題??と同様にして得られる。
【演習5.4】
%lqr2.m
A=[0 1;0 -1]; B=[0;1]; C=[1 0]; Q=1; R=1;
[F,p]=opt(A,B,C,Q,R);
sys=ss(A-B*F,B,eye(2,2),0); x0=[1;0];
t=0:0.1:10; x=initial(sys,x0,t)’; y=C*x; u=-F*x;
figure(2),subplot(121),plot(t,y),grid,title(‘y’)
figure(2),subplot(122),plot(t,u),grid,title(‘u’)
(2)の場合,A=[0 1;-1 0] と書き換える。
【演習5.5】
%lqr3.m
A=[0 1 0;0 0 0;0 0 -1]; B=[0 0;1 -1;0 1]; C=[1 0 0;0 0 1];
[F,p]=opt(A,B,C,1,1)
【演習5.6】
%lqr4.m
A=[0 0 1 0;0 0 0 1;-1 1 0 0;1 -1 0 0]; B=[0;0;1;0]; C=[0 1 0 0];
[F,p]=opt(A,B,C,1,1)
【演習5.7】
CARE:![]() に,
に,![]() ,
,![]() ,
,![]() ,
,![]() を代入して,
を代入して,![]() 。
。![]() より
より![]() 。
。
したがって,状態フィードバックゲインは,![]() 。
。
FARE:![]() に,
に,![]() ,
,![]() ,
,![]() ,
,![]() を代入して,
を代入して,![]() 。
。![]() より,
より,![]() 。
。
したがって,オブザーバゲインは,![]() 。
。
以上から,オブザーバベースト・コントローラが,つぎのように得られる。
![]()
【演習5.8】
%lqr5.m
[A
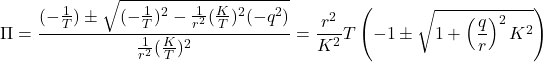
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{l} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] + \left[\begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ 1 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] + \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]\\ = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c0fe9f8513553f489bdfd16b398f4af9_l3.png)
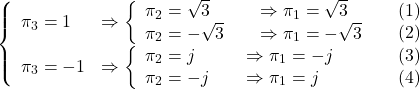
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] %}_{\dot{x}(t)} = %\underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -2\zeta\omega_n \end{array}\right] %}_{A} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + %\underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] %}_{B} \\ y(t)= %\underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] %}_{C} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1fce5372a6e13e3b5578a08abeba594c_l3.png)
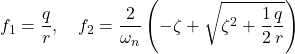
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{l} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & -2\zeta\omega_n \end{array}\right] + \left[\begin{array}{cc} 0 & 0 \\ 1 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] q^{2} \left[\begin{array}{cc} 1 & 0 \end{array}\right]\\ % \left[\begin{array}{cc} % q_1^2 & 0 \\ % 0 & q_2^2 % \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-276692b36c29cb26f7eb5ce869645673_l3.png)
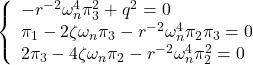
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{l} \left[\begin{array}{cc} f_1 & f_2 \end{array}\right]=r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]=r^{-2}\omega_n^2 \left[\begin{array}{cc} \pi_3 & \pi_2 \end{array}\right]\\ = \left[\begin{array}{cc} \frac{q}{r} & \frac{2}{\omega_n}\left(-\zeta+\sqrt{\zeta^2+\frac{1}{2}\frac{q}{r}}\right) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3d6734e1d1303cee73bacf9ffc4267f_l3.png)
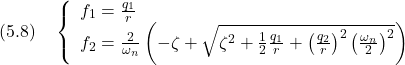
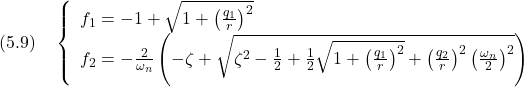
![Rendered by QuickLaTeX.com \displaystyle{(5.10)\quad \underbrace{ \left[\begin{array}{cc} A & -BR^{-1}B^T \\ -C^TQC & -A^T \end{array}\right]}_{M(2n\times 2n)} \underbrace{ \left[\begin{array}{c} V_1 \\ V_2 \end{array}\right]}_{V^-(2n\times n)} = \underbrace{ \left[\begin{array}{c} V_1 \\ V_2 \end{array}\right]}_{V^-(2n\times n)} \underbrace{ {\rm diag}\{\lambda_1,\cdots,\lambda_n\} }_{\Lambda^-(n\times n)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-835801247f79b1b7c7493fad4e900dbd_l3.png)
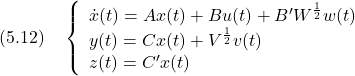
![Rendered by QuickLaTeX.com \displaystyle{(5.14)\quad \left\{\begin{array}{rcl} \left[\begin{array}{cc} \dot{x}(t) \\ \dot{\hat{x}}(t) \end{array}\right]&=& \underbrace{ \left[\begin{array}{cc} A & -BF \\ HC&A-HC-BF \end{array}\right] }_{A_{CL}} \left[\begin{array}{cc} {x}(t) \\ \hat{x}(t) \end{array}\right] \\ &&+ \underbrace{ \left[\begin{array}{cc} B'W^{\frac{1}{2}} & 0 \\ 0 & HV^{\frac{1}{2}} \end{array}\right] }_{B_{CL}} \left[\begin{array}{cc} {w}(t) \\ {v}(t) \end{array}\right] \\ \left[\begin{array}{cc} {z'}(t) \\ {u'}(t) \end{array}\right] &=& \underbrace{ \left[\begin{array}{cc} Q^{\frac{1}{2}}C' & 0 \\ 0 & -R^{\frac{1}{2}}F \end{array}\right] }_{C_{CL}} \left[\begin{array}{cc} {x}(t) \\ \hat{x}(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1b91a2937df2ee79c45fd36c4cd78be7_l3.png)