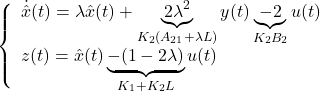|
【本章のねらい】 ・ 状態オブザーバを構成する。 ・ 可観測性と可検出性を判定する。 |
4.1 状態オブザーバ
|
いま制御対象は平衡状態にあるとし,何らかの要因でこれが乱されたとき,速やかに元の平衡状態に戻す手段として,
に対する状態フィードバック
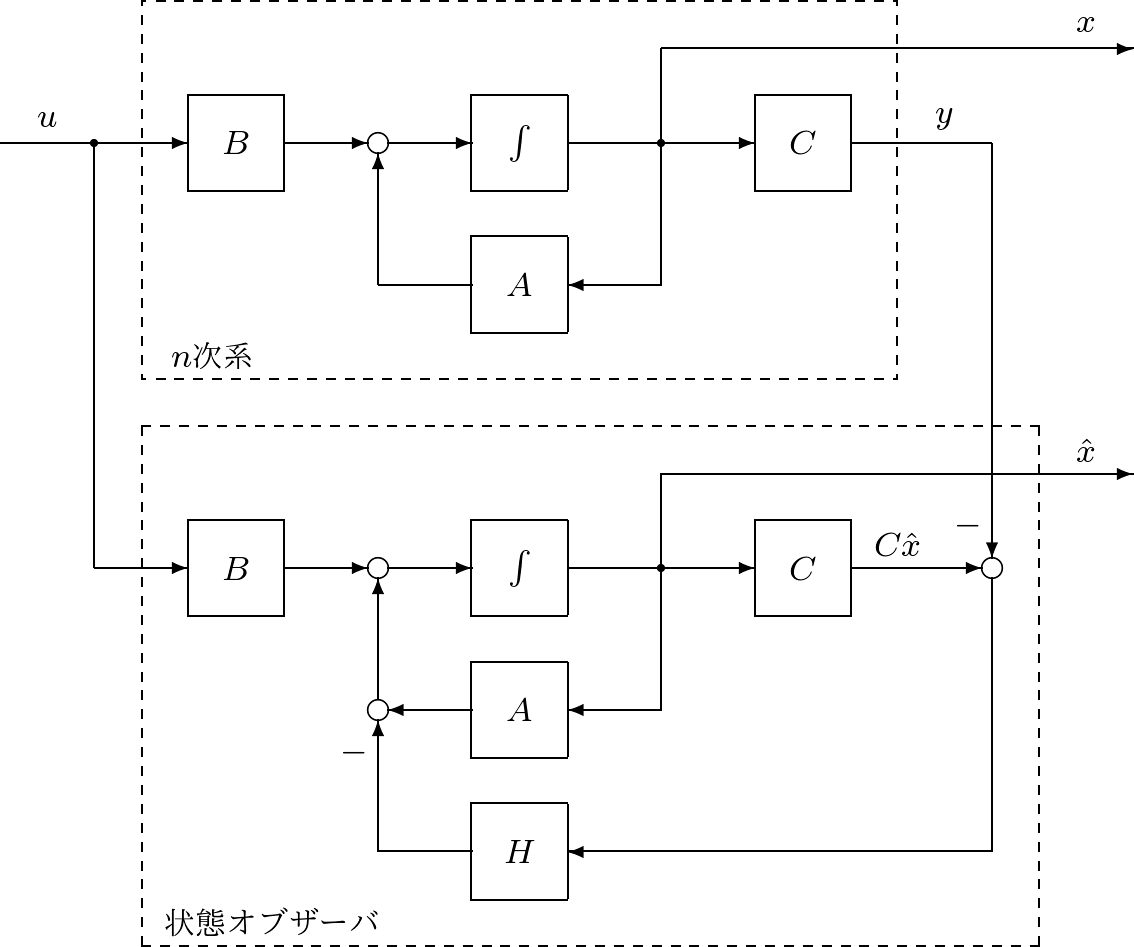
を考えた。しかしながら,現実には状態変数をすべて計測できる場合は少ない。したがって,状態フィードバックは実際には実施できるとは限らない。そこで,状態オブザーバとよばれる
が考案されている。ここで,サイズ
実際,(4.3)から(4.1)の第1式を辺々引き算すると
ここで,行列
となって, 一つのアプローチは,つぎの仮想的な
を安定化する状態フィードバック
を求めることである。実際,閉ループ系は
となって,行列 したがって,前章の状態フィードバックの設計法をそのまま援用できるが,実際には次章のLQG制御問題として解く場合が多い。 例題4.1 2次系
に対する状態オブザーバ
行列
これらから,オブザーバゲイン
したがって,求める状態オブザーバ
演習4.1 2次系
に対する状態オブザーバ 例題4.2 例題4.1において, %obs_err.m 演習4.2 演習4.1において, さて,
のように実施するとき,オブザーバベースト・コントローラは
となる。このとき,閉ループ系はつぎのように表される(
このように閉ループ系の 例題4.3 1次系
に対する状態フィードバック
と,状態オブザーバ
を考える。このときオブザーバベースト・コントローラ
による閉ループ系の
すなわち
で表される。この行列
より, 演習4.2 例題4.3において, |
4.2 可観測性と可検出性
|
どのような 【可検出性の定義とその等価な条件】 定義D0: 状態オブザーバを構成可能 これらの条件の一つが成り立つとき 【可観測性の定義とその等価な条件】 定義O0: 任意有限時間の入力と出力から,初期状態を一意に決定可能 これらの条件の一つが成り立つとき 例題4.4 つぎの
(2) 可観測性行列は, (3) 可観測性行列は, 演習4.4 例題4.4における可観測性の判定を, |
4.3 状態オブザーバの低次元化
| これまで,状態オブザーバの出力
が考案されている。ここで,サイズ
を満足させることができれば
が成り立ち,これから
したがって
を得る(テキスト「線形システム制御入門」の 4.3節参照)。特に, 例題4.5 1入力
に対して,
ここで,
と選べば,次式が成り立つ。
演習4.5 例題4.1の2次系に対する恒等関数オブザーバを,その固有値が 例題4.6 例題4.5の1入力
を推定する線形関数オブザーバの一つは,つぎに
ただし,
と選べば,次式が成り立つ。
演習4.6 例題4.1の2次系に対して,状態フィードバック |
演習問題の解答
| 【演習4.1】 行列
行列
したがって,求める状態オブザーバ
【演習4.2】 %obs_err2.m 【演習4.3】 %observer_based_controller.m 【演習4.4】
したがって,この2次系は可観測である。 (2)
したがって,この2次系は可観測ではない。 (3)
したがって,この2次系は可観測ではない。 【演習4.5】
ただし, %obs_err3.m 【演習4.6】
ただし, %obs_err4.m |
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{cc} 0 \\ 1 \end{array}\right] }_{B} u(t)\\ y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{x(t)} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b4716f40d1006ce97470291edbcab935_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ {\rm det}(\lambda I_2-A)= {\rm det}\left[\begin{array}{cc} \lambda & -1 \\ 0 & \lambda \end{array}\right] =\lambda^2+\underbrace{0}_{a_1}\lambda+\underbrace{0}_{a_2} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4a8163de84bd0261dff1fa933592b34c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{cc} 0 \\ 1 \end{array}\right] }_{B} u(t)\\ y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 1 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{x(t)} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cb616bd20ad3679652dda6f9def23eb8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{x}(t)\\ \dot{\hat{x}}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} a & -bf \\ hc & a-hc-bf \end{array}\right] }_{A_F} \left[\begin{array}{c} {x}(t)\\ {\hat{x}}(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7399b50c26a8ee8f72f43f1c373710a1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{lll} &&{\rm det}(\lambda I_2-A_F) ={\rm det} \left[\begin{array}{cc} \lambda-a & bf \\ -hc & \lambda-a+hc+bf \end{array}\right]\\ &&=(\lambda-a)(\lambda-a+hc+bf)+bfhc\\ &&=\lambda^2-(a-bf+a-hc)\lambda+(a-bf)(a-hc)\\ &&=(\lambda-(a-bf))(\lambda-(a-hc))=0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-773a683e5ed9d01a0b5fb9fed4d9fa15_l3.png)
![Rendered by QuickLaTeX.com {\rm rank}\, \underbrace{ \left[\begin{array}{c} C \\ CA \\ \vdots\\ CA^{n-1} \end{array}\right] }_{observability\ matrix} =n](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6253173de124e69f731cff9f00238073_l3.png)
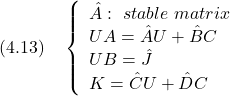
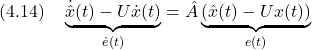
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{y}(t) \\ \ddot{y}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & I_p \\ A_{21} & A_{22} \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} y(t) \\ \dot{y}(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ B_2 \end{array}\right] }_B u(t) \\ y(t)= \underbrace{ \left[\begin{array}{cc} I_p & 0 \end{array}\right] }_C \underbrace{ \left[\begin{array}{c} y(t) \\ \dot{y}(t) \end{array}\right] }_{x(t)} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dd502a7f8d2f5cdb3309be9babf3c735_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \dot{\hat{x}}(t)= \underbrace{(A_{22}-L)}_{\hat{A}}\hat{x}(t) +\underbrace{(A_{21}+(A_{22}-L)L)}_{\hat{B}}y(t) +\underbrace{B_{2}}_{\hat{J}}u(t)\\ z(t)= \underbrace{ \left[\begin{array}{c} 0 \\ I_p \end{array}\right] }_{\hat{C}} \hat{x}(t) + \underbrace{ \left[\begin{array}{c} I_p \\ L \end{array}\right] }_{\hat{D}} y(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d2e714a3407b24c35a02e8bde698f9a0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{cc} A_{21} & A_{22}-L \\ I_p & 0\\ 0 & I_p \end{array}\right] }_{ \left[\begin{array}{cc} UA \\ I_{2p} \end{array}\right]} = \underbrace{ \left[\begin{array}{cc} A_{22}-L & A_{21}+(A_{22}-L)L\\ 0 & I_p\\ I_p & L \end{array}\right] }_{ \left[\begin{array}{cc} \hat{A} & \hat{B} \\ \hat{C} & \hat{D} \end{array}\right]} \underbrace{ \left[\begin{array}{cc} -L & I_p \\ I_p & 0 \end{array}\right] }_{ \left[\begin{array}{cc} U \\ C \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4437dc03385f40f22d80730c9970d4e5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ u(t)= \underbrace{ \left[\begin{array}{cc} K_1 & K_2 \end{array}\right] }_K \underbrace{ \left[\begin{array}{c} y(t) \\ \dot{y}(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-38415ee373992f2396ca53180700b8cb_l3.png)
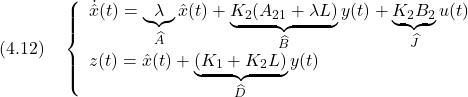
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{cc} K_2A_{21} & K_2(A_{22}-L) \\ K_1 & K_2 \end{array}\right] }_{ \left[\begin{array}{cc} UA \\ K \end{array}\right]} = \underbrace{ \left[\begin{array}{cc} \lambda & K_2(A_{21}+\lambda L) \\ 1 & K_1+K_2L \end{array}\right] }_{ \left[\begin{array}{cc} \hat{A} & \hat{B} \\ \hat{C} & \hat{D} \end{array}\right]} \underbrace{ \left[\begin{array}{cc} -K_2L & K_2 \\ I_p & 0 \end{array}\right] }_{ \left[\begin{array}{cc} U \\ C \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-af379103f3c6d8408714f762d43eaae9_l3.png)
![Rendered by QuickLaTeX.com {\rm det}(\lambda I_2-A)= {\rm det}\left[\begin{array}{cc} \lambda & -1 \\ 0 & \lambda \end{array}\right] =\lambda^2+\underbrace{0}_{a_1}\lambda+\underbrace{0}_{a_2}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-683fa53a06a69cdf8560c0f6dd23d977_l3.png)
![Rendered by QuickLaTeX.com {\rm rank}\, \left[\begin{array}{c} C \\ A-\lambda_i I_2 \end{array}\right]= {\rm rank} \left[\begin{array}{ccc} 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{array}\right]= 2\ \ (i=1,2)](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-30cd66cd7df59213c8b0268c2be8051e_l3.png)
![Rendered by QuickLaTeX.com {\rm rank}\, \left[\begin{array}{c} C \\ A-\lambda_i I_2 \end{array}\right]= {\rm rank} \left[\begin{array}{ccc} 0 & 1 \\ 0 & 1 \\ 0 & 0 \end{array}\right]= 1\ \ (i=1,2)](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3ebec8ef15f1eec0c91cca84d38ca025_l3.png)
![Rendered by QuickLaTeX.com {\rm rank}\, \left[\begin{array}{c} C \\ A-\lambda_1 I_2 \end{array}\right]= {\rm rank} \left[\begin{array}{ccc} 1 & 1 \\ 0 & 1 \\ 0 & -1 \end{array}\right]= 2](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eeba5efd60e4377e2987397eae0f3d4a_l3.png)
![Rendered by QuickLaTeX.com {\rm rank}\, \left[\begin{array}{c} C \\ A-\lambda_2 I_2 \end{array}\right]= {\rm rank} \left[\begin{array}{ccc} 1 & 1 \\ -1 & 1 \\ 0 & 0 \end{array}\right]= 1](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-062a4b6b19aa5147e9e189c402950ecf_l3.png)
![Rendered by QuickLaTeX.com \left\{\begin{array}{l} \dot{\hat{x}}(t)= \underbrace{-L}_{A_{22}-L} \hat{x}(t) \underbrace{-L^2}_{A_{21}+(A_{22}-L)L} y(t)+ \underbrace{1}_{B_{2}} u(t)\\ z(t)= \left[\begin{array}{c} 0 \\ 1 \end{array}\right] \hat{x}(t) + \left[\begin{array}{c} 1 \\ L \end{array}\right] y(t) \end{array}\right.](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d477eebdabe870a1925aa162c9c0ac2f_l3.png)