SMオブザーバベース・追従SMI制御…Homework
[0] まず準備の復習から始めます。
制御対象の状態空間表現として次式を考えます。
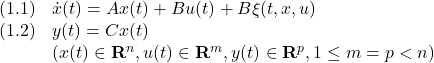
これに対して、積分動作
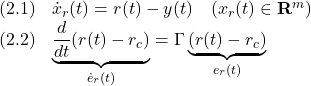
とSM状態オブザーバ
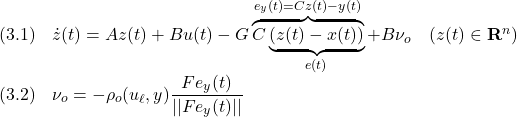
を考えます。
●以下では、![]() の代わりに
の代わりに![]() を用いた制御則
を用いた制御則![]() を
を![]() で表します。
で表します。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \hat{u}(t)=\underbrace{-L\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-L_rr(t)+L_{\dot r}\dot{r}(t)}_{\hat {u}_L}+\hat{\nu}_c\\ \displaystyle{\hat{\nu}_c=L_n\frac{P_2(S\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-S_rr(t))}{||P_2(S\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-S_rr(t))||}}\\ L=(S\tilde{B})^{-1}(S\tilde{A}-\Phi S)\\ L_r=(S\tilde{B})^{-1}(\Phi S_r+S_2MB_r)\\ L_{\dot r}=(S\tilde{B})^{-1}S_r\\ L_n=(S\tilde{B})^{-1}\rho_c(\hat{u}_L,y) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-024f6914b3128301f6c6ae196567ba16_l3.png)
ここでスイッチング関数は、![]() を
を![]() と分割して、次式で表されるとしています。
と分割して、次式で表されるとしています。
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right] %}_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I_m \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right] %}_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-027f6a001ff2fd6efdf5b3456395f8b3_l3.png)
[1] (3.1)から(1.1)を辺々引き算して、誤差方程式
![]()
を得ます。![]() を用いて、(2.1)は
を用いて、(2.1)は
![]()
となります。また(3.1)は、![]() の代わりに
の代わりに![]() を用いることにすれば
を用いることにすれば
![]()
と表せます。
●(7)と(8)をまとめて
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \boxed{\begin{array}{l} \left[\begin{array}{c} \dot x_r(t)\\ \dot z(t) \end{array}\right] = \left[\begin{array}{cc} 0_{m\times m} & -C \\ 0_{n\times m} & A \\ \end{array}\right] \left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right] + \left[\begin{array}{c} I_p\\ -G \end{array}\right] e_y(t)\\ + \left[\begin{array}{c} r(t)\\ B(\hat{u}(t)+\nu_o) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-65eb681dec39ab633fe7a5bbc2b85d2c_l3.png)
ここで座標変換
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]= \underbrace{\left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ S_1 & S_2 \\ \end{array}\right]}_{\bar T} \left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]\\ \Leftrightarrow \left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]= \underbrace{\left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ -M & S_2^{-1} \\ \end{array}\right]}_{\bar{T}^{-1}} \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]\quad(M=S_2^{-1}S_1) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4df32cc888cc01697c0d0a7a4a8de076_l3.png)
を行うと
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \bar{T}^{-1} \left[\begin{array}{c} \dot{\tilde{z}}_1(t)\\ \dot{s}(t) \end{array}\right] = \underbrace{\left[\begin{array}{cc|c} 0_{m\times m} & -C_1 & -C_2 \\ 0_{n-m\times m} & A_{11} & A_{12} \\\hline 0_{m\times m} & A_{21} & A_{22} \end{array}\right]}_{\left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12} \\ \tilde{A}_{21} & \tilde{A}_{22} \end{array}\right]} \left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ -M & S_2^{-1} \\ \end{array}\right] \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{c} I_p\\ -G_1\\\hline -G_2 \end{array}\right] e_y(t) + \left[\begin{array}{c} r(t)\\ 0\\\hline B_2(\hat{u}(t)+\nu_o) \end{array}\right]\\ = \underbrace{\left[\begin{array}{cc} \tilde{A}_{11}-\tilde{A}_{12}M & \tilde{A}_{12}S_2^{-1}\\ \tilde{A}_{21}-\tilde{A}_{22}M & \tilde{A}_{22}S_2^{-1} \end{array}\right]}_{\tilde{A}\bar{T}^{-1}} \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right] - \left[\begin{array}{c} \bar{G}_1\\ G_2 \end{array}\right] e_y(t)\\ + \left[\begin{array}{c} B_rr(t)\\ B_2(\hat{u}(t)+\nu_o) \end{array}\right]\\ (\left[\begin{array}{c} G_1\\ G_2 \end{array}\right] =\left[\begin{array}{c} A_{12}C_2^{-1} \\ A_{22}C_2^{-1}-C_2^{-1}A_{22}^S \end{array}\right], \quad\bar{G}_1= \left[\begin{array}{c} -I_p\\ G_1 \end{array}\right]) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-da08553d36abc2e12fd0c39618cc6763_l3.png)
したがって
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \left[\begin{array}{c} \dot{\tilde{z}}_1(t)\\ \dot{s}(t) \end{array}\right] = \underbrace{\left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ S_1 & S_2 \\ \end{array}\right] \left[\begin{array}{cc} \tilde{A}_{11}-\tilde{A}_{12}M & \tilde{A}_{12}S_2^{-1}\\ \tilde{A}_{21}-\tilde{A}_{22}M & \tilde{A}_{22}S_2^{-1} \end{array}\right]}_{\bar{T}\tilde{A}\bar{T}^{-1}} \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]\\ - \left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ S_1 & S_2 \\ \end{array}\right] \left[\begin{array}{c} \bar{G}_1\\ G_2 \end{array}\right] e_y(t) + \left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ S_1 & S_2 \\ \end{array}\right] \left[\begin{array}{c} B_rr(t)\\ B_2(\hat{u}(t)+\nu_o) \end{array}\right]\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1da3c1791a8da84361163ffde267324f_l3.png)
すなわち、第1ブロック行は
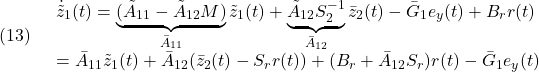
第2ブロック行は(5)を用いて、![]() とおいて
とおいて
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{l} \dot{s}(t)= \underbrace{((S_1\bar{A}_{11}+S_2(\tilde{A}_{21}-\tilde{A}_{22}M))\tilde{z}_1(t)+(S_1\bar{A}_{12}+S_2\tilde{A}_{22}S_2^{-1})s(t)}_{S\tilde{A}\bar{T}^{-1}\left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]=S\tilde{A}\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]}\\ -\underbrace{(S_1\bar{G}_1+S_2G_2)}_{\bar G_2}e_y(t)+S_1B_rr(t)\\ +\underbrace{S_2B_2}_{\Lambda}(L\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]+L_rr(t)+S_r\dot{r}(t)+\hat{\nu}_c+\nu_o)\\ =S\tilde{A}\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]-\bar{G}_2e_y(t)+S_1B_rr(t)\\ +\Lambda(-\Lambda^{-1}(S\tilde{A}-\Phi S)\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]-\Lambda^{-1}(\Phi S_r+S_2MB_r)r(t)+\Lambda^{-1}S_r\dot{r}(t))\\ +\Lambda(\hat{\nu}_c+\nu_o)\\ =S\tilde{A}\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]-\bar{G}_2e_y(t)+S_1B_rr(t)\\ -(S\tilde{A}-\Phi S)\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]-(\Phi S_r+S_2MB_r)r(t)+S_r\dot{r}(t)+\Lambda(\hat{\nu}_c+\nu_o)\\ =\Phi (\underbrace{S\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]}_{s(t)}-S_rr(t))+S_r\dot{r}(t)-\bar{G}_2e_y(t)+\Lambda(\hat{\nu}_c+\nu_o) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ebec66163067a3490f53ebceab553d5e_l3.png)
(13)と(14)の結果は、次のようにまとめられます。
![]()
ここで
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \begin{array}{l} \underbrace{\left[\begin{array}{c} \zeta_1(t)\\ \zeta_2(t) \end{array}\right]}_{\zeta(t)}= \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]+ \left[\begin{array}{c} \bar{A}_{11}^{-1}(\bar{A}_{12}S_r+B_r)r_c\\ -S_rr(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c676bab7a7f2b7c956feb633f175faa2_l3.png)
を定義すると
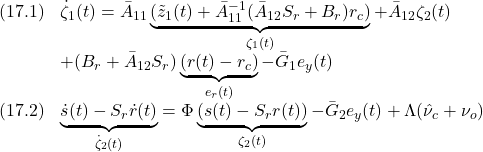
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} \underbrace{\left[\begin{array}{c} \dot \zeta_1(t)\\ \dot \zeta_2(t) \end{array}\right]}_{\dot{\zeta}(t)}= \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]}_{A_c} \underbrace{\left[\begin{array}{c} \zeta_1(t)\\ \zeta_2(t) \end{array}\right]}_{\zeta(t)}\\ - \underbrace{\left[\begin{array}{c} \bar{G}_1\\ \bar{G}_2 \end{array}\right]}_{\bar{G}} \underbrace{e_y(t)}_{Ce(t)} + \underbrace{\left[\begin{array}{c} B_r+\bar{A}_{12}S_r\\ 0 \end{array}\right]}_{\bar{G}_r}e_r(t) + \underbrace{\left[\begin{array}{c} 0\\ \Lambda \end{array}\right]}_{\bar\Lambda}(\hat{\nu}_c+\nu_o) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e698246bb04c91be373318b20c960104_l3.png)
を得ます。これを誤差方程式(6)すなわち
![]()
と合わせて、閉ループ系は次式で表されます。
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad \begin{array}{l} \left[\begin{array}{c} \dot{e}(t)\\ \dot \zeta(t) \end{array}\right]= \underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]}_{A_G} \left[\begin{array}{c} e(t)\\ \zeta(t) \end{array}\right]\\ + \left[\begin{array}{c} 0\\ \bar{G}_r \end{array}\right]e_r(t) + \left[\begin{array}{c} B\\ \bar\Lambda \end{array}\right]\nu_o + \left[\begin{array}{c} 0\\ \bar\Lambda \end{array}\right]\hat{\nu}_c - \left[\begin{array}{c} B\\ 0 \end{array}\right]\xi(t,x,\hat{u}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8e6c6626c17ebcf75a8e1b658d9e4738_l3.png)
ここまでの手順を、関数ob_smiとしてプログラムすることにします。
●以上に基づく設計手順を、数値例で示します。
| MATLAB |
|

図1 SMオブザーバベースSMI追従制御系のシミュレーション例
Note C92 閉ループ系の安定性
●閉ループ系は(19)と(3.2)を合わせて
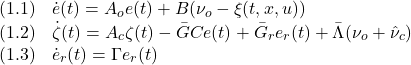
で表されます。これに対して次のリャプノフ関数を考えます。
![]()
ここで、正定行列![]() 、
、![]() 、
、![]() は、それぞれ安定行列
は、それぞれ安定行列![]() 、
、![]() 、
、![]() のリャプノフ行列とし、次のリャプノフ方程式の解とします。
のリャプノフ行列とし、次のリャプノフ方程式の解とします。
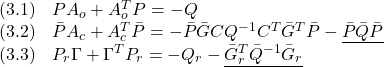
●![]() は、リャプノフ方程式
は、リャプノフ方程式
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P} \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]}_{A_c} +\underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]^T}_{A_c^T} \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P}<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9f1e612deced36f7c7db9b14fc59dc21_l3.png)
を満足するブロック対角行列とします。ここで、正定行列![]() 、
、![]() は、それぞれ安定行列
は、それぞれ安定行列![]() 、
、![]() に対する次のリャプノフ不等式の解です。
に対する次のリャプノフ不等式の解です。
![]()
![]()
このとき、![]() と
と![]() は、次のリャプノフ不等式の解を構成するとします。
は、次のリャプノフ不等式の解を構成するとします。
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{\left[\begin{array}{cc} P & 0\\ 0 & \bar{P} \end{array}\right]}_{P_G} \underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]}_{A_G} +\underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]^T}_{A_G^T} \underbrace{\left[\begin{array}{cc} P & 0\\ 0 & \bar{P} \end{array}\right]}_{P_G}<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dceeb6208f924a3f6efeaa77bb099a32_l3.png)
これは次式と等価です。
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} PA_o & 0\\ -\bar{P}\bar{G}C & \bar{P}A_c \end{array}\right]}_{P_GA_G}+ \underbrace{\left[\begin{array}{cc} PA_o & 0\\ -\bar{P}\bar{G}C & \bar{P}A_c \end{array}\right]^T}_{(P_GA_G)^T} =\left[\begin{array}{cc} -Q & -C^T\bar{G}^T\bar{P}\\ -\bar{P}\bar{G}C & \bar{P}A_c+A_c^T\bar{P} \end{array}\right]<0\\ \Leftrightarrow \bar{P}A_c+A_c^T\bar{P}+\bar{P}\bar{G}CQ^{-1}C^T\bar{G}^T\bar{P}<0\\ \Leftrightarrow A_c\bar{P}^{-1}+\bar{P}^{-1}A_c^T+\bar{G}CQ^{-1}C^T\bar{G}^T<0\\ \Leftrightarrow A_c\bar{P}^{-1}+\bar{P}^{-1}A_c^T+\bar{G}CQ^{-1}C^T\bar{G}^T=-\bar{Q}\quad(\bar{Q}>0) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c62b77d490c2fb89c0065a176246cf86_l3.png)
ここで、新しいパラメータ![]() を導入し、次の公式を用いています。
を導入し、次の公式を用いています。
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]<0\\ &\Leftrightarrow& P-MQ^{-1}M^T<0,\ Q<0\\ &\Leftrightarrow& P<0,\ Q-M^TP^{-1}M<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eee622434bc9e2fc505eb899dbb107cb_l3.png) |
いま適当な![]() と
と![]() を与えて、
を与えて、
![]()
![]()
を解いて、![]() と
と![]() を定めるものとします。このとき(7)は
を定めるものとします。このとき(7)は
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]}_{A_c} \underbrace{\left[\begin{array}{cc} \bar{P}_1^{-1} & 0\\ 0 & \bar{P}_2^{-1} \end{array}\right]}_{\bar{P}^{-1}} + \underbrace{\left[\begin{array}{cc} \bar{P}_1^{-1} & 0\\ 0 & \bar{P}_2^{-1} \end{array}\right]}_{\bar{P}^{-1}} \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]^T}_{A_c^T}\\ +\underbrace{\left[\begin{array}{c} \bar{G}_1\\ \bar{G}_2 \end{array}\right]}_{\bar{G}} \underbrace{CQ^{-1}C^T}_{Q_{22}} \underbrace{\left[\begin{array}{c} \bar{G}_1\\ \bar{G}_2 \end{array}\right]^T}_{\bar{G}^T}\\ = \underbrace{\left[\begin{array}{cc} \bar{A}_{11}\bar{P}_1^{-1} & \bar{A}_{12}\bar{P}_2^{-1}\\ 0 & \Phi \bar{P}_2^{-1} \end{array}\right]}_{A_c\bar{P}^{-1}} + \underbrace{\left[\begin{array}{cc} \bar{A}_{11}\bar{P}_1^{-1} & \bar{A}_{12}\bar{P}_2^{-1}\\ 0 & \Phi \bar{P}_2^{-1} \end{array}\right]^T}_{(A_c\bar{P}^{-1})^T}\\ +\underbrace{\left[\begin{array}{cc} \bar{G}_1Q_{22}\bar{G}_1^T &\bar{G}_1Q_{22}\bar{G}_2^T\\ \bar{G}_2Q_{22}\bar{G}_1^T &\bar{G}_2Q_{22}\bar{G}_2^T \end{array}\right]}_{\bar{G}CQ^{-1}C^T\bar{G}^T}\\ = \left[\begin{array}{cc} \bar{A}_{11}\bar{P}_1^{-1}+\bar{P}_1^{-1}\bar{A}_{11}^T+\bar{G}_1Q_{22}\bar{G}_1^T & \bar{A}_{12}\bar{P}_2^{-1}+\bar{G}_1Q_{22}\bar{G}_2^T\\ \bar{P}_2^{-1}\bar{A}_{12}^T+\bar{G}_2Q_{22}\bar{G}_1^T & \Phi\bar{P}_2^{-1}+\bar{P}_2^{-1}\Phi^T+\bar{G}_2Q_{22}\bar{G}_2^T \end{array}\right]\\ = \left[\begin{array}{cc} -\hat{Q}_1+\bar{G}_1Q_{22}\bar{G}_1^T & \bar{A}_{12}\bar{P}_2^{-1}+\bar{G}_1Q_{22}\bar{G}_2^T\\ \bar{P}_2^{-1}\bar{A}_{12}^T+\bar{G}_2Q_{22}\bar{G}_1^T & -\hat{Q}_2+\bar{G}_2Q_{22}\bar{G}_2^T \end{array}\right]<0\\ \Leftrightarrow \left\{\begin{array}{l} \bar{G}_1Q_{22}\bar{G}_1^T +(\bar{A}_{12}\bar{P}_2^{-1}+\bar{G}_1Q_{22}\bar{G}_2^T)\\ \times(\bar{G}_2Q_{22}\bar{G}_2^T -\hat{Q}_2)^{-1}(\bar{P}_2^{-1}\bar{A}_{12}^T+\bar{G}_2Q_{22}\bar{G}_1^T) <\hat{Q}_1\\ \bar{G}_2Q_{22}\bar{G}_2^T <\hat{Q}_2 \end{array}\right. \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d2a4be3ea4336e3bad8a74302a1a87d8_l3.png)
となります。したがって、この制約を(8)の![]() 、(9)の
、(9)の![]() に付けておきます。
に付けておきます。
●以上の準備の下で次式が示され、閉ループ系のリャプノフ安定性が成り立ちます。

ここで、次の平方完成を行っています。
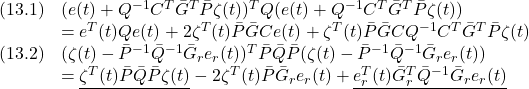
また、次が成り立つことを用いています。
![]()
まず、(14.1)は
![]()
を変形して得られる
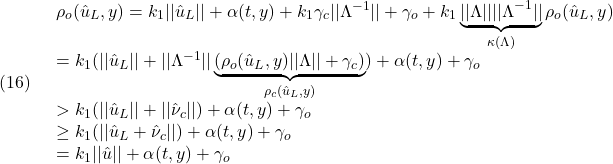
を用いて
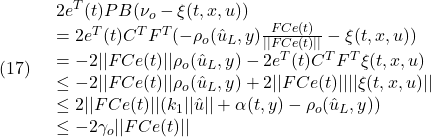
次に、(14.2)は
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} 2\zeta^T(t)\bar{P}\bar{\Lambda}(\nu_o+\hat{\nu}_c)\\ =2\underbrace{\left[\begin{array}{c} \zeta_1(t)\\ \zeta_2(t) \end{array}\right]^T}_{\zeta^T(t)} \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P} \underbrace{\left[\begin{array}{c} 0\\ \Lambda \end{array}\right]}_{\bar\Lambda}(\nu_o+\hat{\nu}_c)\\ =-2\zeta_2^T(t)\bar{P}_2\Lambda\rho_o(\hat{u}_L,y)\frac{FCe(t)}{||FCe(t)||}-2\zeta_2^T(t)\bar{P}_2\Lambda\rho_c(\hat{u}_L,y)\Lambda^{-1} \frac{\bar{P}_2\zeta_2(t)}{||\bar{P}_2\zeta_2(t)||}\\ \le 2||\bar{P}_2\zeta_2(t)||||\Lambda||\rho_o(\hat{u}_L,y)-2\rho_c(\hat{u}_L,y)||\bar{P}_2\zeta_2(t)||\\ =2||\bar{P}_2\zeta_2(t)||(\rho_o(\hat{u}_L,y)||\Lambda||-\rho_c(\hat{u}_L,y))\\ =2||\bar{P}_2\zeta_2(t)||(\rho_c(\hat{u}_L,y)-\gamma_c-\rho_c(\hat{u}_L,y))\\ =-2\gamma_c||\bar{P}_2\zeta_2(t)|| \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-79955beab6ef0705346e5157fe6ced17_l3.png)
Note C92-2 スライディングモードの検討
このSM制御系では、超平面
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad {\cal S}_c=\left\{\left[\begin{array}{c} e\\ \zeta_1\\ \zeta_2 \end{array}\right]\in{\bf R}^{2n+p}: \left\{\begin{array}{l} e_y(t)=Ce(t)=Cz(t)-y(t)=0\\ \zeta_2(t)=s(t)-S_rr(t)=0 \end{array}\right. \right\} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-198a3c5b246cf20144027bbb223bb2b6_l3.png)
においてスライディングモードが生じることを示します。そのために
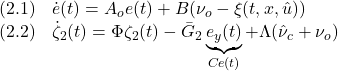
に対して次のリャプノフ関数を考えます。
![]()
この時間微分は次のように計算できます。
![]()
(4)の第1項は、![]() より
より
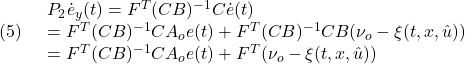
また、(14.1)は![]() を適用して
を適用して
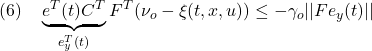
したがって
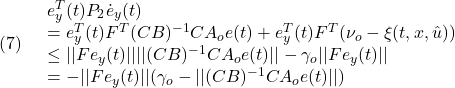
(4)の第2項は、
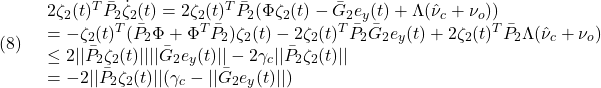
したがって
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \Omega_\eta=\left\{\left[\begin{array}{c} e\\ \zeta_1\\ \zeta_2 \end{array}\right]\in{\bf R}^{2n+p}: \left\{\begin{array}{l} ||(CB)^{-1}CA_oe(t)||<\gamma_o-\eta\\ ||\bar{G}_2e_y(t)||<\gamma_c-\eta \end{array}\right. \right\} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ba3afedc3c9f5d435d671a0460dfdda4_l3.png)
においては
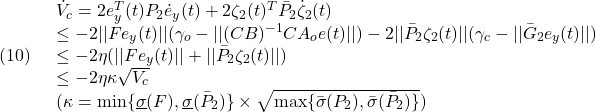
が成り立ち、これより有限時間で![]() となり、超平面
となり、超平面![]() に突入することが分かります(
に突入することが分かります(![]() の表現式はEdwards and Spurgeonによるものです)。
の表現式はEdwards and Spurgeonによるものです)。