出力数>入力数の場合…Homework
[0] 制御対象の状態空間表現として次式を考えます。
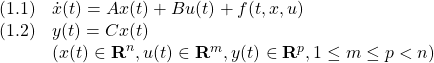
ただし、![]() はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
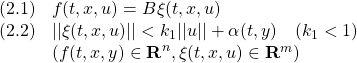
これに対し、次のスイッチング関数を定義します。
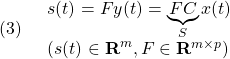
[1] 行列![]() を
を![]() の形にするために、座標変換
の形にするために、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} = \underbrace{ \left[\begin{array}{cc} N_c^T \\ C \\ \end{array}\right] }_{T_c} x(t) \Leftrightarrow x(t)= \underbrace{ \left[\begin{array}{cc} N_c^T \\ C \\ \end{array}\right]^{-1} }_{T_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ece730e4769618b1a1b4da039d7b9673_l3.png)
を行うと(![]() は
は![]() を正則とする適当な行列)、次式を得ます。
を正則とする適当な行列)、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(5.1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} A_{c11} & A_{c12} \\ A_{c21} & A_{c22} \\ \end{array}\right] }_{T_cAT_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} + \underbrace{ \left[\begin{array}{c} B_{c1}\\ B_{c2} \end{array}\right] }_{T_cB} \underbrace{(u(t)+\xi(t,x,u))}_{u'(t)}\\ (B_{c2}\in{\rm\bf R}^{p\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-82e2bbb3826132d675e28645b6cdaee1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5.2)\quad y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] }_{CT_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a7a9e6b215ba844d91319c8cb51519fd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5.3)\quad s(t)= \underbrace{ \left[\begin{array}{cc} 0_{m\times n-p} & F \\ \end{array}\right] }_{FCT_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-81ca3ce18892566a004196f3e47aebc4_l3.png)
●![]() を
を
![]()
のように変換する直交行列![]() を用いて(
を用いて(![]() は正則行列)、座標変換
は正則行列)、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-p} & -B_{c1}(B_{c2}^TB_{c2})^{-1}B_{c2}^T \\ 0_{p\times n-p} & T^T \end{array}\right] }_{T_b} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)}= \underbrace{ \left[\begin{array}{cc} I_{n-p} & B_{c1}(B_{c2}^TB_{c2})^{-1}B_{c2}^T \\ 0_{p\times n-p} & T \end{array}\right] }_{T_b^{-1}} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)}\\ (x''_1(t)\in{\rm\bf R}^{n-p},x''_2(t)\in{\rm\bf R}^{p},T\in{\rm\bf R}^{p\times p}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f1c87f8de33e3f31e6f9bffbf4539320_l3.png)
を行うと、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(8.1)\quad \underbrace{ \left[\begin{array}{c} \dot x''_1(t)\\ \dot x''_2(t) \end{array}\right] }_{\dot{x}''(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \end{array}\right] }_{(T_bT_c)A(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)} + \underbrace{ \left[\begin{array}{c} 0_{n-p\times m}\\ B_2 \end{array}\right] }_ {(T_bT_c)B} u'(t)\\ }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fd900c29bf5651b6ba66e54daeac82a4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.2)\quad y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fb92fb33c1ef65dd6f2d56305d8605c5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.3)\quad \begin{array}{l} s(t)= \underbrace{ \left[\begin{array}{cc} 0_{m\times n-p} & FT \\ \end{array}\right] }_{FC(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)} = \underbrace{ \left[\begin{array}{cc|c} 0_{m\times n-p} & F_1 & F_2 \\ \end{array}\right] }_{FC(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)}\\ (FT=\left[\begin{array}{cc} F_1 & F_2 \end{array}\right], F_1\in{\rm\bf R}^{m\times p-m}, F_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-30c6c57fc79840cb7ba8a7963f16d627_l3.png)
ここで、等価制御が存在する条件![]() は
は
![]()
となります。以下では![]() を仮定します。このとき
を仮定します。このとき![]() の正則性から、正方行列
の正則性から、正方行列![]() も正則となります。
も正則となります。
[2] (7)では、![]() を
を![]() と
と![]() に分割していますが、(8.1)と(8.3)に対するSM標準形を得るために、
に分割していますが、(8.1)と(8.3)に対するSM標準形を得るために、![]() を
を![]() と
と![]() に分割し直して、座標変換
に分割し直して、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \tilde{x}''_1(t)\\ s(t) \end{array}\right] }_{\tilde{x}''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ F_1C' & F_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} \tilde{x}''_1(t)\\ \tilde{x}''_2(t) \end{array}\right] }_{x''(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} \tilde{x}''_1(t)\\ \tilde{x}''_2(t) \end{array}\right] }_{x''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -F_2^{-1}F_1C' & F_2^{-1} \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} \tilde{x}''_1(t)\\ s(t) \end{array}\right] }_{\tilde{x}''(t)}\\ (C'=\left[\begin{array}{cc} 0_{p-m\times n-p} & I_{p-m} \end{array}\right]) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-28d720f19c00491b7c997c513bad202b_l3.png)
を行うと、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \underbrace{ \left[\begin{array}{c} \dot{\tilde{x}}''_1(t)\\ \dot{s}(t) \end{array}\right] }_{\dot{\tilde{x}}''(t)} = \underbrace{ \left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12} \\ \tilde{A}_{21} & \tilde{A}_{22} \end{array}\right] }_{\tilde{A}=(T_sT_bT_c)A(T_sT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} \tilde{x}''_1(t)\\ s(t) \end{array}\right] }_{\tilde{x}''(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \tilde{B}_2 \end{array}\right] }_{\tilde{B}=T_sT_bT_cB} u'(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-53712b6be774e1fea90c24f848d74bac_l3.png)
ただし
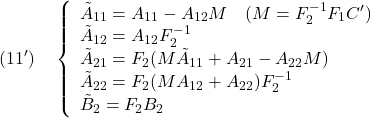
ここで、![]() を安定行列とすることができるかが問題となります。
を安定行列とすることができるかが問題となります。![]() は
は
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \boxed{\tilde{A}_{11}=\underbrace{A_{11}}_{A'}-\underbrace{A_{12}}_{B'} \underbrace{F_2^{-1}F_1}_{K} \underbrace{\left[\begin{array}{cc} 0_{p-m\times n-p} & I_{p-m} \end{array}\right]}_{C'}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-507598a1b9847b9116034c01e1dba046_l3.png)
と書けるので、仮想システム
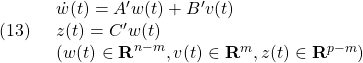
を出力フィードバック
![]()
によって安定化する問題となります。そのためには(13)が可制御かつ可観測で、Kimura-Davisonの条件が成り立つことが必要です。
●(13)の可制御性については
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} {\rm rank} \left[\begin{array}{cc} sI-A & B \end{array}\right]& ={\rm rank} \left[\begin{array}{cc} sI-(T_bT_c)A(T_bT_c)^{-1} & (T_bT_c)B \end{array}\right]\\ ={\rm rank} \left[\begin{array}{ccc} sI-A_{11} & -A_{12} & 0\\ -A_{21} & sI-A_{22} & B_2 \end{array}\right]\\ ={\rm rank} \left[\begin{array}{cc} sI-A_{11} & -A_{12} \end{array}\right]+m\\ ={\rm rank} \left[\begin{array}{cc} sI-A' & B' \end{array}\right]+m \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f0050e4228d42171173c44e1ab9f4b5b_l3.png)
より、(1.1)が可制御であれば(13)も可制御となります。
●(13)の可観測性については、次式に基づいて検討します。
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \begin{array}{l} {\rm rank} \left[\begin{array}{c} sI-A' \\ C' \end{array}\right]\\ ={\rm rank} \left[\begin{array}{cc} sI-A_{1111} & -A_{1112} \\ -A_{1121} & sI-A_{1122} \\ 0 & I_{p-m} \end{array}\right]\ (A'=A_{11}= \left[\begin{array}{cc} A_{1111} & A_{1112} \\ A_{1121} & A_{1122} \end{array}\right])\\ ={\rm rank} \left[\begin{array}{c} sI-A_{1111} \\ A_{1121} \end{array}\right]+p-m\\ ={\rm rank} \left[\begin{array}{c} sI-T_{obs}A_{1111}T_{obs}^{-1} \\ A_{1121} T_{obs}^{-1} \end{array}\right]+p-m\\ (T_{obs}A_{1111}T_{obs}^{-1}= \left[\begin{array}{cc} A_{11}^o & A_{12}^o \\ 0_{n-p-r\times r} & A_{22}^o \end{array}\right], A_{1121} T_{obs}^{-1}= \left[\begin{array}{cc} 0_{p-m\times r} & A_{21}^o \end{array}\right] )\\ ={\rm rank} \left[\begin{array}{cc} sI-A_{11}^o & -A_{12}^o \\ 0_{n-p-r\times r} & sI-A_{22}^o\\ 0_{p-m\times r} & A_{21}^o \end{array}\right]+p-m\\ ={\rm rank}(sI-A_{11}^o)+ \underbrace{{\rm rank}\left[\begin{array}{cc} sI-A_{22}^o\\ A_{21}^o \end{array}\right]}_{n-p-r}+p-m \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-678a84f544a8ee5f97c48b3ee005d9e0_l3.png)
ここで、![]() は、可観測標準形への変換行列です。このとき適当な
は、可観測標準形への変換行列です。このとき適当な![]() に対して最終式の第2項が成り立ちます。したがって、一般には(13)の可観測性は成り立つとは言えないのですが、要は
に対して最終式の第2項が成り立ちます。したがって、一般には(13)の可観測性は成り立つとは言えないのですが、要は![]() を安定行列とできればよいので、この観点から調べていきます。
を安定行列とできればよいので、この観点から調べていきます。
[3] 上の![]() を用いて、(8.1)に対して、座標変換
を用いて、(8.1)に対して、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)} = \underbrace{ \left[\begin{array}{cc|c} T_{obs} & 0 & 0\\ 0 & I_{p-m} & 0 \\\hline 0 & 0 & I_m \end{array}\right] }_{T_a} \underbrace{ \left[\begin{array}{c} {x}''_1(t)\\ {x}''_2(t) \end{array}\right] }_{x''(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} {x}''_1(t)\\ {x}''_2(t) \end{array}\right] }_{x''(t)}= \underbrace{ \left[\begin{array}{cc|c} T_{obs}^{-1} & 0 & 0\\ 0 & I_{p-m} & 0 \\\hline 0 & 0 & I_m \end{array}\right] }_{T_a^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)}\\ (x'''_1(t)\in{\rm\bf R}^{n-m},x'''_2(t)\in{\rm\bf R}^{m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a761762bcf2a930d49f44e4cde5722c7_l3.png)
を行うと、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(18.1)\quad \boxed{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_1(t)\\ \dot x'''_2(t) \end{array}\right] }_{\dot{x}'''(t)} = \underbrace{ \left[\begin{array}{ccc|c} A_{11}^o & A_{12}^o & A_{121}^m & A_{121}\\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221}\\ 0_{p-m\times r} & A_{21}^o & A_{22}^m & A_{1222}\\\hline A_{2120} & A_{2121} & A_{2122} & A_{22} \end{array}\right] }_{(T_aT_bT_c)A(T_aT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)}\\ + \underbrace{ \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline B_2 \end{array}\right] }_ {(T_aT_bT_c)B} u(t)\\ (A_{11}^o\in{\rm\bf R}^{r\times r},A_{22}^o\in{\rm\bf R}^{n-p-r\times n-p-r},A_{22}^m\in{\rm\bf R}^{p-m\times p-m}) \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2f4457165fe43f529be7658c079b9eff_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18.2)\quad \boxed{\begin{array}{l} y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{cc|c} T_{obs}^{-1} & 0 & 0\\ 0 & I_{p-m} & 0 \\\hline 0 & 0 & I_m \end{array}\right] }_{T_a^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)}\\ = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_aT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-05f9d91daa89c529f7c3464c13c2fd69_l3.png)
また、(12)より
![Rendered by QuickLaTeX.com \displaystyle{(12')\quad \begin{array}{l} T_{a'}\tilde{A}_{11}T_{a'}^{-1}=T_{a'}(A'-B'KC')T_{a'}^{-1} \quad (T_{a'}= \left[\begin{array}{cc} T_{obs} & 0 \\ 0 & I_{p-m} \end{array}\right])\\ =T_{a'}A_{11}T_{a'}^{-1}-T_{a'}A_{12} K \left[\begin{array}{ccc} 0_{p-m\times r} & 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]T_{a'}^{-1}\\ = \underbrace{ \left[\begin{array}{c|cc} A_{11}^o & A_{12}^o & A_{121}^m \\\hline 0_{n-p-r\times r} & A_{22}^o & A_{122}^m \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m \end{array}\right]}_{T_{a'}A_{11}T_{a'}^{-1}} -\underbrace{\left[\begin{array}{ccc} A_{121}\\\hline A_{1221}\\ A_{1222} \end{array}\right]}_{T_{a'}A_{12}} \left[\begin{array}{ccc} 0_{p-m\times r} & 0_{p-m\times n-p-r} & K \end{array}\right]\\ = \left[\begin{array}{c|c} A_{11}^o & \left[\begin{array}{cc} A_{12}^o & A_{121}^m-A_{121}K \end{array}\right]\\\hline 0_{n-m-r\times r} & \left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \end{array}\right] -\left[\begin{array}{c} A_{1221}\\ A_{1222} \end{array}\right] K\left[\begin{array}{cc} 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right] \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-63e4b25f1d738158680736e0e7e80f59_l3.png)
を得るので、![]() の固有値は、
の固有値は、![]() の固有値と
の固有値と
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \end{array}\right]}_{A''} - \underbrace{\left[\begin{array}{c} A_{1221}\\ A_{1222} \end{array}\right]}_{B''} K \underbrace{\left[\begin{array}{cc} 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]}_{C''}\\ (A''\in{\rm\bf R}^{n-m-r\times n-m-r}, B''\in{\rm\bf R}^{n-m-r\times m}, C''\in{\rm\bf R}^{p-m\times n-m-r})\\ =\underbrace{\left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \end{array}\right]}_{A''} - \underbrace{\left[\begin{array}{cc} B''_1 & 0_{n-m-r\times m-m'} \end{array}\right]}_{B''T_m} \underbrace{\left[\begin{array}{cc} K_1\\ K_2 \end{array}\right]}_{T_m^{-1}K} \underbrace{\left[\begin{array}{cc} 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]}_{C''}\\ (T_m\in{\rm\bf R}^{m\times m}, B''_1\in{\rm\bf R}^{n-m-r\times m'}, K_1\in{\rm\bf R}^{m'\times p-m}, K_2\in{\rm\bf R}^{m-m'\times p-m})\\ =A''-B''_1K_1C'' \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f8caf2174f6b6ea2e5a122d260b19c35_l3.png)
の固有値の和となります。ここで、![]() を仮定しています。したがって、まず、
を仮定しています。したがって、まず、![]() の固有値は左半平面にあることが前提となります。
の固有値は左半平面にあることが前提となります。
●そこで、![]() を安定行列とすることができるかを考えます。これは、(低次の)仮想システム
を安定行列とすることができるかを考えます。これは、(低次の)仮想システム
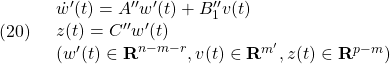
を出力フィードバック
![]()
によって安定化するブレイクダウンした問題となります。そのためにはKimura-Davisonの条件
![]()
が成り立ち、(20)が可制御かつ可観測であることが必要です。後者については、補遺に示すように成り立ちます。ただし、これらは求解条件であって、具体的に![]() を求めるアルゴリズムについては、状態フィードバックのように確立されたものがあるわけではありません。
を求めるアルゴリズムについては、状態フィードバックのように確立されたものがあるわけではありません。
ここまでの手順を、関数ca_form1としてプログラムすることにします。
[4] 以上の準備の下で、![]() の場合のSM制御則をどう決めるかを考えます。(8.3)で定義した、
の場合のSM制御則をどう決めるかを考えます。(8.3)で定義した、
![]()
から次式を得ます。
![]()
ここで、![]() は(12)の
は(12)の![]() が安定行列となるように決めますが、上で調べたように、
が安定行列となるように決めますが、上で調べたように、![]() の固有値は、
の固有値は、![]() の固有値と
の固有値と![]() の固有値の和です。そこで、
の固有値の和です。そこで、![]() は安定行列であることが前提となります。一方
は安定行列であることが前提となります。一方![]() は
は![]() が安定行列となるように決め、
が安定行列となるように決め、
![]()
のように構成します。ここで、![]() は任意でよく、また
は任意でよく、また![]() は(19)で定めた行列です。ちなみに
は(19)で定めた行列です。ちなみに![]() の場合は、
の場合は、![]() は存在せず
は存在せず![]() となり、
となり、![]() の固有値は
の固有値は![]() の固有値だけとなります。
の固有値だけとなります。
●以上では(8.1)に対して、座標変換(10)によって、(11)を得ていました。ここでは、(25)の![]() を用いた次の座標変換を行います(
を用いた次の座標変換を行います(![]() 、
、![]() と置き換え、記法
と置き換え、記法![]() が
が![]() に置き換わっています)。
に置き換わっています)。
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ KC' & I_m \\ \end{array}\right] }_{\bar{T}_s} \underbrace{ \left[\begin{array}{c} {x}''_1(t)\\ {x}''_2(t) \end{array}\right] }_{x''(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} {x}''_1(t)\\ {x}''_2(t) \end{array}\right] }_{x''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -KC' & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ (C'=\left[\begin{array}{cc} 0_{p-m\times n-p} & I_{p-m} \end{array}\right]) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a09e0069834751decee9881760ac9db6_l3.png)
を行うために、まず(26)を(8.1)に代入して
![Rendered by QuickLaTeX.com \displaystyle{(27)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -KC' & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \dot{\bar{x}}''_1(t)\\ \dot{\bar{s}}(t) \end{array}\right] }_{\dot{\bar{x}}''(t)}\\ = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{(T_bT_c)A(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -KC' & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{(T_bT_c)B} u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3b965cc92b91df561d39464b2a06eb0e_l3.png)
左から![]() をかけて
をかけて
![Rendered by QuickLaTeX.com \displaystyle{(28)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\bar{x}}''_1(t)\\ \dot{\bar{s}}(t) \end{array}\right] }_{\dot{\bar{x}}''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ KC' & I_m \end{array}\right] }_{\bar{T}_s} \underbrace{ \left[\begin{array}{cc} A_{11}-A_{12}KC' & A_{12} \\ A_{21}-A_{22}KC' & A_{22} \end{array}\right] }_{(T_bT_c)A(\bar{T}_sT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ + \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ KC' & I_m \end{array}\right] }_{\bar{T}_s} \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3841b7fe89f905ef50150e9e6e841918_l3.png)
すなわち、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(29.1)\quad \underbrace{ \left[\begin{array}{c} \dot{\bar{x}}''_1(t)\\ \dot{\bar{s}}(t) \end{array}\right] }_{\dot{\bar{x}}''(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22} \end{array}\right] }_{\bar{A}=(\bar{T}_sT_bT_c)A(\bar{T}_sT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \bar{B}_2 \end{array}\right] }_{\bar{B}=\bar{T}_sT_bT_cB} u'(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-22de0f3334d3536835a81c4149a15f5a_l3.png)
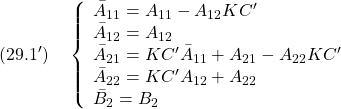
![Rendered by QuickLaTeX.com \displaystyle{(29.2)\quad \begin{array}{l} y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -KC' & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ = \underbrace{ \left[\begin{array}{cc} -TKC' & T \end{array}\right] }_{C(\bar{T}_sT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c45457f5b0c70ff7a60918110f867286_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(29.3)\quad \begin{array}{l} s(t)= \underbrace{ \left[\begin{array}{cc} 0_{m\times n-p} & FT \\ \end{array}\right] }_{FC(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -KC' & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ = \underbrace{ \left[\begin{array}{cc|c} 0_{m\times n-p} & F_1 & F_2 \\ \end{array}\right] }_{FC(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{cc|c} I_{n-p}& 0 & 0\\ 0 & I_{p-m} & 0 \\\hline 0 & -K & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ = \underbrace{ \left[\begin{array}{cc|c} 0_{m\times n-p} & 0_{m\times p-m} & F_2 \\ \end{array}\right] }_{FC(\bar{T}_sT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ (FT=\left[\begin{array}{cc} F_1 & F_2 \end{array}\right], F_1\in{\rm\bf R}^{m\times p-m}, F_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5ebe1bc0632a1704e6bdd06aca89f8c8_l3.png)
●ここからは出力FB型SM制御(p=m)の議論と同様にして、SM制御則として次式を考えます。
![]()
ただし、
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \underbrace{ \left[\begin{array}{cc} 0 & \bar{B}_2^T \end{array}\right] }_{\bar{B}^T} \underbrace{ \left[\begin{array}{cc} P_1 & 0 \\ 0 & P_2 \end{array}\right] }_{P} =F \underbrace{ \left[\begin{array}{cc} -TKC' & T \end{array}\right] }_{\bar{C}}\\ \Rightarrow \bar{B}_2^TP_2=F_2 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-82f76df99883e6d0a1965e87719801b1_l3.png)
![]()
![]()
●以上に基づく設計手順を、数値例で示します。
| MATLAB |
|

図1 出力FB型SM制御のシミュレーション例