| MATLAB |
%of_syn_lmi4.m
%-----
clear all, close all
A=[0 1;-1 -2*0.01]; B=[0;1]; C=[1 0];
%-----
setlmis([]);
R=lmivar(1,[2 1]);
S=lmivar(1,[2 1]);
Ak=lmivar(2,[2 2]);
Bk=lmivar(2,[2 1]);
Ck=lmivar(2,[1 2]);
Dk=lmivar(2,[1 1]);
%-----
alpha=0.1;
lmiPL1=newlmi;
lmiterm([lmiPL1 1 1 R],A,1,'s'); %#2:R*A'+A*R
lmiterm([lmiPL1 1 1 Ck],B,1,'s'); %#2:Ck'*B'+B*Ck
lmiterm([lmiPL1 2 1 Ak],1,1); %#2:Ak
lmiterm([lmiPL1 1 2 0],A); %#2:A
lmiterm([lmiPL1 1 2 Dk],B,C); %#2:B*Dk*C
lmiterm([lmiPL1 2 2 S],1,A,'s'); %#2:A'*S+S*A
lmiterm([lmiPL1 2 2 Bk],1,C,'s'); %#2:C'*Bk'+Bk*C
%
lmiterm([lmiPL1 1 1 R],2*alpha,1); %#2:2*alpha*R
lmiterm([lmiPL1 2 1 0],2*alpha); %#2:2*alpha*I
lmiterm([lmiPL1 2 2 S],2*alpha,1); %#2:2*alpha*S
%-----
r=5;
lmiPL2=newlmi;
lmiterm([lmiPL2 1 1 R],-r,1); %#3:-r*R
lmiterm([lmiPL2 2 1 0],-r); %#3:-r*I
lmiterm([lmiPL2 2 2 S],-r,1); %#3:-r*S
%
lmiterm([lmiPL2 1 3 R],A,1); %#3:A*R
lmiterm([lmiPL2 1 3 Ck],B,1); %#3:B*Ck
lmiterm([lmiPL2 2 3 Ak],1,1); %#3:Ak
lmiterm([lmiPL2 1 4 0],A); %#3:A
lmiterm([lmiPL2 1 4 Dk],B,C); %#3:B*Dk*C
lmiterm([lmiPL2 2 4 S],1,A); %#3:S*A
lmiterm([lmiPL2 2 4 Bk],1,C); %#3:Bk*C
%
lmiterm([lmiPL2 3 3 R],-r,1); %#3:-r*R
lmiterm([lmiPL2 4 3 0],-r); %#3:-r*I
lmiterm([lmiPL2 4 4 S],-r,1); %#3:-r*S
%-----
th=pi/2; sth=sin(th); cth=cos(th);
lmiPL3=newlmi;
lmiterm([lmiPL3 1 1 R],sth*A,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL3 1 1 Ck],sth*B,1,'s'); %#4:sth*(Ck'*B'+B*Ck)
lmiterm([lmiPL3 2 1 Ak],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL3 1 2 0],sth*A); %#4:sth*(A)
lmiterm([lmiPL3 1 2 Dk],sth*B,C); %#4:sth*(B*Dk*C)
lmiterm([lmiPL3 2 2 S],1,sth*A,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL3 2 2 Bk],1,sth*C,'s'); %#4:sth*(C'*Bk'+Bk*C)
%
%lmiterm([lmiPL3 1 3 R],1,cth*A'); %#1:cth*(R*A')
%lmiterm([lmiPL3 1 3 R],-cth*A,1); %#1:cth*(-A*R)
%lmiterm([lmiPL3 1 3 -Ck],cth*B',1); %#1:cth*(Ck'*B')
%lmiterm([lmiPL3 1 3 Ck],-cth*B,1); %#1:cth*(-B*Ck)
lmiterm([lmiPL3 1 3 R],cth*A,1); %#1:cth*(A*R)
lmiterm([lmiPL3 1 3 R],1,-cth*A'); %#1:cth*(-R*A')
lmiterm([lmiPL3 1 3 Ck],cth*B,1); %#1:cth*(B*Ck)
lmiterm([lmiPL3 1 3 -Ck],-cth*B',1); %#1:cth*(-Ck'*B')
lmiterm([lmiPL3 2 3 Ak],cth,1); %#4:cth*(Ak)
lmiterm([lmiPL3 1 4 -Ak],-cth,1); %#4:cth*(-Ak')
lmiterm([lmiPL3 1 4 0],A); %#4:cth*(A)
lmiterm([lmiPL3 2 3 0],-A'); %#4:cth*(-A')
lmiterm([lmiPL3 1 4 Dk],cth*B,C); %#4:cth*(B*Dk*C)
lmiterm([lmiPL3 2 3 -Dk],-cth*C',B'); %#4:cth*(-C'*Dk'*B')
lmiterm([lmiPL3 2 4 S],1,cth*A); %#4:cth*(S*A)
lmiterm([lmiPL3 2 4 S],-cth*A',1); %#4:cth*(-A'*S)
lmiterm([lmiPL3 2 4 Bk],1,cth*C); %#4:cth*(Bk*C)
lmiterm([lmiPL3 2 4 -Bk],-cth*C',1); %#4:cth*(-C'*Bk')
%
lmiterm([lmiPL3 3 3 R],sth*A,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL3 3 3 Ck],sth*B,1,'s'); %#4:sth*(Ck'*B'+B*Ck)
lmiterm([lmiPL3 4 3 Ak],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL3 3 4 0],sth*A); %#4:sth*(A)
lmiterm([lmiPL3 3 4 Dk],sth*B,C); %#4:sth*(B*Dk*C)
lmiterm([lmiPL3 4 4 S],1,sth*A,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL3 4 4 Bk],1,sth*C,'s'); %#4:sth*(C'*Bk'+Bk*C)
%-----
posX=-newlmi;
lmiterm([posX 1 1 R],1,1); %#5:R
lmiterm([posX 2 1 0],1); %#5:I
lmiterm([posX 2 2 S],1,1); %#5:S
%-----
LMIs=getlmis;
[tmin,xfeas]=feasp(LMIs);
R=dec2mat(LMIs,xfeas,R);
S=dec2mat(LMIs,xfeas,S);
ak=dec2mat(LMIs,xfeas,Ak);
bk=dec2mat(LMIs,xfeas,Bk);
ck=dec2mat(LMIs,xfeas,Ck);
dk=dec2mat(LMIs,xfeas,Dk);
[u,sd,v]=svd(eye(size(A,1)-S*R);
sd=diag(sqrt(1./diag(sd)));
Ni=sd*u'; Mti=v*sd;
AK=Ni*(ak-S*(A-B*dk*C)*R-bk*C*R-S*B*ck)*Mti;
BK=Ni*(bk-S*B*dk);
CK=(ck-dk*C*R)*Mti;
DK=dk;
%-----
pl=eig(A)
ACL=[A+B*DK*C B*CK;
BK*C AK];
plCL=eig(ACL)
figure(1)
dregion(0,0,5,0.4*pi,5*[-1,1,-1,1])
plot(real(pl),imag(pl),'x',real(plCL),imag(plCL),'*')
%-----
%eof
|
![]() 次系
次系![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \left[\begin{array}{c} \dot{x} \\ \dot{x}_K \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} A+BD_KC & BC_K \\ B_KC & A_K \end{array}\right] }_{A_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b4fa3fc3acef0120663cbc7929c84396_l3.png)
![]()
![]() を求める問題を考えます。
を求める問題を考えます。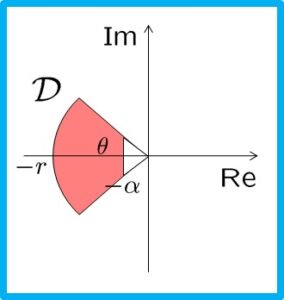
![]()
![]() となるLMI条件は、次の通りでした。
となるLMI条件は、次の通りでした。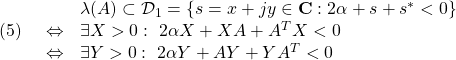
![]() となるLMI条件は、次のようになります。
となるLMI条件は、次のようになります。![]()
![]() を代入して
を代入して![]()
![]() 、右から
、右から![]() をかけると、次のようなLMIとなります。
をかけると、次のようなLMIとなります。![]()
![]() を求め、次式によって出力フィードバックのゲインを決定します。
を求め、次式によって出力フィードバックのゲインを決定します。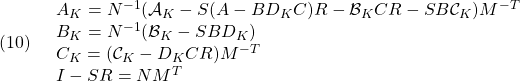
![]() となるLMI条件は、次の通りでした。
となるLMI条件は、次の通りでした。![Rendered by QuickLaTeX.com \displaystyle{(11) \begin{array}{lll} &&\lambda(A)\subset {\cal D}_2=\{s=x+jy\in{\rm\bf C}: \left[\begin{array}{cc} -r & s \\ s^* & -r \end{array}\right] <0 \}\nonumber\\ &\Leftrightarrow& \exists X>0:\ \left[\begin{array}{cc} -rX & XA \\ A^TX & -rX \end{array}\right]<0 \nonumber\\ &\Leftrightarrow& \exists Y>0:\ \left[\begin{array}{cc} -rY & AY \\ YA^T & -rY \end{array}\right]<0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cef2a962a3396f8afb1b770218baf02b_l3.png)
![]() となるLMI条件は、次のようになります。
となるLMI条件は、次のようになります。![]()
![]() を代入して
を代入して![]()
![]() 、右から
、右から![]() をかけると、次のようなLMIとなります。
をかけると、次のようなLMIとなります。![]()
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{cc} -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] & \left[\begin{array}{cc} AR+B{\cal C}_K & A+BD_KC \\ {\cal A}_K & SA+{\cal B}_KC \end{array}\right] \\ \left[\begin{array}{cc} AR+B{\cal C}_K & A+BD_KC \\ {\cal A}_K & SA+{\cal B}_KC \end{array}\right]^T & -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] \end{array}\right] <0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8ee8a916fb01e341b6b05b9dec8adee2_l3.png)
![]() を求め、次式によって出力フィードバックのゲインを決定します。
を求め、次式によって出力フィードバックのゲインを決定します。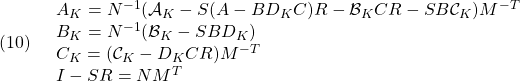
![]() となるLMI条件は、次の通りでした。
となるLMI条件は、次の通りでした。![Rendered by QuickLaTeX.com \displaystyle{(16) \begin{array}{lll} &&\lambda(A)\subset {\cal D}_3=\{s=x+jy\in{\rm\bf C}:\\ && \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]s + \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]^Ts^* <0 \}\nonumber\\ &&\Leftrightarrow \exists X>0:\ \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] <0 \nonumber\\ &&\Leftrightarrow \exists Y>0:\ \left[\begin{array}{cc} \sin\theta(AY+YA^T) & \cos\theta(AY-YA^T) \\ -\cos\theta(AY-YA^T) & \sin\theta(AY+YA^T) \end{array}\right] <0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bfd97f662a8d6ff7c86a2dec2b62b921_l3.png)
![]() となるLMI条件は、次のようになります。
となるLMI条件は、次のようになります。![]()
![]()
![]() を代入して
を代入して![]()
![]()
![]() 、右から
、右から![]() をかけると、次のようなLMIとなります。
をかけると、次のようなLMIとなります。![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad \begin{array}{l} \exists \left[\begin{array}{cc} R & I \\ I & S \end{array}\right]>0:\ \\ \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right] \otimes \left[\begin{array}{cc} AR+B{\cal C}_K & A+BD_KC \\ {\cal A}_K & SA+{\cal B}_KC \end{array}\right]+ \\ (\left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right] \otimes \left[\begin{array}{cc} AR+B{\cal C}_K & A+BD_KC \\ {\cal A}_K & SA+{\cal B}_KC \end{array}\right])^T <0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-405aa571dd83441fa45f2e21e96b3c03_l3.png)
![]() を求め、次式によって出力フィードバックのゲインを決定します。
を求め、次式によって出力フィードバックのゲインを決定します。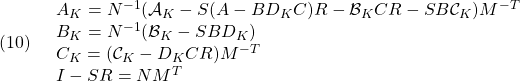
![]() 次のコードを参考にして、
次のコードを参考にして、![]() を達成する出力FBを求める関数を作成せよ。
を達成する出力FBを求める関数を作成せよ。