出力FB用変数変換…Homework
[1] ![]() 次系
次系
![]()
に対する出力フィードバック
![]()
による閉ループ系
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \left[\begin{array}{c} \dot{x} \\ \dot{x}_K \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} A+BD_KC & BC_K \\ B_KC & A_K \end{array}\right] }_{A_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b4fa3fc3acef0120663cbc7929c84396_l3.png)
を考えます。
出力フィードバックに関する変数変換として、以下の議論が知られています。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} S & N \\ N^T & S' \end{array}\right] }_{X_{CL}} \underbrace{ \left[\begin{array}{cc} R & M \\ M^T & R' \end{array}\right] }_{Y_{CL}=X^{-1}_{CL}} = \left[\begin{array}{cc} I & 0 \\ 0 & I \end{array}\right] \quad(SR+NM^T=I)\\ \underbrace{ \left[\begin{array}{cc} R & M \\ M^T & R' \end{array}\right] }_{Y_{CL}} \underbrace{ \left[\begin{array}{cc} S & N \\ N^T & S' \end{array}\right] }_{X_{CL}=Y^{-1}_{CL}} = \left[\begin{array}{cc} I & 0 \\ 0 & I \end{array}\right] \quad(RS+MN^T=I) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fd01714fd5e49b60bc3e606ac49694bb_l3.png)
が与えられるとき、次の命題が成立します(Note B41参照)。
![]()
このとき、次が成り立ちます。
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad X_{CL}= \underbrace{ \left[\begin{array}{cc} I & S \\ 0 & N^T \end{array}\right] }_{\Pi_2} \underbrace{ \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right]^{-1} }_{\Pi_1^{-1}} = \underbrace{ \left[\begin{array}{cc} R & M \\ I & 0 \end{array}\right]^{-1} }_{\Pi_1^{-T}} \underbrace{ \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] }_{\Pi_2^T} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c03ff30c1097edc6cffd80c6cbec396d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad Y_{CL}= \underbrace{ \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right] }_{\Pi_1} \underbrace{ \left[\begin{array}{cc} I & S \\ 0 & N^T \end{array}\right]^{-1} }_{\Pi_2^{-1}} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right]^{-1} }_{\Pi_2^{-T}} \underbrace{ \left[\begin{array}{cc} R & M \\ I & 0 \end{array}\right] }_{\Pi_1^T} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6f5ea3d73a1aa4cea557b17a0bec6ba5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] = \underbrace{ \left[\begin{array}{cc} R & M \\ I & 0 \end{array}\right] }_{\Pi_1^T} \underbrace{ \left[\begin{array}{cc} I & S \\ 0 & N^T \end{array}\right] }_{\Pi_2} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] }_{\Pi_2^T} \underbrace{ \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right] }_{\Pi_1} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-01f14a656f5f1a28a0df2c534bc39542_l3.png)
以下では、次の変換を用います。
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{l} \Pi_2^TA_{CL}\Pi_1= \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} A+BD_KC & BC_K \\ B_KC & A_K \end{array}\right] \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right] \\ =\left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} (A+BD_KC)R+BC_KM^T & A+BD_KC \\ B_KCR+A_KM^T & B_KC \end{array}\right] \\ =\left[\begin{array}{ccc} (A+BD_KC)R+BC_KM^T & \\ S(A+BD_KC)R+SBC_KM^T+NB_KCR+NA_KM^T & \end{array}\right. \\ \left.\begin{array}{ccc} & A+BD_KC \\ & S(A+BD_KC)+NB_KC \end{array}\right] \\ =\left[\begin{array}{cc} AR+B{\cal C}_K & A+BD_KC \\ {\cal A}_K & SA+{\cal B}_KC \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7768573f62703ece20c21171c0e69882_l3.png)
ただし
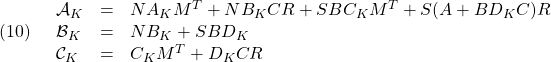
[2] ![]() となるLMI条件は、次の通りでした。
となるLMI条件は、次の通りでした。
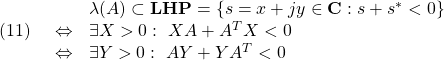
したがって、![]() となるLMI条件は、次のようになります。
となるLMI条件は、次のようになります。
![]()
![]() を代入して
を代入して
![]()
左から![]() 、右から
、右から![]() をかけると、次のようなLMIとなります。
をかけると、次のようなLMIとなります。
![]()
すなわち
|
|
これを解いて ![]() を求め、次式によって出力フィードバックのゲインを決定します。
を求め、次式によって出力フィードバックのゲインを決定します。
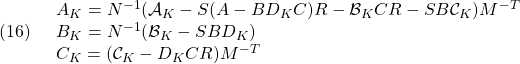
|
ただし、![]() と
と![]() は次の分解を行って求めます。
は次の分解を行って求めます。
![]()
または、![]() に注意して
に注意して
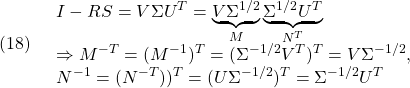
演習B41…Flipped Classroom
![]() 次のコードを参考にして、安定化出力FBを求める関数を作成せよ。
次のコードを参考にして、安定化出力FBを求める関数を作成せよ。
| MATLAB |
|
Note B41 補題
● ![]()
|
|
実際
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \exists U_{PQ}:\ \left[\begin{array}{c} P \\ Q \end{array}\right]U_{PQ}=0 \quad\Rightarrow\quad \left\{\begin{array}{l} \exists U_{P}:\ P\underbrace{ \left[\begin{array}{cc} U_{PQ} & U_P \end{array}\right] }_{W_P}=0\\ \exists U_{Q}:\ Q\underbrace{ \left[\begin{array}{cc} U_{PQ} & U_Q \end{array}\right] }_{W_Q}=0\\ \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-732e424cb0a0b6856203c2887f795534_l3.png)
を満足する![]() を定めますと、次が成り立ちます。
を定めますと、次が成り立ちます。
![]()
この![]() を用いて次が成り立ちます。
を用いて次が成り立ちます。
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \Leftrightarrow \left[\begin{array}{cccc} \Psi_{11} & \Psi_{12} & \Psi_{13} & \Psi_{14} \\ \Psi_{12}^T & \Psi_{22} & \Psi_{23}& \Psi_{24}\\ \Psi_{13}^T & \Psi_{23}^T & \Psi_{33} & \Psi_{34}\\ \Psi_{14}^T & \Psi_{24}^T & \Psi_{34}^T & \Psi_{44} \end{array}\right] +\left[\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & \Theta_{11}^T & 0 & \Theta_{12}^T \\ 0 & \Theta_{21}^T & 0 & \Theta_{22}^T \end{array}\right] +\left[\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & \Theta_{11} & \Theta_{21} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & \Theta_{12} & \Theta_{22} \end{array}\right] < 0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8df35b0d0eded8e0048a0d63693847dc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \Leftrightarrow \left[\begin{array}{ccc|c} \Psi_{11} & \Psi_{12} & \Psi_{13} & \Psi_{14} \\ \Psi_{12}^T & \Psi_{22} & \Psi_{23}+\Theta_{11} & \Psi_{24}+\Theta_{21} \\ \Psi_{13}^T & \Psi_{23}^T+\Theta_{11}^T & \Psi_{33} & \Psi_{34}+\Theta_{12} \\ \hline \Psi_{14}^T & \Psi_{24}^T+\Theta_{21}^T & \Psi_{34}^T+\Theta_{12}^T & \Psi_{44}+\Theta_{22}+\Theta_{22}^T \end{array}\right]<0}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c38812ba3c2440e987782ee4c75177a3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{\Leftrightarrow \left\{\begin{array}{l} \left[\begin{array}{cccc} \Psi_{11} & \Psi_{12} & \Psi_{13} \\ \Psi_{12}^T & \Psi_{22} & \Psi_{23}+\Theta_{11} \\ \Psi_{13}^T & \Psi_{23}^T+\Theta_{11}^T & \Psi_{33} \end{array}\right] < 0 \\ \quad\\ \Psi_{44}+\Theta_{22}+\Theta_{22}^T-\\ \left[\begin{array}{c} \Psi_{14} \\ \Psi_{24}+\Theta_{21} \\ \Psi_{34}+\Theta_{12} \end{array}\right]^T \left[\begin{array}{cccc} \Psi_{11} & \Psi_{12} & \Psi_{13} \\ \Psi_{12}^T & \Psi_{22} & \Psi_{23}+\Theta_{11} \\ \Psi_{13}^T & \Psi_{23}^T+\Theta_{11}^T & \Psi_{33} \end{array}\right]^{-1} \left[\begin{array}{c} \Psi_{14} \\ \Psi_{24}+\Theta_{21}^T \\ \Psi_{34}+\Theta_{12}^T \end{array}\right] < 0 \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0b09c3219c54b4e57f477f9e1f9a5cfa_l3.png)
この第2式は、与えられた![]() に対して、
に対して、![]() を適当に選んで、常に満足させることができます。一方、第1式は
を適当に選んで、常に満足させることができます。一方、第1式は
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \left[\begin{array}{ccc} I & 0 & 0 \\ -\Psi_{12}^T\Psi_{11}^{-1} & I & 0 \\ -\Psi_{13}^T\Psi_{11}^{-1} & 0 & I \end{array}\right] \left[\begin{array}{cccc} \Psi_{11} & \Psi_{12} & \Psi_{13} \\ \Psi_{12}^T & \Psi_{22} & \Psi_{23}+\Theta_{11} \\ \Psi_{13}^T & \Psi_{23}^T+\Theta_{11}^T & \Psi_{33} \end{array}\right]\\ \times \left[\begin{array}{ccc} I & -\Psi_{11}^{-1}\Psi_{12} & -\Psi_{11}^{-1}\Psi_{13} \\ 0 & I & 0 \\ 0 & 0 & I \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1e76c8b05c4fec546ea5dcaeb7bc0880_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \Leftrightarrow \left[\begin{array}{ccc} \Psi_{11} & 0 & 0 \\ 0 & \Psi_{22}-\Psi_{12}^T\Psi_{11}^{-1}\Psi_{12} & \Theta_{11}+\Psi_{23}-\Psi_{12}^T\Psi_{11}^{-1}\Psi_{13} \\ 0 & \Theta_{11}^T+\Psi_{23}^T-\Psi_{13}^T\Psi_{11}^{-1}\Psi_{12} & \Psi_{33}-\Psi_{13}^T\Psi_{11}^{-1}\Psi_{13} \end{array}\right] < 0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ae8fb6d275c9abbf9f70e0b28fd49f9d_l3.png)
ここで、![]() を
を
![]()
を満足するように選ぶと、次の条件を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{ \left[\begin{array}{cc} \Psi_{11} & \Psi_{12} \\ \Psi_{12}^T & \Psi_{22} \end{array}\right] }_{W_P^T\Psi W_P} < 0,\ \underbrace{ \left[\begin{array}{cc} \Psi_{11} & \Psi_{13} \\ \Psi_{13}^T & \Psi_{33} \end{array}\right] }_{W_Q^T\Psi W_Q}< 0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-19e320b41b055e34b3fc56bc65f0f8a1_l3.png)
● ![]()
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} S & N \\ X & S' \end{array}\right] }_{W} \underbrace{ \left[\begin{array}{cc} R & M \\ Y & R' \end{array}\right] }_{V=W^{-1}} = \left[\begin{array}{cc} I & 0 \\ 0 & I \end{array}\right] \quad(I=SR+NY=SR-NS'^{-1}XR)\\ \underbrace{ \left[\begin{array}{cc} R & M \\ Y & R' \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} S & N \\ X & S' \end{array}\right] }_{W=V^{-1}} = \left[\begin{array}{cc} I & 0 \\ 0 & I \end{array}\right] \quad(I=RS+MX=RS-MR'^{-1}YS) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3448bb3b806d0ccacda7242882b9895e_l3.png)
が与えられるとき、次が成り立ちます。
|
|
実際
![]()
に注意して
![]()
のように分解し、![]() と選ぶと
と選ぶと
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad 0< \underbrace{ \left[\begin{array}{cc} S & L_{\ell}S' \\ L_r & S' \end{array}\right] }_W + \underbrace{ \left[\begin{array}{cc} S^T & L_r^T \\ S'\,^TL_{\ell}^T & S'\,^T \end{array}\right] }_{W^T} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-de6dadd7dd24bb41f9f007525cb9b86a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \underbrace{ \left[\begin{array}{cc} S+S^T & L_r^T \\ L_r & 0 \end{array}\right] }_{\Psi} + \underbrace{ \left[\begin{array}{c} 0 \\ I \end{array}\right] }_{P^T} \underbrace{ S'\,^T }_{\Theta^T} \underbrace{ \left[\begin{array}{cc} L_\ell^T & I \end{array}\right] }_{Q} + \underbrace{ \left[\begin{array}{c} L_{\ell} \\ I \end{array}\right] }_{Q^T} \underbrace{ S' }_{\Theta} \underbrace{ \left[\begin{array}{cc} 0 & I \end{array}\right] }_{P}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e1f30f8f2b570b7c38a37a83dd1e92fa_l3.png)
![Rendered by QuickLaTeX.com \Leftrightarrow \left\{\begin{array}{l} \underbrace{ \left[\begin{array}{cc} I & 0 \end{array}\right] }_{W_P^T} \underbrace{ \left[\begin{array}{cc} S+S^T & L_r^T \\ L_r & 0 \end{array}\right] }_{\Psi} \underbrace{ \left[\begin{array}{c} I \\ 0 \end{array}\right] }_{W_P}<0 \quad (\underbrace{ \left[\begin{array}{cc} 0 & I \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} I \\ 0 \end{array}\right] }_{W_P}=0)\\ \underbrace{ \left[\begin{array}{cc} I & -L_\ell \end{array}\right] }_{W_Q^T} \underbrace{ \left[\begin{array}{cc} S+S^T & L_r^T \\ L_r & 0 \end{array}\right] }_{\Psi} \underbrace{ \left[\begin{array}{c} I \\ -L_\ell^T \end{array}\right] }_{W_Q}<0 \quad (\underbrace{ \left[\begin{array}{cc} L_\ell^T & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} I \\ -L_\ell^T \end{array}\right] }_{W_Q}=0)\\ \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f2b8bbeeeaa60f811e8eae65ea966250_l3.png)
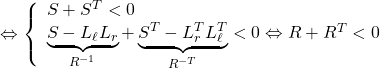
一方、
![]()
のように分解し、![]() と選ぶと
と選ぶと
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad 0< \underbrace{ \left[\begin{array}{cc} R & L_{\ell}R' \\ L_r & R' \end{array}\right] }_V + \underbrace{ \left[\begin{array}{cc} R^T & L_r^T \\ R'\,^TL_{\ell}^T & R'\,^T \end{array}\right] }_{V^T} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f99b468e094a204216d80c309b78f582_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \underbrace{ \left[\begin{array}{cc} R+R^T & L_r^T \\ L_r & 0 \end{array}\right] }_{\Psi} + \underbrace{ \left[\begin{array}{c} 0 \\ I \end{array}\right] }_{P^T} \underbrace{ R'\,^T }_{\Theta^T} \underbrace{ \left[\begin{array}{cc} L_\ell^T & I \end{array}\right] }_{Q} + \underbrace{ \left[\begin{array}{c} L_{\ell} \\ I \end{array}\right] }_{Q^T} \underbrace{ R' }_{\Theta} \underbrace{ \left[\begin{array}{cc} 0 & I \end{array}\right] }_{P}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-77ba77917ab5a14d39db909ea189fa99_l3.png)
![Rendered by QuickLaTeX.com \Leftrightarrow \left\{\begin{array}{l} \underbrace{ \left[\begin{array}{cc} I & 0 \end{array}\right] }_{W_P^T} \underbrace{ \left[\begin{array}{cc} R+R^T & L_r^T \\ L_r & 0 \end{array}\right] }_{\Psi} \underbrace{ \left[\begin{array}{c} I \\ 0 \end{array}\right] }_{W_P}<0 \quad (\underbrace{ \left[\begin{array}{cc} 0 & I \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} I \\ 0 \end{array}\right] }_{W_P}=0)\\ \underbrace{ \left[\begin{array}{cc} I & -L_\ell \end{array}\right] }_{W_Q^T} \underbrace{ \left[\begin{array}{cc} R+R^T & L_r^T \\ L_r & 0 \end{array}\right] }_{\Psi} \underbrace{ \left[\begin{array}{c} I \\ -L_\ell^T \end{array}\right] }_{W_Q}<0 \quad (\underbrace{ \left[\begin{array}{cc} L_\ell^T & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} I \\ -L_\ell^T \end{array}\right] }_{W_Q}=0)\\ \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9c87357de622e87966262b65b5d6b291_l3.png)
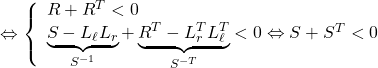
●特に、![]() かつ
かつ
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} S & N \\ N^T & S' \end{array}\right] }_W \underbrace{ \left[\begin{array}{cc} R & M \\ M^T & R' \end{array}\right] }_{V=W^{-1}} = \left[\begin{array}{cc} I & 0 \\ 0 & I \end{array}\right] \quad(SR+NM^T=I) \\ \underbrace{ \left[\begin{array}{cc} R & M \\ M^T & R' \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} S & N \\ N^T & S' \end{array}\right] }_{W=V^{-1}} = \left[\begin{array}{cc} I & 0 \\ 0 & I \end{array}\right] \quad(RS+MN^T=I) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b5af46c0250be9099f8d39a21a2c9d18_l3.png)
のときは
![]()
となりますが、![]() と
と![]() は
は
![]()
を考慮して、次の命題を得ます。
|
|
●以上では、次のシュール補元に関する公式を多用しました。
![Rendered by QuickLaTeX.com \displaystyle{\boxed{ \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]<0\\ &\Leftrightarrow& P-MQ^{-1}M^T<0,\ Q<0\\ &\Leftrightarrow& P<0,\ Q-M^TP^{-1}M<0 \end{array} }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4efd2df144b4ea2e4b5c0dd6970ed0ac_l3.png) |
![Rendered by QuickLaTeX.com \displaystyle{\boxed{ \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]>0\\ &\Leftrightarrow& MQ^{-1}M^T-P>0,\ Q>0\\ &\Leftrightarrow& P>0,\ M^TP^{-1}M-Q>0 \end{array} }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ff8466bc18b10c46d2a1973fde841fb2_l3.png) |