●原、千田、佐伯、野波:ロバスト制御のためのベンチマーク問題(I)
-3慣性系に対する位置制御・速度制御
●佐伯、千田、野波、原:ロバスト制御のためのベンチマーク問題(II)
-位置制御系の設計例
[1] 次図のような3慣性系を考えます。
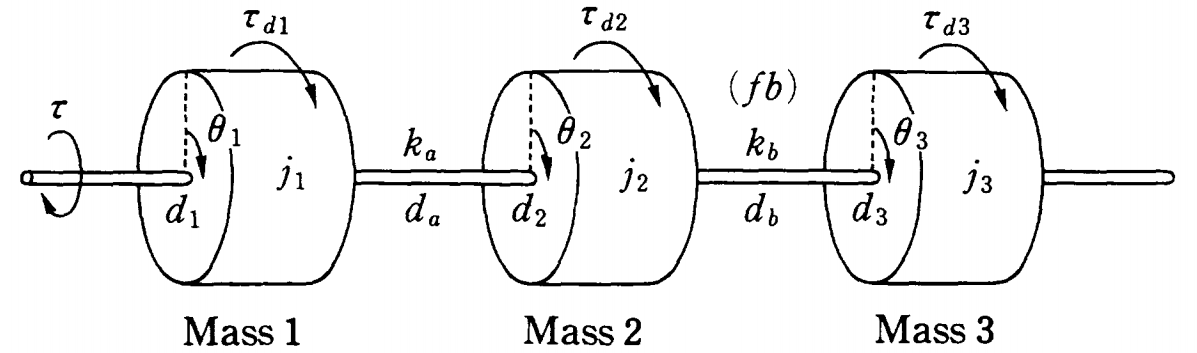
これは次の運動方程式で表されます。
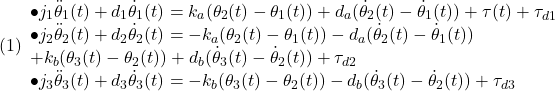
ここで、物理定数は次の値が想定されています。
| 物理定数 | 最小値 | 公称値 | 最大値 |
| 0.0009 | 0.001 | 0.0011 | |
| 0.0009 | 0.001 | 0.0011 | |
| 0.001 | 0.002 | 0.003 | |
| 0.045 | 0.05 | 0.055 | |
| 0.0009 | 0.001 | 0.0011 | |
| 0.0014 | 0.007 | 0.035 | |
| 0.0002 | 0.001 | 0.01 | |
| 0.0009 | 0.001 | 0.0011 | |
| 828 | 920 | 1012 | |
| 72 | 80 | 88 |
●以下では、![]() の3つのパラメータ誤差を考慮して、回転体3に対してインパルス外乱が加わるときのシミュレーションを行ってみます。
の3つのパラメータ誤差を考慮して、回転体3に対してインパルス外乱が加わるときのシミュレーションを行ってみます。
図1
原論文にはさまざまな問題設定がなされていますが、ここでは、回転体3に対するインパルス外乱の下で、回転体3を速やかに整定させる制御系設計を検討します。ただし、操作入力には次の振幅制限
![]()
が課され、観測出力は回転体1の変位![]() とします。
とします。
[2] 制御対象のLPVモデルを導出します。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{ccc} j_1 & 0 & 0\\ 0 & j_2 & 0\\ 0 & 0 & j_3 \end{array}\right] }_{J} \underbrace{ \left[\begin{array}{ccc} \ddot{\theta}_1(t)\\ \ddot{\theta}_2(t)\\ \ddot{\theta}_3(t) \end{array}\right] }_{\ddot{\xi}(t)} +\underbrace{ \left[\begin{array}{ccc} d_1+d_a & -d_a & 0\\ -d_a & d_2+d_a+d_b & -d_b\\ 0 & -d_b & d_3+d_b \end{array}\right] }_{D} \underbrace{ \left[\begin{array}{ccc} \dot{\theta}_1(t)\\ \dot{\theta}_2(t)\\ \dot{\theta}_3(t) \end{array}\right] }_{\dot{\xi}(t)}\\ +\underbrace{ \left[\begin{array}{ccc} k_a & -k_a & 0\\ -k_a & k_a+k_b & -k_b\\ 0 & -k_b & k_b \end{array}\right] }_{K} \underbrace{ \left[\begin{array}{ccc} {\theta}_1(t)\\ {\theta}_2(t)\\ {\theta}_3(t) \end{array}\right] }_{{\xi}(t)} = \underbrace{ \left[\begin{array}{ccc} 1\\ 0\\ 0 \end{array}\right] }_{E_{3\times1}}\tau(t) +\underbrace{ \left[\begin{array}{ccc} \tau_{d1}\\ \tau_{d2}\\ \tau_{d3} \end{array}\right] }_{\tau_{d}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f503c942853f86278fa2c1b5860489f2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \left[\begin{array}{c} \dot{\xi}(t)\\ \ddot{\xi}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0_{3\times3} & I_3\\ -J^{-1}K & -J^{-1}D \end{array}\right] }_{A(d_3/j_3,k_b/j_3)} \left[\begin{array}{c} {\xi}(t)\\ \dot{\xi}(t) \end{array}\right] + \left[\begin{array}{c} 0\\ J^{-1}E_{3\times1} \end{array}\right]\tau(t) + \left[\begin{array}{c} 0\\ J^{-1} \end{array}\right]\tau_d \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b27ed5b2207cc572494ae4bfcb986605_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} J^{-1}D={ \left[\begin{array}{ccc} d_1/j_1+d_a/j_1 & -d_a/j_1 & 0\\ -d_a/j_2 & d_2/j_2+d_a/j_2+d_b/j_2 & -d_b/j_2\\ 0 & -d_b/j_3 & d_3/j_3+d_b/j_3 \end{array}\right]\\ =(d_1/j_1)D_1+(d_2/j_2)D_2+(d_3/j_3)D_3\\ +(d_a/j_1)D_4+(d_a/j_2)D_5+(d_b/j_2)D_6+(d_b/j_3)D_7\\ J^{-1}K= \left[\begin{array}{ccc} k_a/j_1 & -k_a/j_1 & 0\\ -k_a/j_2 & k_a/j_2+k_b/j_2 & -k_b/j_2\\ 0 & -k_b/j_3 & k_b/j_3 \end{array}\right]\\ =(k_a/j_1)K_1+(k_a/j_2)K_2+(k_b/j_2)K_3+(k_b/j_3)K_4\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e79c3e7ebe83b4bd6c5f805aa18b7707_l3.png)
![]()
ここで、![]() 、
、![]() に対する次の内分式に注目します。
に対する次の内分式に注目します。
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \left[\begin{array}{c} \alpha\\ \beta \end{array}\right]= \underbrace{\frac{\alpha_2-\alpha}{\alpha_2-\alpha_1}\frac{\beta_2-\beta}{\beta_2-\beta_1}}_{p_{11}(\alpha,\beta)}\left[\begin{array}{c} \alpha_1\\ \beta_1 \end{array}\right]+ \underbrace{\frac{\alpha_2-\alpha}{\alpha_2-\alpha_1}\frac{\beta-\beta_1}{\beta_2-\beta_1}}_{p_{12}(\alpha,\beta)}\left[\begin{array}{c} \alpha_1\\ \beta_2 \end{array}\right]\\+ \underbrace{\frac{\alpha-\alpha_1}{\alpha_2-\alpha_1}\frac{\beta_2-\beta}{\beta_2-\beta_1}}_{p_{21}(\alpha,\beta)}\left[\begin{array}{c} \alpha_2\\ \beta_1 \end{array}\right]+ \underbrace{\frac{\alpha-\alpha_1}{\alpha_2-\alpha_1}\frac{\beta-\beta_1}{\beta_2-\beta_1}}_{p_{22}(\alpha,\beta)}\left[\begin{array}{c} \alpha_2\\ \beta_2 \end{array}\right] \\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-484fd6de8261d6cb87bf54fb54115386_l3.png)
![]()
![]() のとき上の状態方程式は、端点モデル
のとき上の状態方程式は、端点モデル
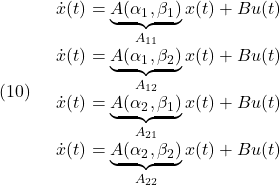
を、![]() によって重み付けして、LPVモデル
によって重み付けして、LPVモデル
![]()
として表されます。
[3] 状態FB
図2
[3] 出力FB
図3
演習13.3…Flipped Classroom
![]() 図1
図1
| MATLAB | |
| SCILAB |
![]() 図2
図2
| MATLAB | |
| SCILAB |
![]() 図3
図3
| MATLAB | |
| SCILAB |