倒立振子

投稿日時: 投稿者:

倒立振子…Homework

倒立振子は制御なしには平衡状態を保てないので、制御技術の有効性を示すのに、よく研究されています。次図は様々な倒立振子を示しています。

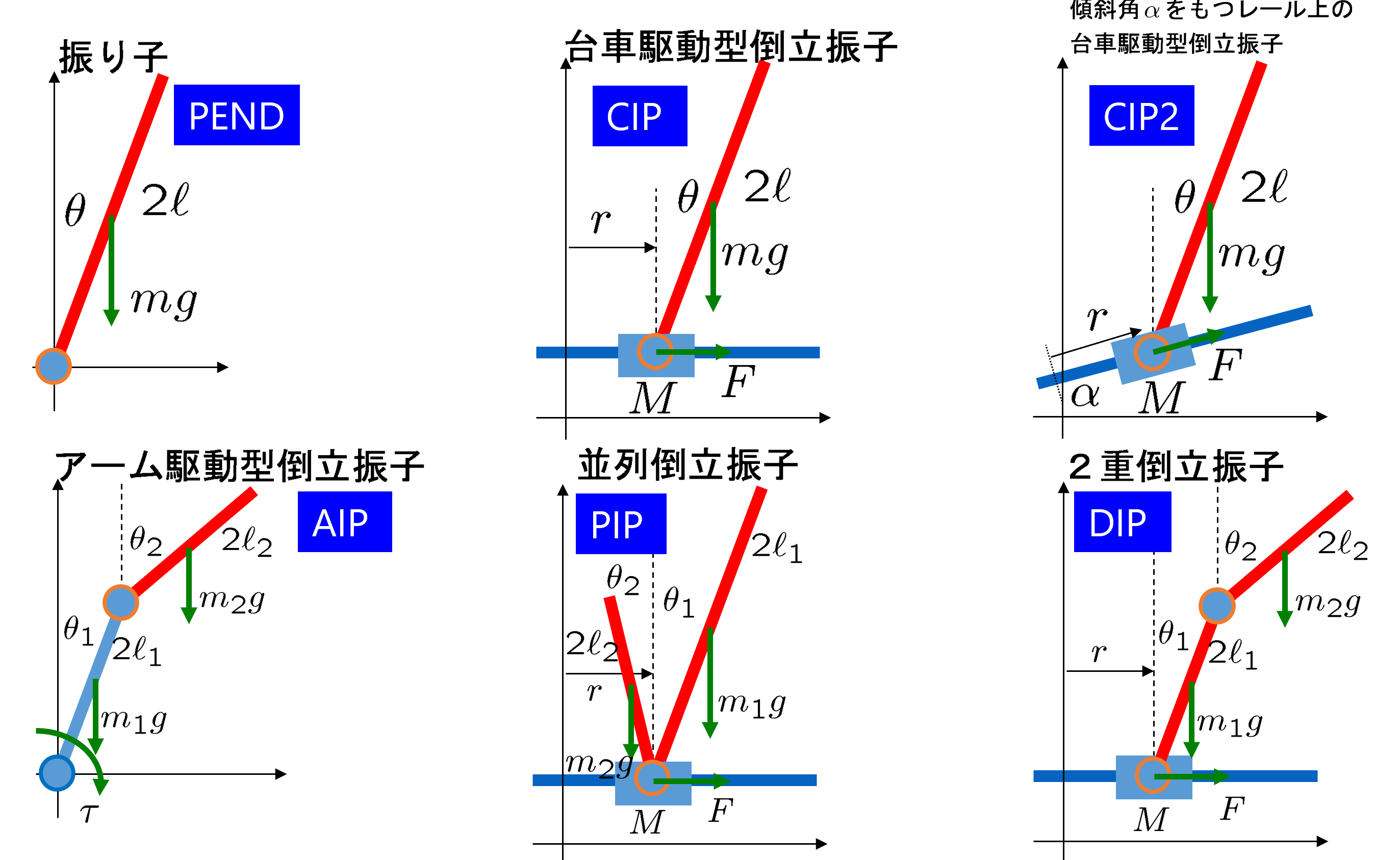図1 様々な倒立振子

これらの倒立振子について、まずは非線形シミュレータを開発する必要があります。以下に、要点だけを示しておきます。いずれも振子の角度は上向きの鉛直線から時計回りを正としています。

[1] PEND
1^\circ 運動方程式の導出（数式処理の利用）
\displaystyle{(1.1)\quad \ddot{\theta}=\frac{3g}{4\ell}\sin\theta }
2^\circ 平衡状態の検討（fsolveの利用）
\displaystyle{(1.2a)\quad \theta^*=0}
\displaystyle{(1.2b)\quad \theta^*=\pi}
3^\circ 非線形状態方程式の導出（S-functionの作成）
\displaystyle{(1.3)\quad \frac{d}{dt} \left[\begin{array}{l} \theta \\ \dot{\theta} \end{array}\right] = \left[\begin{array}{l} \dot{\theta} \\ \frac{3g}{4\ell}\sin\theta \end{array}\right] }
4^\circ 非線形シミュレータの開発（平衡状態の保持）
5^\circ 線形化（linmodの利用）
\displaystyle{(1.5)\quad \frac{d}{dt}\left[\begin{array}{c} \theta-\theta^*\\ \dot{\theta} \end{array}\right] = \left[\begin{array}{cc} 0 & 1\\ \frac{3g\cos\theta^*}{4\ell} & 0 \end{array}\right] \left[\begin{array}{cc} \theta-\theta^*\\ \dot{\theta} \end{array}\right] }
6^\circ 線形シミュレータの開発

MAXIMA 
/*pend.wxm*/
dth:'diff(th(t),t);
ddth:'diff(th(t),t,2);
x:ell*sin(th(t));
y:ell*cos(th(t));
J:(1/3)*m*ell^2;
T:(1/2)*m*(diff(x,t)^2+diff(y,t)^2)+(1/2)*J*dth^2;
U:m*g*y;
L:T-U;
LE:diff(diff(L,dth),t)-diff(L,th(t))=0,trigreduce;
sol:solve(LE,ddth);
f:matrix([dth],[rhs(sol[1])]);
a21:diff(f[2,1],th(t)); a22:diff(f[2,1],dth); 
A:matrix([0,1],[a21,a22]);
Simulink 
%sPEND.m
%-----
 function [sys,x0]=sPEND(t,state,input,flag)
%-----
 global g ell th0 
%-----
 if abs(flag)==1
  th=state(1);
  dth=state(2);
  ddth=3*g/(4*ell)*sin(th);
  sys=[dth;ddth];
%-----  
 elseif flag==3
  sys=state;
 elseif flag==0
  sys=[2;0;2;0;0;0];
  x0=[th0;0];
 else
  sys=[];
 end
%-----
%eof
MATLAB 
%lPEND.m
%-----
 clear all, close all
 global mc m ell g th0
 mc=1; m=0.1; ell=0.2; g=9.8;
 th0=0 %input('th(0) = <0,180> ')/180*pi;
%----- 平衡状態の計算
%----- 非線形シミュレータのチェック 
 xs=[th0;0];
 us=[];
 sim("nPEND_obj")
%----- 線形化
 [A0,B0,C0,D0]=linmod('ePEND_linmod',xs,us) 
%
 A=[0 1;0 0];
 A(2,1)=3*g/(4*ell)*cos(th0);
%----- 線形応答と非線形応答の比較
 th0=1/180*pi %input('th(0) = <0,180> ')/180*pi;
 sim("nPEND_comp")  
%-----
%end

[2] CIP
1^\circ 運動方程式の導出（数式処理の利用）
(2.1)\quad \begin{array}{l} \displaystyle{\underbrace{ \left[\begin{array}{ccc} M+m & m\ell\cos\theta \\ m\ell\cos\theta & \frac{4}{3}m\ell^2 \end{array}\right] }_{M(\xi_1)} \underbrace{ \left[\begin{array}{c} \ddot{r} \\ \ddot{\theta} \end{array}\right] }_{\dot{\xi}_2}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 & -m\ell\sin\theta\dot{\theta} \\ 0 & 0 \end{array}\right] }_{C(\xi_1,\xi_2)} \underbrace{ \left[\begin{array}{c} \dot{r} \\ \dot{\theta} \end{array}\right] }_{\dot{\xi}_1}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0\\ -m\ell g\sin\theta \end{array}\right] }_{G(\xi_1)} = \underbrace{ \left[\begin{array}{c} 1 \\ 0 \end{array}\right] F}_{\tilde{F}}} \end{array}
2^\circ 平衡状態の検討（fsolveの利用）
\displaystyle{(2.2a)\quad \theta^*=0}
\displaystyle{(2.2b)\quad \theta^*=\pi}
3^\circ 非線形状態方程式の導出（S-functionの作成）
\displaystyle{(2.3)\quad \frac{d}{dt} \left[\begin{array}{l} \xi_1 \\ \xi_2 \end{array}\right] = \left[\begin{array}{l} \xi_2 \\ M^{-1}(\xi_1)(\tilde{F}-C(\xi_1,\xi_2)\dot{\xi}_1}-G(\xi_1)) \end{array}\right] }
4^\circ 非線形シミュレータの開発（平衡状態の保持）
5^\circ 線形化（linmodの利用）
平衡状態(2.2a)：
\displaystyle{(2.5)\quad \frac{d}{dt}\left[\begin{array}{c} r\\ \theta-\theta^*\\ \dot{r}\\ \dot{\theta} \end{array}\right] = \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & -\frac{3gm}{4M+m} & 0 & 0\\ 0 & \frac{3(M+m)g}{(4M+m)\ell} & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} r\\ \theta-\theta^*\\ \dot{r}\\ \dot{\theta} \end{array}\right] + \left[\begin{array}{c} 0\\ 0\\ \frac{4}{4M+m}\\ \frac{3}{(4M+m)\ell} \end{array}\right] F }
6^\circ 線形シミュレータの開発

MAXIMA 
/*cip.wxm*/
dr:'diff(r(t),t);     ddr:'diff(r(t),t,2);
dth:'diff(th(t),t);   ddth:'diff(th(t),t,2);
x:r(t)+ell*sin(th(t));y:ell*cos(th(t));
J:(1/3)*m*ell^2;
T0:(1/2)*M*dr^2;
T1:(1/2)*m*(diff(x,t)^2+diff(y,t)^2)+(1/2)*J*dth^2;
V1:m*g*y;
L:T0+T1-V1;
LE1:diff(diff(L,dr),t)-diff(L,r(t))=F,trigreduce;
LE2:diff(diff(L,dth),t)-diff(L,th(t))=0,trigreduce;
sol:solve([LE1,LE2],[ddr,ddth]);
f:matrix([dr],[dth],[rhs(sol[1][1])],[rhs(sol[1][2])]);
a31:diff(f[3,1],r(t));a32:diff(f[3,1],th(t));
a33:diff(f[3,1],dr);a34:diff(f[3,1],dth);
a41:diff(f[4,1],r(t));a42:diff(f[4,1],th(t));
a43:diff(f[4,1],dr);a44:diff(f[4,1],dth);
b3:diff(f[3,1],F);b4:diff(f[4,1],F);
A:matrix([0,0,1,0],[0,0,0,1],[a31,a32,a33,a34],[a41,a42,a43,a44]); 
A1:A,th(t)=0; 
A2:A,th(t)=%pi; 
B:matrix([0],[0],[b3],[b4]); 
B1:B,th(t)=0; 
B2:B,th(t)=%pi;
Simulink 
%sCIP.m
%-----
 function [sys,x0]=sCIP(t,state,input,flag)
%-----
 global mc m ell g th0
%-----
 if abs(flag)==1
  F=input(1);
  r=state(1);  th=state(2);
  dr=state(3); dth=state(4);
  cth=cos(th); sth=sin(th);
  M=[mc+m m*ell*cth;
     m*ell*cth 4/3*m*ell^2];
  C=[0 -m*ell*dth*sth;
     0 0];
  G=[ 0;
     -m*ell*g*sth];
  W=M\(-C*[dr;dth]-G+[F;0]);
  ddr=W(1); ddth=W(2);
  sys=[dr;dth;ddr;ddth];
%-----  
 elseif flag==3
  sys=state;
 elseif flag==0
  sys=[4;0;4;1;0;0];
  x0=[0;th0;0;0];
 else
  sys=[];
 end
%-----
%eof
MATLAB 
%lCIP.m
%-----
 clear all, close all
 global mc m ell g th0
 mc=1; m=0.1; ell=0.2; g=9.8;
 th0=0 %input('th(0) = <0,180> ')/180*pi;
%----- 平衡状態の計算
%----- 非線形シミュレータのチェック 
 xs=[0;th0;0;0];
 us=0;
 sim("nCIP_obj")
%----- 線形化
 [A0,B0,C0,D0]=linmod('eCIP_linmod',xs,us) 
%
 A=[zeros(2,2) eye(2);zeros(2,4)];
 A(3,1)=0; 
 A(3,2)=-3*m*g/(m+4*mc); 
 A(4,1)=0; 
 A(4,2)=3*(m+mc)*g/((m+4*mc)*ell);  
 B=zeros(4,1);
 B(3)=4/(m+4*mc);
 B(4)=-3/((m+4*mc)*ell); 
%----- 線形応答と非線形応答の比較
 th0=1/180*pi %input('th(0) = <0,180> ')/180*pi;
 sim("nCIP_comp")  
%-----
%end

[3] CIP2
1^\circ 運動方程式の導出（数式処理の利用）
(3.1)\quad \begin{array}{l} \displaystyle{\underbrace{ \left[\begin{array}{ccc} M+m & m\ell\cos(\theta+\alpha) \\ m\ell\cos(\theta+\alpha) & \frac{4}{3}m\ell^2 \end{array}\right] }_{M(\xi_1)} \underbrace{ \left[\begin{array}{c} \ddot{r} \\ \ddot{\theta} \end{array}\right] }_{\dot{\xi}_2}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 & -m\ell\sin(\theta+\alpha)\dot{\theta} \\ 0 & 0 \end{array}\right] }_{C(\xi_1,\xi_2)} \underbrace{ \left[\begin{array}{c} \dot{r} \\ \dot{\theta} \end{array}\right] }_{\dot{\xi}_1}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} (M+m)g\sin\alpha\\ -m\ell g\sin\theta \end{array}\right] }_{G(\xi_1)} = \left[\begin{array}{c} 1 \\ 0 \end{array}\right] F} \end{array}

2^\circ 平衡状態の検討（fsolveの利用）
\displaystyle{(3.2a)\quad \theta^*=0,\ F^*=(M+m)g\sin\alpha}
\displaystyle{(3.2b)\quad \theta^*=\pi,\ F^*=(M+m)g\sin\alpha}
3^\circ 非線形状態方程式の導出（S-functionの作成）
\displaystyle{(3.3)\quad \frac{d}{dt} \left[\begin{array}{l} \xi_1 \\ \xi_2 \end{array}\right] = \left[\begin{array}{l} \xi_2 \\ M^{-1}(\xi_1)(\tilde{F}-C(\xi_1,\xi_2)\dot{\xi}_1}-G(\xi_1)) \end{array}\right] }
4^\circ 非線形シミュレータの開発（平衡状態の保持）
5^\circ 線形化（linmodの利用）
平衡状態(3.2a)：
(3.5)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} r\\ \theta-\theta^*\\ \dot{r}\\ \dot{\theta} \end{array}\right] = \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & -\frac{6\cos\alpha mg}{8M+(5-3\cos2\alpha)m} & 0 & 0\\ 0 & \frac{6(M+m)g}{(8M+(5-3\cos2\alpha)m)\ell} & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} r\\ \theta-\theta^*\\ \dot{r}\\ \dot{\theta} \end{array}\right]}\\ \displaystyle{+ \left[\begin{array}{c} 0\\ 0\\ \frac{8}{8M+(5-3\cos2\alpha)m}\\ \frac{6\cos\alpha}{(8M+(5-3\cos2\alpha)m)\ell} \end{array}\right] (F-F^*)} \end{array}
6^\circ 線形シミュレータの開発

MAXIMA 
/*cip2.wxm*/
dr:'diff(r(t),t); ddr:'diff(r(t),t,2);
dth:'diff(th(t),t); ddth:'diff(th(t),t,2);
x0:r(t)*cos(alpha); y0:r(t)*sin(alpha);
T0:(1/2)*M*(diff(x0,t)^2+diff(y0,t)^2); 
V0:M*g*y0;
x1:x0+ell*sin(th(t)); y1:y0+ell*cos(th(t));
J1:(1/3)*m*ell^2;
T1:(1/2)*m*(diff(x1,t)^2+diff(y1,t)^2)+(1/2)*J1*dth^2;
V1:m*g*y1;
L:T0+T1-V0-V1;
LE1:diff(diff(L,dr),t)-diff(L,r(t))=F,trigreduce,ratsimp;
LE2:diff(diff(L,dth),t)-diff(L,th(t))=0,trigreduce,ratsimp;
sol:solve([LE1,LE2],[ddr,ddth]);
f:matrix([dr],[dth],[rhs(sol[1][1])],[rhs(sol[1][2])]);
a31:diff(f[3,1],r(t));a32:diff(f[3,1],th(t));
a33:diff(f[3,1],dr);a34:diff(f[3,1],dth);
a41:diff(f[4,1],r(t));a42:diff(f[4,1],th(t));
a43:diff(f[4,1],dr);a44:diff(f[4,1],dth);
b3:diff(f[3,1],F);b4:diff(f[4,1],F);
A:matrix([0,0,1,0],[0,0,0,1],[a31,a32,a33,a34],
[a41,a42,a43,a44]); 
A1:A,th(t)=0,F=(M+m)*g*sin(alpha),trigreduce,ratsimp; 
A2:A,th(t)=%pi,F=(M+m)*g*sin(alpha),trigreduce,ratsimp; 
B:matrix([0],[0],[b3],[b4]); 
B1:B,th(t)=0,F=(M+m)*g*sin(alpha),trigreduce,ratsimp; 
B2:B,th(t)=%pi,F=(M+m)*g*sin(alpha),trigreduce,ratsimp;
Simulink 
%sCIP2.m
%-----
 function [sys,x0]=sCIP2(t,state,input,flag)
%-----
 global mc m ell g alpha th0
%-----
 if abs(flag)==1
  F=input(1);
  r=state(1);  th=state(2);
  dr=state(3); dth=state(4);
  mc=1; m=0.1; ell=0.2; g=9.8;
  M=[mc+m m*ell*cos(th+alpha);
     m*ell*cos(th+alpha) 4/3*m*ell^2];
  C=[0 -m*ell*dth*sin(th+alpha);
     0 0];
  G=[(mc+m)*g*sin(alpha);
     -m*ell*g*sin(th)];
  W=M\(-C*[dr;dth]-G+[F;0]);
  ddr=W(1); ddth=W(2);
  sys=[dr;dth;ddr;ddth];
%-----  
 elseif flag==3
  sys=state;
 elseif flag==0
  sys=[4;0;4;1;0;0];
  x0=[0;th0;0;0];
 else
  sys=[];
 end
%-----
%eof
MATLAB 
%lCIP2.m
%-----
 clear all, close all
 global mc m ell g alpha th0
 mc=1; m=0.1; ell=0.2; g=9.8;
 alpha=3/180*pi;
 th0=0 %input('ths   = <0,180> ')/180*pi;
%----- 平衡状態の計算
%----- 非線形シミュレータのチェック 
 xs=[0;th0;0;0];
 us=(mc+m)*g*sin(alpha);
 sim("nCIP2_obj")
%----- 線形化
 [A0,B0,C0,D0]=linmod('eCIP2_linmod',xs,us) 
%
 A=[zeros(2,2) eye(2);zeros(2,4)];
 A(3,1)=0; 
 A(3,2)=-6*cos(alpha)*m*g/(8*mc+(5-3*cos(2*alpha))*m); 
 A(4,1)=0; 
 A(4,2)=6*(m+mc)*g/((8*mc+(5-3*cos(2*alpha))*m)*ell);  
 B=zeros(4,1);
 B(3)=8/(8*mc+(5-3*cos(2*alpha))*m);
 B(4)=-6*cos(alpha)/((8*mc+(5-3*cos(2*alpha))*m)*ell); 
%----- 線形応答と非線形応答の比較
 th0=1/180*pi %input('th(0) = <0,180> ')/180*pi;
 CM=[100      0 0 0; 
       0 180/pi 0 0]
 sim("nCIP2_comp")  
%-----
%end

[4] AIP
1^\circ 運動方程式の導出（数式処理の利用）
(4.1)\quad \begin{array}{l} \displaystyle{\underbrace{ \left[\begin{array}{ccc} (\frac{4}{3}m_1+4m_2)\ell_1^2 & 2m_2\ell_1\ell_2\cos(\theta_2-\theta_1)\\ 2m_2\ell_1\ell_2\cos(\theta_2-\theta_1) & \frac{4}{3}m_2\ell_2^2 \end{array}\right] }_{M(\xi_1)} \underbrace{ \left[\begin{array}{c} \ddot{\theta}_1 \\ \ddot{\theta}_2 \end{array}\right] }_{\dot{\xi}_2}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 & -2m_2\ell_1\ell_2\sin(\theta_2-\theta_1) \dot{\theta}_2\\ 2m_2\ell_1\ell_2\sin(\theta_2-\theta_1) \dot{\theta}_1 & 0\\ \end{array}\right] }_{C(\xi_1,\xi_2)} \underbrace{ \left[\begin{array}{c} \dot{\theta}_1 \\ \dot{\theta}_2 \end{array}\right] }_{\dot{\xi}_1}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} -(m_1+2m_2)\ell_1g\sin\theta_1\\ -m_2\ell_2g\sin\theta_2 \end{array}\right] }_{G(\xi_1)} = \underbrace{ \left[\begin{array}{c} 1 \\ 0 \end{array}\right] \tau}_{\tilde{\tau}}} \end{array}
2^\circ 平衡状態の検討（fsolveの利用）
\displaystyle{(4.2a)\quad \theta_1^*\ne 0,\ \theta_2^*=0,\ \tau^*=-(m_1+2m_2)\ell_1g\sin\theta_1^*}
\displaystyle{(4.2b)\quad \theta_1^*\ne 0,\ \theta_2^*=\pi,\ \tau^*=-(m_1+2m_2)\ell_1g\sin\theta_1^*}
3^\circ 非線形状態方程式の導出（S-functionの作成）
\displaystyle{(4.3)\quad \frac{d}{dt} \left[\begin{array}{l} \xi_1 \\ \xi_2 \end{array}\right] = \left[\begin{array}{l} \xi_2 \\ M^{-1}(\xi_1)(\tilde{\tau}-C(\xi_1,\xi_2)\dot{\xi}_1}-G(\xi_1)) \end{array}\right] }
4^\circ 非線形シミュレータの開発（平衡状態の保持）
5^\circ 線形化（linmodの利用）
・\theta_1^*=0の場合の平衡状態(4.2a)：
(4.5a)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right] =}\\ \displaystyle{\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \frac{3(m_1+2m_2)g}{(4m_1+3m_2)\ell_1} & -\frac{9m_2g}{2(4m_1+3m_2)\ell_1} & 0 & 0\\ -\frac{9(m_1+2m_2)g}{2(4m_1+3m_2)\ell_1} & \frac{9m_2g}{(4m_1+3m_2)\ell_2} & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right]}\\ \displaystyle{+ \left[\begin{array}{c} 0\\ 0\\ \frac{6}{2(4m_1+3m_2)\ell_1^2}\\ -\frac{9}{2(4m_1+3m_2)\ell_1\ell_2} \end{array}\right] (\tau-\tau^*)} \end{array}
・\theta_1^*=\alphaの場合の平衡状態(4.2a)：
(4.5b)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right] =}\\ \displaystyle{\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ a_{31}(\alpha) & a_{32}(\alpha) & 0 & 0\\ a_{41}(\alpha) & a_{42}(\alpha) & 0 & 0 \end{array}\right] \left[\begin{array}{c} \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right]}\\ \displaystyle{+ \left[\begin{array}{c} 0\\ 0\\ \frac{6}{2(4m_1+3(4-3\cos^2\alpha)m_2)\ell_1^2}\\ -\frac{6}{2(4m_1+3(4-3\cos^2\alpha)m_2)\ell_1\ell_2} \end{array}\right] (\tau-\tau^*)} \end{array}

6^\circ 線形シミュレータの開発

MAXIMA 
/*aip.wxm*/
dth1:'diff(th1(t),t);     ddth1:'diff(th1(t),t,2);
dth2:'diff(th2(t),t);     ddth2:'diff(th2(t),t,2);
x1:ell1*sin(th1(t));      y1:ell1*cos(th1(t));
x2:2*x1+ell2*sin(th2(t)); y2:2*y1+ell2*cos(th2(t));
J1:(1/3)*m1*ell1^2;       J2:(1/3)*m2*ell2^2;
T1:(1/2)*m1*(diff(x1,t)^2+diff(y1,t)^2)+(1/2)*J1*dth1^2;
T2:(1/2)*m2*(diff(x2,t)^2+diff(y2,t)^2)+(1/2)*J2*dth2^2;
V1:m1*g*y1; V2:m2*g*y2;
L:T1+T2-V1-V2;
LE1:diff(diff(L,dth1),t)-diff(L,th1(t))=tau,trigreduce,ratsimp;
LE2:diff(diff(L,dth2),t)-diff(L,th2(t))=0,trigreduce,ratsimp;
sol:solve([LE1,LE2],[ddth1,ddth2]);
f:matrix([dth1],[dth2],[rhs(sol[1][1])],[rhs(sol[1][2])]);
a31:diff(f[3,1],th1(t));  a32:diff(f[3,1],th2(t));
a33:diff(f[3,1],dth1);    a34:diff(f[3,1],dth2);
a41:diff(f[4,1],th1(t));  a42:diff(f[4,1],th2(t));
a43:diff(f[4,1],dth1);    a44:diff(f[4,1],dth2);
b3:diff(f[3,1],tau);      b4:diff(f[4,1],tau);
A:matrix([0,0,1,0],[0,0,0,1],
[a31,a32,a33,a34],[a41,a42,a43,a44]); 
A1:A,th1(t)=0,th2(t)=0,dth1=0,dth2=0,tau=(m1+2*m2)*ell1*g*sin(th1(t)),ratsimp; 
A2:A,th1(t)=%pi,th2(t)=0,dth1=0,dth2=0,tau=-(m1+2*m2)*ell1*g*sin(th1(t)),ratsimp;
A3:A,th1(t)=alpha,th2(t)=0,dth1=0,dth2=0,tau=(m1+2*m2)*ell1*g*sin(alpha),'diff(alpha,t)=0;ratsimp;
B:matrix([0],[0],[b3],[b4]); 
B1:B,th1(t)=0,th2(t)=0,dth1=0,dth2=0,tau=-(m1+2*m2)*ell1*g*sin(th1(t)),simplify; 
B2:B,th1(t)=%pi,th2(t)=0,dth1=0,dth2=0,tau=(m1+2*m2)*ell1*g*sin(th1(t)),simplify; 
B3:B,th1(t)=alpha,th2(t)=0,dth1=0,dth2=0,tau=-(m1+2*m2)*ell1*g*sin(alpha),simplify;
Simulink 
%sAIP.m
%-----
 function [sys,x0]=sAIP(t,state,input,flag)
%-----
 global m1 m2 ell1 ell2 g th10 th20
%-----
 if abs(flag)==1
  tau=input(1);
  th1=state(1);  th2=state(2);
  dth1=state(3); dth2=state(4);
  cth1=cos(th1); sth1=sin(th1);
  cth2=cos(th2); sth2=sin(th2);
  cth21=cos(th2-th1); sth21=sin(th2-th1);
  M=[4/3*m1*ell1^2+4*m2*ell1^2, 2*m2*ell1*ell2*cth21;
     2*m2*ell1*ell2*cth21 4/3*m2*ell2^2];
  C=[0 -2*m2*ell1*ell2*dth2*sth21;
     2*m2*ell1*ell2*dth1*sth21 0];
  G=[-(m1+2*m2)*ell1*g*sth1;
     -m2*ell2*g*sth2];
  W=M\(-C*[dth1;dth2]-G+[tau;0]);
  ddth1=W(1); ddth2=W(2);
  sys=[dth1;dth2;ddth1;ddth2];
%-----  
 elseif flag==3
  sys=state;
 elseif flag==0
  sys=[4;0;4;1;0;0];
  x0=[th10;th20;0;0];
 else
  sys=[];
 end
%-----
%eof
MATLAB 
%lAIP.m
%-----
 clear all, close all
 global m1 m2 ell1 ell2  g th10 th20
 m1=0.1; m2=0.2; ell1=0.1; ell2=0.2; g=9.8;
 th10=0 %input('th1(0) = <0,180> ')/180*pi;
 th20=0 %input('th2(0) = <0,180> ')/180*pi;  
%----- 平衡状態の計算
%----- 非線形シミュレータのチェック 
 xs=[th10;th20;0;0];
 us=-(m1+2*m2)*ell1*g*sin(th10)
 sim("nAIP_obj")  
%----- 線形化
 [A0,B0,C0,D0]=linmod('eAIP_linmod',xs,us) 
%
 A=[zeros(2,2) eye(2);zeros(2,4)];
 A(3,1)=3*(2*m2+m1)*g/((3*m2+4*m1)*ell1); 
 A(3,2)=-9*m2*g/(2*(3*m2+4*m1)*ell1); 
 A(4,1)=-9*(2*m2+m1)*g/(2*(3*m2+4*m1)*ell2); 
 A(4,2)=3*(3*m2+m1)*g/((3*m2+4*m1)*ell2);  
 B=zeros(4,1);
 B(3)=3/((3*m2+4*m1)*ell1^2);
 B(4)=-9/(2*(3*m2+4*m1)*ell1*ell2);
%----- 線形応答と非線形応答の比較
 th20=1/180*pi %input('th(0) = <0,180> ')/180*pi;
 CM=[180/pi      0 0 0; 
       0    180/pi 0 0]
 sim("nAIP_comp")  
%-----
%end

[5] PIP
1^\circ 運動方程式の導出（数式処理の利用）
(5.1)\quad \begin{array}{l} \displaystyle{\underbrace{ \left[\begin{array}{ccc} M+m_1+m_2 & (m_1+2m_2)\ell_1\cos\theta_1 & m_2\ell_2\cos\theta_2\\ (m_1+2m_2)\ell_1\cos\theta_1 & (\frac{4}{3}m_1+4m_2)\ell_1^2 & 2m_2\ell_1\ell_2\cos(\theta_2-\theta_1)\\ m_2\ell_2\cos\theta_2 & 2m_2\ell_1\ell_2\cos(\theta_2-\theta_1) & \frac{4}{3}m_2\ell_2^2 \end{array}\right] }_{M(\xi_1)} \underbrace{ \left[\begin{array}{c} \ddot{r} \\ \ddot{\theta}_1 \\ \ddot{\theta}_2 \end{array}\right] }_{\dot{\xi}_2}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 & -(m_1+2m_2)\ell_2\sin\theta_2 \dot{\theta}_1 & -m_2\ell_2\sin\theta_2 \dot{\theta}_2\\ 0 & 0 & 2m_2\ell_1\ell_2\sin(\theta_2-\theta_1) \dot{\theta}_2\\ 0 & 2m_2\ell_1\ell_2\sin(\theta_2-\theta_1) \dot{\theta}_1 & 0\\ \end{array}\right] }_{C(\xi_1,\xi_2)} \underbrace{ \left[\begin{array}{c} \dot{r} \\ \dot{\theta}_1 \\ \dot{\theta}_2 \end{array}\right] }_{\dot{\xi}_1}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 \\ (m_1+3m_2)\ell_1g\sin\theta_1\\ -m_2\ell_2g\sin\theta_2 \end{array}\right] }_{G(\xi_1)} = \underbrace{ \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] F}_{\tilde{F}} \end{array}
2^\circ 平衡状態の検討（fsolveの利用）
\displaystyle{(5.2)\quad \theta_1^*=0,\ \theta_2^*=0 }
3^\circ 非線形状態方程式の導出（S-functionの作成）
\displaystyle{(5.3)\quad \frac{d}{dt} \left[\begin{array}{l} \xi_1 \\ \xi_2 \end{array}\right] = \left[\begin{array}{l} \xi_2 \\ M^{-1}(\xi_1)(\tilde{F}-C(\xi_1,\xi_2)\dot{\xi}_1}-G(\xi_1)) \end{array}\right] }
4^\circ 非線形シミュレータの開発（平衡状態の保持）
5^\circ 線形化（linmodの利用）
平衡状態(5.2)：
(5.5)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} r\\ \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{r}\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right] =}\\ \displaystyle{\left[\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ 0 & -\frac{3m_1g}{4M+m_1+m_2} & -\frac{3m_2g}{4M+m_1+m_2} & 0 & 0 & 0\\ 0 & \frac{3(4m+4m_1+m_2)g}{4(4M+m_1+m_2)\ell_1} & \frac{9m_2g}{4(4M+m_1+m_2)\ell_1} & 0 & 0& 0\\ 0 & \frac{9gm_1}{4(4M+m_1+m_2)\ell_2} & \frac{3(4m+m_1+4m_2)g}{4(4M+m_1+m_2)\ell_2} & 0 & 0& 0\\ \end{array}\right] \left[\begin{array}{c} r\\ \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{r}\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right]}\\ \displaystyle{+ \left[\begin{array}{c} 0\\ 0\\ 0\\ \frac{4}{4M+m_1+m_2}\\ -\frac{3}{(4M+m_1+m_2)\ell_1}\\ -\frac{3}{(4M+m_1+m_2)\ell_2} \end{array}\right] F \end{array}
6^\circ 線形シミュレータの開発

MAXIMA 
/*pip.wxm*/
dr:'diff(r(t),t);         ddr:'diff(r(t),t,2);
dth1:'diff(th1(t),t);     ddth1:'diff(th1(t),t,2);
dth2:'diff(th2(t),t);     ddth2:'diff(th2(t),t,2);
x1:r(t)+ell1*sin(th1(t)); y1:ell1*cos(th1(t));
x2:r(t)+ell2*sin(th2(t)); y2:ell2*cos(th2(t));
J1:(1/3)*m1*ell1^2;       J2:(1/3)*m2*ell2^2;
T0:(1/2)*M*dr^2;
T1:(1/2)*m1*(diff(x1,t)^2+diff(y1,t)^2)+(1/2)*J1*dth1^2;
T2:(1/2)*m2*(diff(x2,t)^2+diff(y2,t)^2)+(1/2)*J2*dth2^2;
V1:m1*g*y1; V2:m2*g*y2;
L:T0+T1+T2-V1-V2;
LE0:diff(diff(L,dr),t)-diff(L,r(t))=F,trigreduce;
LE1:diff(diff(L,dth1),t)-diff(L,th1(t))=0,trigreduce;
LE2:diff(diff(L,dth2),t)-diff(L,th2(t))=0,trigreduce;
sol:solve([LE0,LE1,LE2],[ddr,ddth1,ddth2]);
f:matrix([dr],[dth1],[dth2],
[rhs(sol[1][1])],[rhs(sol[1][2])],[rhs(sol[1][3])]);
a41:diff(f[4,1],r(t));    a42:diff(f[4,1],th1(t));
a43:diff(f[4,1],th2(t));  a44:diff(f[4,1],dr);
a45:diff(f[4,1],dth1);    a46:diff(f[4,1],dth2);
a51:diff(f[5,1],r(t));    a52:diff(f[5,1],th1(t));
a53:diff(f[5,1],th2(t));  a54:diff(f[5,1],dr);
a55:diff(f[5,1],dth1);    a56:diff(f[5,1],dth2);
a61:diff(f[6,1],r(t));    a62:diff(f[6,1],th1(t));
a63:diff(f[6,1],th2(t));  a64:diff(f[6,1],dr);
a65:diff(f[6,1],dth1);    a66:diff(f[6,1],dth2);
b4:diff(f[4,1],F);b5:diff(f[5,1],F); b6:diff(f[6,1],F);
A:matrix([0,0,0,1,0,0],[0,0,0,0,1,0],[0,0,0,0,0,1],
[a41,a42,a43,a44,a45,a46],[a51,a52,a53,a54,a55,a56],
[a61,a62,a63,a64,a65,a66]); 
A1:A,r(t)=0,th1(t)=0,th2(t)=0,dr=0,dth1=0,dth2=0,F=0,ratsimp;
B:matrix([0],[0],[0],[b4],[b5],[b6]); 
B1:B,r(t)=0,th1(t)=0,th2(t)=0,dr=0,dth1=0,dth2=0,F=0,ratsimp;
Simulink 
%sPIP.m
%-----
 function [sys,x0]=sPIP(t,state,input,flag)
%-----
 global mc m1 m2 ell1 ell2 g th10 th20
%-----
 if abs(flag)==1
  F=input(1);
  r=state(1);  th1=state(2); th2=state(3);  
  dr=state(4);  dth1=state(5); dth2=state(6);  
  cth1=cos(th1); sth1=sin(th1);
  cth2=cos(th2); sth2=sin(th2);
  M=[mc+m1+m2 m1*ell1*cth1 m2*ell2*cth2;
     m1*ell1*cth1 4/3*m1*ell1^2 0;
     m2*ell2*cth2 0 4/3*m2*ell2^2];
  C=[0 -m1*ell1*dth1*sth1 -m2*ell2*dth2*sth2;
     0 0 0;
     0 0 0];
  G=[ 0;
     -m1*ell1*g*sth1
     -m2*ell2*g*sth2];
  W=M\(-C*[dr;dth1;dth2]-G+[F;0;0]);
  ddr=W(1); ddth1=W(2); ddth2=W(3);
  sys=[dr;dth1;dth2;ddr;ddth1;ddth2];
%-----  
 elseif flag==3
  sys=state;
 elseif flag==0
  sys=[6;0;6;1;0;0];
  x0=[0;th10;th20;0;0;0];
 else
  sys=[];
 end
%-----
%eof
MATLAB 
%lPIP.m
%-----
 clear all, close all
 global mc m1 m2 ell1 ell2 g th10 th20
 mc=1; m1=0.1; m2=0.2; ell1=0.15; ell2=0.2; g=9.8;
 th10=0 %input('th1(0) = <0,180> ')/180*pi;
 th20=0 %input('th2(0) = <0,180> ')/180*pi;  
%----- 平衡状態の計算
%----- 非線形シミュレータのチェック 
 xs=[0;th10;th20;0;0;0];
 us=0;
 sim("nPIP_obj")  
%----- 線形化
 [A0,B0,C0,D0]=linmod('ePIP_linmod',xs,us) 
%
 A=[zeros(3,3) eye(3);zeros(3,6)];
 A(4,1)=0; 
 A(4,2)=-3*m1*g/(m1+m2+4*mc); 
 A(4,3)=-3*m2*g/(m1+m2+4*mc);  
 A(5,1)=0; 
 A(5,2)=(12*m1+3*m2+12*mc)*g/((4*m1+4*m2+16*mc)*ell1);  
 A(5,3)=9*m2*g/((4*m1+4*m2+16*mc)*ell1);   
 A(6,1)=0; 
 A(6,2)=9*m1*g/((4*m1+4*m2+16*mc)*ell2);  
 A(6,3)=(3*m1+12*m2+12*mc)*g/((4*m1+4*m2+16*mc)*ell2);   
 B=zeros(6,1);
 B(4)=4/(m1+m2+4*mc);
 B(5)=-3/((m1+m2+4*mc)*ell1);
 B(6)=-3/((m1+m2+4*mc)*ell2); 
%----- 線形応答と非線形応答の比較
 th10=1/180*pi %input('th(0) = <0,180> ')/180*pi;
 th20=-1/180*pi %input('th(0) = <0,180> ')/180*pi;
 CM=[diag([100,180/pi,180/pi]),zeros(3,3)];
 sim("nPIP_comp")  
%-----
%end

[6] DIP
1^\circ 運動方程式の導出（数式処理の利用）
(6.1)\quad \begin{array}{l} \displaystyle{\underbrace{ \left[\begin{array}{ccc} M+m_1+m_2 & m_1\ell_1\cos\theta_1 & -m_2\ell_2\cos\theta_2\\ m_1\ell_1\cos\theta_1 & \frac{4}{3}m_1\ell_1^2 & 0\\ -m_2\ell_2\cos\theta_2 & 0 & \frac{4}{3}m_2\ell_2^2 \end{array}\right] }_{M(\xi_1)} \underbrace{ \left[\begin{array}{c} \ddot{r} \\ \ddot{\theta}_1 \\ \ddot{\theta}_2 \end{array}\right] }_{\dot{\xi}_2}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 & -m_1\ell_2\sin\theta_2 \dot{\theta}_1 & -m_2\ell_2\sin\theta_2 \dot{\theta}_2\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{array}\right] }_{C(\xi_1,\xi_2)} \underbrace{ \left[\begin{array}{c} \dot{r} \\ \dot{\theta}_1 \\ \dot{\theta}_2 \end{array}\right] }_{\dot{\xi}_1}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 \\ -m_1\ell_1g\sin\theta_1\\ -m_2\ell_2g\sin\theta_2 \end{array}\right] }_{G(\xi_1)} = \underbrace{ \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] F}_{\tilde{F}} \end{array}
2^\circ 平衡状態の検討（fsolveの利用）
\displaystyle{(6.2)\quad \theta_1^*=0,\ \theta_2^*=0 }
3^\circ 非線形状態方程式の導出（S-functionの作成）
\displaystyle{(6.3)\quad \frac{d}{dt} \left[\begin{array}{l} \xi_1 \\ \xi_2 \end{array}\right] = \left[\begin{array}{l} \xi_2 \\ M^{-1}(\xi_1)(\tilde{F}-C(\xi_1,\xi_2)\dot{\xi}_1}-G(\xi_1)) \end{array}\right] }
4^\circ 非線形シミュレータの開発（平衡状態の保持）
5^\circ 線形化（linmodの利用）
平衡状態(6.2)：
(6.5)\quad \begin{array}{l} \displaystyle{ \frac{d}{dt}\left[\begin{array}{c} r\\ \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{r}\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right] =}\\ \displaystyle{ \left[\begin{array}{cccccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & -\frac{3m_1g}{Mm_1+m_1^2+(3M+m1)m_2} & -\frac{3m_2g}{Mm_1+m_1^2+(3M+m1)m_2} \\ 0 & \frac{3(4Mm_1+4m_1^2+3m_2^2+3(18M+13m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m1)m_2)\ell_1} & \frac{9(2M+m_1)m_2g}{(4Mm_1+m_1^2+(3M+m1)m_2)\ell_1} \\ 0 & \frac{9(2Mm_1+m_1^2+3(2M+m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} & \frac{3(4Mm_1+m_1^2+12(3M+m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} \\ \end{array}\right.}\\ \displaystyle{\left.\begin{array}{cccccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} r\\ \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{r}\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right]}\\ \displaystyle{+ \left[\begin{array}{c} 0\\ 0\\ 0\\ \frac{4m_1+3m_2}{4Mm_1+m_1^2+(3M+m1)m_2}\\ -\frac{3(2m_1+m2)}{2Mm_1+m_1^2+(3M+m1)m_2}\\ \frac{3m_1}{2(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} \end{array}\right] F} \end{array}

6^\circ 線形シミュレータの開発

MAXIMA 
/*dip.wxm*/
dr:'diff(r(t),t);         ddr:'diff(r(t),t,2);
dth1:'diff(th1(t),t);     ddth1:'diff(th1(t),t,2);
dth2:'diff(th2(t),t);     ddth2:'diff(th2(t),t,2);
x1:r(t)+ell1*sin(th1(t)); y1:ell1*cos(th1(t));
x2:r(t)+2*ell1*sin(th1(t))+ell2*sin(th2(t)); 
y2:2*y1+ell2*cos(th2(t));
J1:(1/3)*m1*ell1^2;       J2:(1/3)*m2*ell2^2;
T0:(1/2)*M*dr^2;
T1:(1/2)*m1*(diff(x1,t)^2+diff(y1,t)^2)+(1/2)*J1*dth1^2;
T2:(1/2)*m2*(diff(x2,t)^2+diff(y2,t)^2)+(1/2)*J2*dth2^2;
V1:m1*g*y1; V2:m2*g*(y1+y2);
L:T0+T1+T2-V1-V2;
LE0:diff(diff(L,dr),t)-diff(L,r(t))=F,trigreduce;
LE1:diff(diff(L,dth1),t)-diff(L,th1(t))=0,trigreduce;
LE2:diff(diff(L,dth2),t)-diff(L,th2(t))=0,trigreduce;
sol:solve([LE0,LE1,LE2],[ddr,ddth1,ddth2]);
f:matrix([dr],[dth1],[dth2],
[rhs(sol[1][1])],[rhs(sol[1][2])],[rhs(sol[1][3])]);
a41:diff(f[4,1],r(t));    a42:diff(f[4,1],th1(t));
a43:diff(f[4,1],th2(t));  a44:diff(f[4,1],dr);
a45:diff(f[4,1],dth1);    a46:diff(f[4,1],dth2);
a51:diff(f[5,1],r(t));    a52:diff(f[5,1],th1(t));
a53:diff(f[5,1],th2(t));  a54:diff(f[5,1],dr);
a55:diff(f[5,1],dth1);    a56:diff(f[5,1],dth2);
a61:diff(f[6,1],r(t));    a62:diff(f[6,1],th1(t));
a63:diff(f[6,1],th2(t));  a64:diff(f[6,1],dr);
a65:diff(f[6,1],dth1);    a66:diff(f[6,1],dth2);
b4:diff(f[4,1],F);b5:diff(f[5,1],F); b6:diff(f[6,1],F);
A:matrix([0,0,0,1,0,0],[0,0,0,0,1,0],[0,0,0,0,0,1],
[a41,a42,a43,a44,a45,a46],[a51,a52,a53,a54,a55,a56],
[a61,a62,a63,a64,a65,a66]); 
A1:A,r(t)=0,th1(t)=0,th2(t)=0,dr=0,dth1=0,dth2=0,F=0,
ell1=ell,ell2=ell,ratsimp;
B:matrix([0],[0],[0],[b4],[b5],[b6]); 
B1:B,r(t)=0,th1(t)=0,th2(t)=0,dr=0,dth1=0,dth2=0,F=0,
ell1=ell,ell2=ell,ratsimp;
Simulink 
%sDIP.m
%-----
 function [sys,x0]=sDIP(t,state,input,flag)
%-----
 global mc m1 m2 ell1 ell2 g th10 th20
%-----
 if abs(flag)==1
  F=input(1);
  r=state(1);  th1=state(2); th2=state(3);  
  dr=state(4);  dth1=state(5); dth2=state(6);  
  cth1=cos(th1); sth1=sin(th1);
  cth2=cos(th2); sth2=sin(th2);
  cth21=cos(th2-th1); sth21=sin(th2-th1); 
  M=[mc+m1+m2 (m1+2*m2)*ell1*cth1 m2*ell2*cth2;
     (m1+2*m2)*ell1*cth1 (4/3*m1+4*m2)*ell1^2 2*m2*ell1*ell2*cth21;
     m2*ell2*cth2 2*m2*ell1*ell2*cth21 4/3*m2*ell2^2];
  C=[0 -(m1+2*m2)*ell1*sth1*dth1 -m2*ell2*sth2*dth2;
     0 0 2*m2*ell1*ell2*cth21*dth2;
     0 2*m2*ell1*ell2*cth21*dth1 0];
  G=[ 0;
     -(m1+3*m2)*ell1*g*sth1
     -m2*ell2*g*sth2];
  W=M\(-C*[dr;dth1;dth2]-G+[F;0;0]);
  ddr=W(1); ddth1=W(2); ddth2=W(3);
  sys=[dr;dth1;dth2;ddr;ddth1;ddth2];
%-----  
 elseif flag==3
  sys=state;
 elseif flag==0
  sys=[6;0;6;1;0;0];
  x0=[0;th10;th20;0;0;0];
 else
  sys=[];
 end
%-----
%eof
MATLAB 
%lDIP.m
%-----
 clear all, close all
 global mc m1 m2 ell1 ell2 g th10 th20
 mc=1; m=0.1; m1=m; m2=m; ell=0.15; ell1=ell; ell2=ell; g=9.8;
 th10=0 %input('th1(0) = <0,180> ')/180*pi;
 th20=0 %input('th2(0) = <0,180> ')/180*pi;  
%----- 平衡状態の計算
%----- 非線形シミュレータのチェック 
 xs=[0;th10;th20;0;0;0];
 us=0;
 sim("nDIP_obj")  
%----- 線形化
 [A0,B0,C0,D0]=linmod('eDIP_linmod',xs,us) 
%
 A=[zeros(3,3) eye(3);zeros(3,6)];
 A(4,1)=0; 
 A(4,2)=-18*m*g/(2*m+7*mc); 
 A(4,3)=3*m*g/(4*m+14*mc);  
 A(5,1)=0; 
 A(5,2)=(15*m+12*mc)*g/((2*m+7*mc)*ell);  
 A(5,3)=-(9*m+18*mc)*g/((8*m+28*mc)*ell);   
 A(6,1)=0; 
 A(6,2)=-(9*m+18*mc)*g/((2*m+7*mc)*ell);  
 A(6,3)=(15*m+48*mc)*g/((8*m+28*mc)*ell);   
 B=zeros(6,1);
 B(4)=7/(2*m+7*mc);
 B(5)=-9/((4*m+14*mc)*ell);
 B(6)=3/((4*m+14*mc)*ell);
%----- 線形応答と非線形応答の比較
 th10=1/180*pi %input('th(0) = <0,180> ')/180*pi;
 th20=-1/180*pi %input('th(0) = <0,180> ')/180*pi;
 CM=[diag([100,180/pi,180/pi]),zeros(3,3)];
 sim("nDIP_comp")  
%-----
%end