浮体制御(非公開)

長崎大学・西松建設間共同研究
「洋上風車工事用浮体安定化制御」
長崎大学海洋未来イノベーション機構・特定教授, 九州大学名誉教授経塚雄策
西松建設（株）技術研究所, 長崎大学海洋未来イノベーション機構・連携研究員高村浩彰
元九州大学准教授　中村昌彦（協力者）
九州大学名誉教授　梶原宏之（協力者）

1.はじめに

波浪中浮体の制御方式として
LQ制御/H∞制御
LQ-IM制御/H∞-IM制御
SM制御
の５通りを考え
非線形シミュレーション
により比較検討を行った。

2.モデリング
2.1 運動方程式
$[a_{i^*j^*}]\underbrace{\left[\begin{array}{c}\dot{w}\\\dot{p}\\\dot{q}\end{array}\right]}_{\dot{\vec\nu}} +[b_{i^*j^*}]\underbrace{\left[\begin{array}{c}w\\p\\q\end{array}\right]}_{\vec\nu} +[c_{i^*j^*}]\underbrace{\left[\begin{array}{c}z\\\phi\\\theta\\\end{array}\right]}_{\vec\eta}= [f_{i^*k}]\underbrace{\left[\begin{array}{c}F_z\\F_\phi\\F_\theta\end{array}\right]}_{\vec\tau}$
$+\underbrace{[g_{i^*\beta}]H_w\cos\frac{2\pi}{T_w} t}_{F_C}-\underbrace{[h_{i^*\beta}]H_w\sin\frac{2\pi}{T_w} t}_{F_S}$

浮体の運動方程式は付録に示すように元々６自由度であるが、ヒーブ、ロール、ピッチの３自由度だけを取り出したのが上式である(実機ではDPSにより、実験では係留策によりサージ、スウェイ、ヨーは拘束される)。ただし、 $[a_{ij}]$ などは要素 $a_{ij}$ をもつ行列を表し、 $i^*,j^*=3,4,5$ 、 $k=1,2,3$ 、 $\beta=45,90^\circ$ 、 $[f_{i^*\kappa}]=\frac{9.8}{1000} \left[\begin{array}{ccc}1 & 0 & 0\\0 & 0.365 & 0\\0 & 0 & 0.63\end{array}\right]$ 、 $H_w$ は波高、 $T_w$ は波周期。また $F_z,F_\phi,F_\theta$ はそれぞれヒーブ駆動力、ロール駆動モーメント、ピッチ駆動モーメント。 $F_C$ は静水圧や付加質量と同位相の波浪外力、 $F_S$ は減衰力と同位相の波浪外力。

2.2 状態方程式
$\underbrace{\frac{d}{dt}\left[\begin{array}{c}z\\\phi\\\theta\\\hline w\\p\\q\\\end{array}\right]}_{\dot{\vec x}}= \underbrace{\left[\begin{array}{cc}0_{3\times3} & R(\phi,\theta,0)\\-[a_{i^*j^*}]^{-1}[c_{i^*j^*}] & -[a_{i^*j^*}]^{-1}[b_{i^*j^*}] \end{array}\right]}_{A} \underbrace{\left[\begin{array}{c}z\\\phi\\\theta\\\hline w\\p\\q\\\end{array}\right]}_{\vec x}$
$+\underbrace{\left[\begin{array}{c} 0_{3\times3} \\ \left[a_{i^*j^*}\right]^{-1}\left[f_{i^*k}\right]\end{array}\right]}_{B} \underbrace{\left[\begin{array}{c}F_z\\F_\phi\\F_\theta\end{array}\right]}_{\vec\tau}$
$+\underbrace{ \left[\begin{array}{cc} 0_{3\times1} & 0_{3\times1} \\ -\left[a_{i^*j^*}\right]^{-1}\left[h_{i^*\beta}\right] & \left[a_{i^*j^*}\right]^{-1}\left[g_{i^*\beta}\right] \end{array}\right]}_{B_w} \underbrace{\left[\begin{array}{l} H_w\sin\frac{2\pi}{T_w} t \\ H_w\cos\frac{2\pi}{T_w} t \end{array}\right]}_{{\vec w}}$

2.3 出力方程式
右舷と左舷の制御点の縦変位をそれぞれ $z_{si}$ と $z_{pi}$ とする( $i=1,2,3,4,5$ )と

$\underbrace{\left[\begin{array}{c}z\\\phi\\\theta\\\hline z_{s1} \\z_{s2} \\z_{s3} \\z_{s4} \\z_{s5} \\\hline z_{p1} \\z_{p2} \\z_{p3} \\z_{p4} \\z_{p5} \end{array}\right]}_{\vec{y}_M}= \underbrace{\left[\begin{array}{ccc|ccc} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\\hline 1 & \ell_{ys1} & -\ell_{xs1}& 0 & 0 & 0\\ 1 & \ell_{ys2} & -\ell_{xs2}& 0 & 0 & 0\\ 1 & \ell_{ys3} & -\ell_{xs3}& 0 & 0 & 0\\ 1 & \ell_{ys4} & -\ell_{xs4}& 0 & 0 & 0\\ 1 & \ell_{ys5} & -\ell_{xs5}& 0 & 0 & 0\\ \hline 1 & \ell_{yp1} & -\ell_{xp1}& 0 & 0 & 0\\ 1 & \ell_{yp2} & -\ell_{xp2}& 0 & 0 & 0\\ 1 & \ell_{yp3} & -\ell_{xp3}& 0 & 0 & 0\\ 1 & \ell_{yp4} & -\ell_{xp4}& 0 & 0 & 0\\ 1 & \ell_{yp5} & -\ell_{xp5}& 0 & 0 & 0 \end{array}\right]}_{C_M} \underbrace{\left[\begin{array}{c}z\\\phi\\\theta\\\hline w\\p\\q \end{array}\right]}_{\vec x}$

2.4 アクチュエータ
●浮体には、４つのスラスタが装備されており、 $k$ 番目( $k=1,2,3,4$ )のスラスタの推力を $F_k$ とすると、駆動力について次式の表現が可能。
$\underbrace{\left[\begin{array}{c}F_z\\F_\phi\\F_\theta\end{array}\right]}_{\vec\tau}= \underbrace{\left[\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & 1 & -1 & -1\\ -1 & 1 & 1 & -1 \end{array}\right]}_{G} \underbrace{\left[\begin{array}{c}F_1\\F_2\\F_3\\F_4\end{array}\right]}_{\vec F}$

●スラスタ駆動アンプの入力電圧からスラスタ推力までの静特性は３次関数であるが、単調増加関数であるので、逆関数（逆表）を用いて補償する。一方、動特性は２次遅れであるが、遅れは小さいものとして無視する。
●実機では、スラスタの遅れは無視できないようであるので、コントローラに１次遅れを入れて、実機遅れの影響を評価する。
●制御系設計では、望ましい駆動力 $F_z$ 、 $F_\phi$ 、 $F_\theta$ を設計する。このとき次式で各スラスタに推力配分できる。
$\underbrace{\left[\begin{array}{c}F_1\\F_2\\F_3\\F_4\end{array}\right]}_{\vec F}= \underbrace{\frac{1}{4}\left[\begin{array}{rrr} 1 & 1 & -1 \\ 1 & 1 & 1 \\ 1 & -1 & 1\\1 & -1 & -1 \end{array}\right]}_{G^\dag} \underbrace{\left[\begin{array}{c}F_z\\F_\phi\\F_\theta\end{array}\right]}_{\vec\tau}$

●スラスタ駆動アンプの入力電圧には制限がある。これによりスラスタ推力に
$F_{min}\le F_k\le F_{max}\quad(k=1,2,3,4)$
のような制限がかかる。この制限がないときは、 $G'G=I_3$ より、望ましい駆動力が直接働く。一方、この制限があるときは、上下限の間を往復するような制御動作を受け入れ、結果次第とすることが行なわれる。ただしその際、制御系の安定性の補償はない。

2.5 波浪モデル
●規則波：単一波周期 $T_w=\frac{2\pi}{\omega_w}$ のとき
$\underbrace{\frac{d}{dt}\left[\begin{array}{c}x_{w1}\\x_{w2}\end{array}\right]}_{\dot{\vec{x}}_w}= \underbrace{\left[\begin{array}{cc}0 & 1\\-\omega_w^2 & 0\end{array}\right]}_{A_w} \underbrace{\left[\begin{array}{c}x_{w1}\\x_{w2}\end{array}\right]}_{\vec{x}_w},\ \left[\begin{array}{c}x_{w1}(0)\\x_{w2}(0)\end{array}\right]=\left[\begin{array}{c}0\\H_w\omega_w\end{array}\right]$
⇒ $\left[\begin{array}{cc}1 & 0 \\ 0& \frac{1}{\omega_w}\end{array}\right] \underbrace{\left[\begin{array}{c}x_{w1}\\x_{w2}\end{array}\right]}_{\vec{x}_w}= \underbrace{\left[\begin{array}{l} H_w\sin\omega_w t \\ H_w\cos\omega_w t \end{array}\right]}_{\vec w}$
●不規則波：複数波周期 $T_w^{(i)}=\frac{2\pi}{\omega_w^{(i)}}\ (i=1,...,n_w)$ のとき
$\underbrace{\frac{d}{dt}\left[\begin{array}{c}{\vec x}_{w1}\\{\vec x}_{w2}\end{array}\right]}_{\dot{\vec{x}}_w}= \underbrace{\left[\begin{array}{cc}0_{n_w\times n_w} & I_{n_w}\\-\Omega_w^2 & 0_{n_w\times n_w}\end{array}\right]}_{A_w} \underbrace{\left[\begin{array}{c}{\vec x}_{w1}\\{\vec x}_{w2}\end{array}\right]}_{\vec{x}_w},\ \left[\begin{array}{c}{\vec x}_{w1}(0)\\{\vec x}_{w2}(0)\end{array}\right]=\left[\begin{array}{c}0_{n_w\times 1}\\H_w\Omega_w{\bf 1}_{n_w}\end{array}\right]$
⇒ $\left[\begin{array}{ccc|ccc}c_1& \cdots & c_{n_w} & 0& \cdots & 0 \\ 0& \cdots & 0 &c_1\frac{1}{\omega_w^{(1)}}& \cdots & c_{n_w}\frac{1}{\omega_w^{(n_w)}}\end{array}\right] \underbrace{\left[\begin{array}{c}{\vec x}_{w1}\\{\vec x}_{w2}\end{array}\right]}_{\vec{x}_w}$
$=\left[\begin{array}{l} c_1H_w\sin\omega_w^{(1)}t+\cdots+c_{n_w}H_w\sin\omega_w^{(n_w)}t \\ c_1H_w\cos\omega_w^{(1)}t+\cdots+c_{n_w}H_w\cos\omega_w^{(n_w)}t \end{array}\right]$
ここで、係数 $c_1,\cdots,c_{n_w}$ は波浪スペクトラムに従うものとする。

3.制御目的
3.1 横波中
●各波周波数の規則波または不規則波において、波上側（右舷starboard）の任意の制御点の縦変位 $z_{si}$ の動揺を抑制
3.2 斜波中
●各波周波数の規則波または不規則波において、波上側（右舷starboard）の着目する制御点の縦変位 $z_{si}$ の動揺を抑制
●各波周波数の規則波または不規則波において、波下側（左舷portside）の着目する制御点の縦変位 $z_{pi}$ の動揺を抑制

4.制御系設計
4.1 LQ制御/H∞制御
●制御対象（ $\vec{u}=\vec{\tau}$ と置き換えている）
$\left\{\begin{array}{l} \dot{\vec x}=A{\vec x}+B{\vec u}+B_w{\vec w},\ {\vec x}(0)={\vec x}_0\\ {\vec y}_M=C_M{\vec x}\\ y=\underbrace{C_SC_M}_{C}{\vec x} \end{array}\right.$
ただし、 ${y}$ は制御点の縦変位（ロールを選ぶ場合もある）
●外乱信号
${\vec w}=\left[\begin{array}{l} H_w\sin\frac{2\pi}{T_w} t \\ H_w\cos\frac{2\pi}{T_w} t \end{array}\right]$
●安定化制御則：状態FB
$\underbrace{\left[\begin{array}{c}F_z\\F_\phi\\F_\theta\end{array}\right]}_{\vec u}=- \underbrace{\left[\begin{array}{cccccc} f_{11} & f_{12} & f_{13} & f_{14} & f_{15} & f_{16} \\ f_{21} & f_{22} & f_{23} & f_{24} & f_{25} & f_{26} \\ f_{31} & f_{32} & f_{33} & f_{34} & f_{35} & f_{36} \\ \end{array}\right]}_{F} \underbrace{\left[\begin{array}{c}z\\\phi\\\theta\\\hline w\\p\\q \end{array}\right]}_{\vec x}$
●閉ループ系
$\left\{\begin{array}{l} \dot{\vec x}=\underbrace{(A-BF)}_{A_F}{\vec x}+B_w{\vec w}\\ {y}={C}{\vec x} \end{array}\right.$
この外乱応答（周波数応答）の振幅が低減されるかどうかが問われている。
●安定化状態FBを求める手段として、LQ制御則とH∞制御則の２通りが考えられる。
●LQ制御則を求める２次形式評価関数
横波中
$\displaystyle{J=\int_0^\infty(\underbrace{\frac{1}{M_{si}^2}z_{si}^2+\frac{1}{M_{\phi}^2}\phi^2+\frac{1}{M_{\theta}^2}\theta^2}_{{\vec x}^TQ{\vec x}} +\underbrace{\frac{1}{M_{F_z}^2}{F_z}^2+\frac{1}{M_{F_\phi}^2}{F_\phi}^2+\frac{1}{M_{F_\theta}^2}{F_\theta}^2}_{{\vec u}^TR{\vec u}})\,dt}$
斜波中
$\displaystyle{J=\int_0^\infty(\underbrace{\frac{1}{M_{z_{si}}^2}z_{si}^2+\frac{1}{M_{\phi}^2}\phi^2+\frac{1}{M_{\theta}^2}\theta^2}_{{\vec x}^TQ{\vec x}} +\underbrace{\frac{1}{M_{F_z}^2}{F_z}^2+\frac{1}{M_{F_\phi}^2}{F_\phi}^2+\frac{1}{M_{F_\theta}^2}{F_\theta}^2}_{{\vec u}^TR{\vec u}})\,dt}$
$\displaystyle{J=\int_0^\infty(\underbrace{\frac{1}{M_{z_{pi}}^2}z_{pi}^2+\frac{1}{M_{\phi}^2}\phi^2+\frac{1}{M_{\theta}^2}\theta^2}_{{\vec x}^TQ{\vec x}} +\underbrace{\frac{1}{M_{F_z}^2}{F_z}^2+\frac{1}{M_{F_\phi}^2}{F_\phi}^2+\frac{1}{M_{F_\theta}^2}{F_\theta}^2}_{{\vec u}^TR{\vec u}})\,dt}$
●LQ制御ゲインの計算式
$\Pi A+A^T\Pi -\Pi BR^{-1}B^T\Pi+C^TQC=0$
$F=R^{-1}B^T\Pi$
●この求解式はインパルス外乱に対する応答に対して２次形式評価関数を最小化して得られており、上の正弦波外乱に対する応答に対しても効果があるかは、着目する制御点までのゲイン線図を求めるなどして検討すべきである。
●H∞制御則
H∞制御則を用いると、外乱から着目する制御点まのゲイン線図のピーク値を確実に低減できる。ただ、これも状態FBであることから、LQ制御系と同様に閉ループ系の極( $A_F$ 固有値）を調整していることになる。計算は連立線形行列不等式を制約条件にもちH∞ノルムを低減する最適化問題を数値的に解くことになる。
●外乱応答
$e^{j\omega_w t}=\cos\omega_w t+j\sin\omega_w t$ に対する応答を計算すると
${y}=C\underbrace{\exp(A_Ft)}_{\rightarrow 0\ (t\rightarrow\infty)} (j\omega_w I-A_F)^{-1}B_w+\underbrace{C(j\omega_w I-A_F)^{-1}B_w}_{G(j\omega_w) =|G(j\omega_w)|e^{j\angle G(j\omega_w)}}e^{j\omega_w t}$
ここで、 $A_F$ は漸近安定行列であることから第１項は消滅する。第２項は
$\begin{array}{l} |G(j\omega_w)|e^{j(\omega_w t+\angle G(j\omega_w))}\\ =|G(j\omega_w)|\cos(\omega_w t+\angle G(j\omega_w))+j|G(j\omega_w)|\sin(\omega_w t+\angle G(j\omega_w)) \end{array}$
となり、定常応答を表している。 $\omega_w$ が $G(j\omega_w)$ の零点ならば外乱影響は遮断されるが、一般には難しい。
4.2 LQ-IM制御/H∞-IM制御
●内部モデル原理(Internal Model Principle)：外乱を抑制したり、目標に追従すためには、そのダイナミックスをコントローラが内包する必要があるという考え方。
LQ-IM制御：LQ Control with Internal Model
H∞-IM制御：H∞ Control with Internal Model
●制御対象（ $\vec{u}=\vec\tau$ とおく）
$\left\{\begin{array}{l} \dot{\vec x}=A{\vec x}+B\vec{u}+B_w{\vec w},\ {\vec x}(0)={\vec x}_0\\ {\vec y}_M=C_M{\vec x}\\ y=\underbrace{C_SC_M}_{C}{\vec x} \end{array}\right.$
●外乱信号
${\vec w}=\left[\begin{array}{l} H_w\sin\frac{2\pi}{T_w} t \\ H_w\cos\frac{2\pi}{T_w} t \end{array}\right]$
●外乱推定に用いる観測変数
$y_d=C_d{\vec x}$
●外乱フィルタ
$\dot{\hat{\vec x}}_d=\underbrace{\left[\begin{array}{cc}0 & 1\\-\omega_w^2 & 0\end{array}\right]}_{A_d}\hat{{\vec x}}_d+\underbrace{\left[\begin{array}{cc}0 \\ \omega_w^2\end{array}\right]}_{B_d}y_d,\ \hat{\vec x}_d(0)=0_{2\times 1}$
●拡大系
$\underbrace{\frac{d}{dt}\left[\begin{array}{c}{\vec x}\\\hat{{\vec x}}_d\end{array}\right]}_{\dot{\vec x}_E} =\underbrace{\left[\begin{array}{cc}A & 0_{6\times 2} \\B_dC_d & A_d\end{array}\right]}_{A_E} \underbrace{\left[\begin{array}{c}{\vec x}\\\hat{{\vec x}}_d\end{array}\right]}_{{\vec x}_E} +\underbrace{\left[\begin{array}{c} B \\0_{2\times 3}\end{array}\right]}_{B_{E}}\vec{u} +\underbrace{\left[\begin{array}{c} B_w \\0_{2\times 2}\end{array}\right]}_{B_{Ew}}{\vec w}$
●安定化制御則：状態FB+外乱推定FF
$\vec{u}=-\underbrace{\left[\begin{array}{cc}F & F_d \end{array}\right]}_{F_E} \underbrace{\left[\begin{array}{c}{\vec x}\\\hat{{\vec x}}_d\end{array}\right]}_{{\vec x}_E} =-F\vec{x}-F_d\hat{\vec{x}}_d$
●閉ループ系
$\left\{\begin{array}{l} \underbrace{\frac{d}{dt}\left[\begin{array}{c}{\vec x}\\\hat{{\vec x}}_d\end{array}\right]}_{\dot{\vec x}_E} =\underbrace{\left[\begin{array}{cc}A-BF & -BF_d \\B_dC_d & A_d\end{array}\right]}_{A_{EF}=A_E-B_{E}F_E} \underbrace{\left[\begin{array}{c}{\vec x}\\\hat{{\vec x}}_d\end{array}\right]}_{{\vec x}_E} +\underbrace{\left[\begin{array}{c} B_w \\0_{2\times 2}\end{array}\right]}_{B_{Ew}}{\vec w}\\ {y}=\underbrace{\left[\begin{array}{cc}C & 0 \end{array}\right]}_{C_{E}}\underbrace{\left[\begin{array}{c}{\vec x}\\\hat{{\vec x}}_d\end{array}\right]}_{{\vec x}_E} \end{array}\right.$
●LQ-IM制御系では外乱影響を排除できる。これは制御則 $\vec{u}=-F\vec{x}-F_d\hat{\vec{x}}_d$ の第２項が外乱影響をキャンセルするからと考えられる。この場合も着目する制御点までのゲイン線図を計算するなどして、外乱影響をキャンセルできることを確認すべきである。
●安定化状態FBを求める手段として、LQ-IM制御則とH∞-IM制御則の２通りが考えられる。
●LQ-IM制御則を求める２次形式評価関数
横波中
$\displaystyle{J=\int_0^\infty(\underbrace{\frac{1}{M_{si}^2}z_{si}^2+\frac{1}{M_{\phi}^2}\phi^2+\frac{1}{M_{\theta}^2}\theta^2+\frac{1}{M_{x_{d1}}^2}x_{d1}^2}_{{\vec x}^TQ{\vec x}} +\underbrace{\frac{1}{M_{F_z}^2}{F_z}^2+\frac{1}{M_{F_\phi}^2}{F_\phi}^2+\frac{1}{M_{F_\theta}^2}{F_\theta}^2}_{{\vec u}^TR{\vec u}})\,dt}$
斜波中
$\displaystyle{J=\int_0^\infty(\underbrace{\frac{1}{M_{z_{si}}^2}z_{si}^2+\frac{1}{M_{\phi}^2}\phi^2+\frac{1}{M_{\theta}^2}\theta^2+\frac{1}{M_{x_{d1}}^2}x_{d1}^2}_{{\vec x}^TQ{\vec x}} +\underbrace{\frac{1}{M_{F_z}^2}{F_z}^2+\frac{1}{M_{F_\phi}^2}{F_\phi}^2+\frac{1}{M_{F_\theta}^2}{F_\theta}^2}_{{\vec u}^TR{\vec u}})\,dt}$
$\displaystyle{J=\int_0^\infty(\underbrace{\frac{1}{M_{z_{pi}}^2}z_{pi}^2+\frac{1}{M_{\phi}^2}\phi^2+\frac{1}{M_{\theta}^2}\theta^2+\frac{1}{M_{x_{d1}}^2}x_{d1}^2}_{{\vec x}^TQ{\vec x}} +\underbrace{\frac{1}{M_{F_z}^2}{F_z}^2+\frac{1}{M_{F_\phi}^2}{F_\phi}^2+\frac{1}{M_{F_\theta}^2}{F_\theta}^2}_{{\vec u}^TR{\vec u}})\,dt}$
●LQ-IM制御ゲインの計算式
$\Pi A_E+A_E^T\Pi -\Pi B_ER_E^{-1}B_E^T\Pi+C_E^TQ_EC_E=0$
$F_E=R_E^{-1}B_E^T\Pi$
●H∞-IM制御則
H∞-IM制御則を用いると、外乱から着目する制御点まのゲイン線図のピーク値を確実に低減できる。ただ、これも状態FBであることから、LQ-IM制御系と同様に閉ループ系の極( $A_{EF}$ 固有値）を調整していることになる。計算は連立線形行列不等式を制約条件にもちH∞ノルムを低減する最適化問題を数値的に解くことになる。

4.3 SM制御
●SM制御則
$\displaystyle{{\vec u}(t)=\underbrace{{\vec u}_\ell(t)}_{linear\ control}+\underbrace{{\vec u}_n(t)}_{switching\ component} }$
$\displaystyle{{\vec u}_\ell(t)=-\underbrace{(SB)^{-1}(SA-\Phi S)}_{L=L_{eq}+L_{phi}}{\vec x}(t) }$
$\displaystyle{{\vec u}_n(t)=-\underbrace{(SB)^{-1}\rho(t,{\vec x})}_{L_n}\frac{P_2{\vec s}(t)}{||P_2{\vec s}(t)||} }$

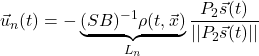
5.制御系シミュレーション
5.1 LQ制御/H∞制御（詳細はここをクリック）
●外乱から着目する制御点までの代表的なゲイン線図のピーク値は、LQ制御系とH∞制御系ともに低減されている。H∞制御系の方がより低減されている。
　

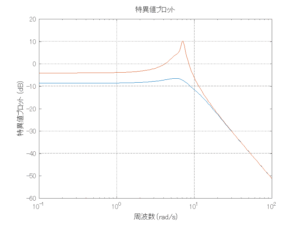
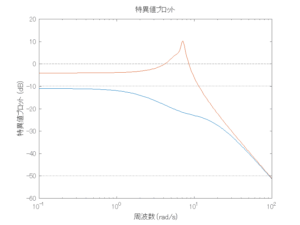
5.2 LQ-IM制御/H∞-IM制御（詳細はここをクリック）
●外乱から着目する制御点までの代表的なゲイン線図は、LQIM制御系の場合、波周波数においてピンポイントで低減され、H∞IM制御系の場合、波周波数近傍で低減されている。
　

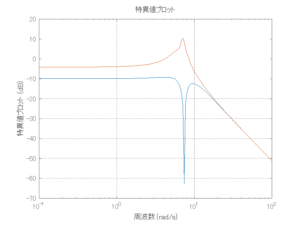
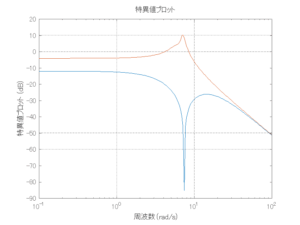
5.3 SM制御（詳細はここをクリック）
●長周期波浪影響の抑制があまりできていない。

5.4 非線形シミュレーション（詳細はここをクリック）

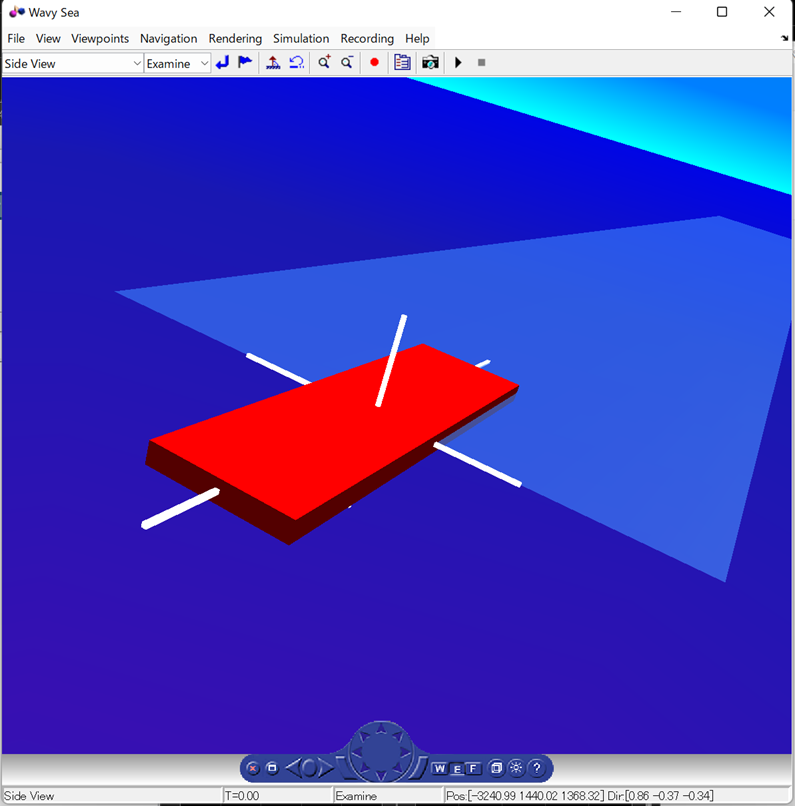
●スラスタの時間遅れを入れると制御性能が劣化する。

6.制御系実験結果

波周期6sec相当でLQ-LM制御を行ったときの実験ビデオを次に示す。

7.おわりに

付録1
●運動学

$\left\{\begin{array}{l} \dot{x}=C_\psi C_\theta u+(C_\psi S_\theta S_\phi-S_\psi C_\phi)v+(S_\psi S_\phi+C_\psi C_\phi S_\theta)w \\ \dot{y}=S_\psi C_\theta u+(C_\psi C_\phi+S_\phi S_\theta S_\phi)v+(S_\theta S_\psi C_\phi-C_\psi S_\phi)w \\ \dot{z}=-S_\theta u+ C_\theta S_\phi v + C_\theta C_\phi w\\ \dot{\phi}=p+S_\phi T_\theta q+C_\phi T_\theta r\\ \dot{\theta}=C_\phi q - S_\phi r\\ \dot{\psi}=\frac{S_\phi}{C_\theta}q+\frac{C_\phi}{C_\theta}r \end{array}\right.$
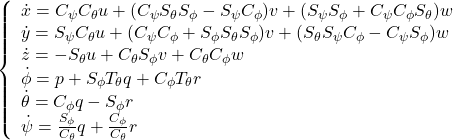
すなわち
$\frac{d}{dt}\underbrace{\left[\begin{array}{c}x\\y\\z\\\phi\\\theta\\\psi\end{array}\right]}_{\vec\eta} =\underbrace{\left[\begin{array}{cc}R_1(\phi,\theta,\psi) & 0_{3\times 3}\\0_{3\times 3} & R_2(\phi,\theta,\psi) \end{array}\right]}_{R(\phi,\theta,\psi)} \underbrace{\left[\begin{array}{c}u\\v\\w\\p\\q\\r\\\end{array}\right]}_{\vec\nu}$
ただし
$R(\phi,\theta,\psi)=\left[\begin{array}{ccc|ccc} C_\psi C_\theta & C_\psi S_\theta S_\phi-S_\psi C_\phi & S_\psi S_\phi+C_\psi C_\phi S_\theta & 0 & 0 & 0\\ S_\psi C_\theta & C_\psi C_\phi+S_\phi S_\theta S_\phi & S_\theta S_\psi C_\phi-C_\psi S_\phi & 0 & 0 & 0\\ -S_\theta & C_\theta S_\phi & C_\theta C_\phi & 0 & 0 & 0\\\hline 0 & 0 & 0 & 1 & S_\phi T_\theta &C_\phi T_\theta\\ 0 & 0 & 0 &0 & C_\phi & -S_\phi\\ 0 & 0 & 0 &0 & \frac{S_\phi}{C_\theta} & \frac{C_\phi}{C_\theta}\\ \end{array}\right]$

$\phi,\theta,\psi\simeq 0$ のときは、 $R(\phi,\theta,\psi)\simeq I_6$ より、 ${\vec\nu}\simeq \dot{\vec\eta}$ としてよい。

●運動方程式
$[a_{ij}]\underbrace{\left[\begin{array}{c}\dot{u}\\\dot{v}\\\dot{w}\\\dot{p}\\\dot{q}\\\dot{r}\end{array}\right]}_{\dot{\vec\nu}} +[b_{ij}]\underbrace{\left[\begin{array}{c}u\\v\\w\\p\\q\\r\\\end{array}\right]}_{\vec\nu} +[c_{ij}]\underbrace{\left[\begin{array}{c}x\\y\\z\\\phi\\\theta\\\psi\\\end{array}\right]}_{\vec\eta}= [f_{ik}]\underbrace{\left[\begin{array}{c}F_z\\F_\phi\\F_\theta\end{array}\right]}_{\vec\tau} +[g_{i\beta}]\cos\omega t-[h_{i\beta}]\sin\omega t$

●状態方程式
$\frac{d}{dt}\left[\begin{array}{c}x\\y\\z\\\phi\\\theta\\\psi\\\hline u\\v\\w\\p\\q\\r\\\end{array}\right]= \left[\begin{array}{cc}0_{6\times6} & R(\phi,\theta,\psi)\\-[a_{ij}]^{-1}[c_{ij}] & -[a_{ij}]^{-1}[b_{ij}] \end{array}\right] \left[\begin{array}{c}x\\y\\z\\\phi\\\theta\\\psi\\\hline u\\v\\w\\p\\q\\r\\\end{array}\right]$
$+\left[\begin{array}{c} 0_{6\times3} \\ \left[a_{ij}\right]^{-1}\left[f_{ik}\right]\end{array}\right] \left[\begin{array}{c}F_z\\F_\phi\\F_\theta\end{array}\right]$
$\begin{array}{l} +\left[\begin{array}{c} 0_{6\times1} \\ \left[a_{ij}\right]^{-1}\left[g_{i\beta}\right]\end{array}\right]\right]\end{array}\right]\cos\omega t \begin{array}{l} -\left[\begin{array}{c} 0_{6\times1} \\ \left[a_{ij}\right]^{-1}\left[h_{i\beta}\right]\end{array}\right]\right]\end{array}\right]\sin\omega t$

●周波数応答
次の漸近安定な１入力１出力 $n$ 次系の状態空間表現を考える。
$\left\{\begin{array}{ll} \dot{x}(t)=Ax(t)+Bu(t)&(x(t)\in{\rm\bf R}^n,u(t)\in{\rm\bf R})\\ y(t)=Cx(t)&(y(t)\in{\rm\bf R}) \end{array}\right.$
このとき、正弦波入力 $u(t)=\sin\omega t$ に対する零状態応答を計算する。簡単のため
$u(t)=e^{j\omega t}=\cos(\omega t)+j\sin(\omega t)$
を、零状態応答の式
$\displaystyle{y(t)=\int_0^tC\exp(A(t-\tau))Bu(\tau)d\tau}$
に代入して
$\begin{array}{l} \displaystyle{y(t)=\int_0^tC\exp(A(t-\tau))Be^{j\omega\tau}d\tau}\\ \displaystyle{=C\exp(At)\int_0^te^{j\omega\tau}\exp(-A\tau)Bd\tau}\\ \displaystyle{=C\exp(At)\int_0^t\exp(j\omega\tau I_n)\exp(-A\tau)Bd\tau}\\ \displaystyle{=C\exp(At)\int_0^t\exp((j\omega I_n-A)\tau)Bd\tau}\\ \displaystyle{=C\exp(At) \left[\frac{}{}\exp((j\omega I_n-A)\tau)\right]_0^t(j\omega I_n-A)^{-1}B}\\ \displaystyle{=C\exp(At) (\exp((j\omega I_n-A)t)-I_n)(j\omega I_n-A)^{-1}B}\\ \displaystyle{=-C\exp(At)(j\omega I_n-A)^{-1}B+C\exp(At)\exp(j\omega t I_n)\exp(-At)(j\omega I_n-A)^{-1}B}\\ \displaystyle{=-C\exp(At)(j\omega I_n-A)^{-1}B+C(j\omega I_n-A)^{-1}Be^{j\omega t}} \end{array}$
ここで $t\rightarrow\infty$ とすると
$\begin{array}{l} \displaystyle{y(t)=C\underbrace{\exp(At)}_{\rightarrow 0\ (t\rightarrow\infty)}(j\omega I_n-A)^{-1}B+\underbrace{C(j\omega I_n-A)^{-1}B}_{G(j\omega) =|G(j\omega)|e^{j\angle G(j\omega)}}e^{j\omega t}}\\ \displaystyle{\simeq |G(j\omega)|e^{j(\omega t+\angle G(j\omega))}}\\ \displaystyle{=|G(j\omega)|\cos(\omega t+\angle G(j\omega))+j|G(j\omega)|\sin(\omega t+\angle G(j\omega))} \end{array}$
これから正弦波入力に対する零状態応答は、 $t\rightarrow\infty$ のとき次式で与えられる。
$y(t)\simeq|G(j\omega)|\sin(\omega t+\angle G(j\omega))$
これは、入力が正弦波のときは、時間が十分立てば、出力も正弦波となることを示す。その振幅と位相はそれぞれ $\hat{G}(j\omega)$ の絶対値と偏角となっている。

付録2
●内部モデル原理(Internal Model Principle)：外乱を抑制したり、目標に追従すためには、そのダイナミックスをコントローラが内包する必要があるという考え方。
LQ-mIM制御：LQ Control with Internal Models
H∞-mIM制御：H∞ Control with Internal Models
●制御対象（ $\vec{u}=\vec\tau$ とおく）
$\left\{\begin{array}{l} \dot{\vec x}=A{\vec x}+B\vec{u}+B_w{\vec w},\ {\vec x}(0)={\vec x}_0\\ {\vec y}_M=C_M{\vec x}\\ y=\underbrace{C_SC_M}_{C}{\vec x} \end{array}\right.$
●外乱信号(複数波周期 $T_w^{(i)}=\frac{2\pi}{\omega_w^{(i)}}\ (i=1,...,n_w)$ のとき)
${\vec w} =\left[\begin{array}{l} c_1H_w\sin\omega_w^{(1)}t+\cdots+c_{n_w}H_w\sin\omega_w^{(n_w)}t \\ c_1H_w\cos\omega_w^{(1)}t+\cdots+c_{n_w}H_w\cos\omega_w^{(n_w)}t \end{array}\right]$
●外乱推定に用いる観測変数
$y_d=C_d{\vec x}$
●外乱フィルタ
$\dot{\hat{\vec x}}_d=\underbrace{\left[\begin{array}{cc}0_{n_w\times n_w} & I_{n_w}\\-\Omega_w^2 & 0_{n_w\times n_w}\end{array}\right]}_{A_d}\hat{{\vec x}}_d+\underbrace{\left[\begin{array}{cc}0_{n_w\times 1} \\ \Omega_w^2{\bf 1}_{n_w}\end{array}\right]}_{B_d}y_d,\ \hat{\vec x}_d(0)=0_{2n_w\times1}$
●拡大系
$\underbrace{\frac{d}{dt}\left[\begin{array}{c}{\vec x}\\\hat{{\vec x}}_d\end{array}\right]}_{\dot{\vec x}_E} =\underbrace{\left[\begin{array}{cc}A & 0_{6\times 2n_w} \\B_dC_d & A_d\end{array}\right]}_{A_E} \underbrace{\left[\begin{array}{c}{\vec x}\\\hat{{\vec x}}_d\end{array}\right]}_{{\vec x}_E} +\underbrace{\left[\begin{array}{c} B \\0_{2n_w\times 3}\end{array}\right]}_{B_{E}}\vec{u} +\underbrace{\left[\begin{array}{c} B_w \\0_{2n_w\times 2}\end{array}\right]}_{B_{Ew}}{\vec w}$
●安定化制御則：状態FB+外乱推定FF
$\vec{u}=-\underbrace{\left[\begin{array}{cc}F & F_d \end{array}\right]}_{F_E} \underbrace{\left[\begin{array}{c}{\vec x}\\\hat{{\vec x}}_d\end{array}\right]}_{{\vec x}_E} =-F\vec{x}-F_d\hat{\vec{x}}_d$
●閉ループ系
$\left\{\begin{array}{l} \underbrace{\frac{d}{dt}\left[\begin{array}{c}{\vec x}\\\hat{{\vec x}}_d\end{array}\right]}_{\dot{\vec x}_E} =\underbrace{\left[\begin{array}{cc}A-BF & -BF_d \\B_dC_d & A_d\end{array}\right]}_{A_{EF}=A_E-B_{E}F_E} \underbrace{\left[\begin{array}{c}{\vec x}\\\hat{{\vec x}}_d\end{array}\right]}_{{\vec x}_E} +\underbrace{\left[\begin{array}{c} B_w \\0_{2n_w\times 2}\end{array}\right]}_{B_{Ew}}{\vec w}\\ {y}=\underbrace{\left[\begin{array}{cc}C & 0 \end{array}\right]}_{C_{E}}\underbrace{\left[\begin{array}{c}{\vec x}\\\hat{{\vec x}}_d\end{array}\right]}_{{\vec x}_E} \end{array}\right.$
●LQ-IM制御系では外乱影響を排除できる。これは制御則 $\vec{u}=-F\vec{x}-F_d\hat{\vec{x}}_d$ の第２項が外乱影響をキャンセルするからと考えられる。この場合も着目する制御点までのゲイン線図を計算するなどして、外乱影響をキャンセルできることを確認すべきである。
●安定化状態FBを求める手段として、LQ-mIM制御則とH∞-mIM制御則の２通りが考えられる。
●LQ-mIM制御則を求める２次形式評価関数
横波中
$\displaystyle{J=\int_0^\infty(\underbrace{\frac{1}{M_{si}^2}z_{si}^2+\frac{1}{M_{\phi}^2}\phi^2+\frac{1}{M_{\theta}^2}\theta^2+\frac{1}{M_{x_{d1}}^2}x_{d1}^2}_{{\vec x}^TQ{\vec x}} +\underbrace{\frac{1}{M_{F_z}^2}{F_z}^2+\frac{1}{M_{F_\phi}^2}{F_\phi}^2+\frac{1}{M_{F_\theta}^2}{F_\theta}^2}_{{\vec u}^TR{\vec u}})\,dt}$
斜波中
$\displaystyle{J=\int_0^\infty(\underbrace{\frac{1}{M_{z_{si}}^2}z_{si}^2+\frac{1}{M_{\phi}^2}\phi^2+\frac{1}{M_{\theta}^2}\theta^2+\frac{1}{M_{x_{d1}}^2}x_{d1}^2}_{{\vec x}^TQ{\vec x}} +\underbrace{\frac{1}{M_{F_z}^2}{F_z}^2+\frac{1}{M_{F_\phi}^2}{F_\phi}^2+\frac{1}{M_{F_\theta}^2}{F_\theta}^2}_{{\vec u}^TR{\vec u}})\,dt}$
$\displaystyle{J=\int_0^\infty(\underbrace{\frac{1}{M_{z_{pi}}^2}z_{pi}^2+\frac{1}{M_{\phi}^2}\phi^2+\frac{1}{M_{\theta}^2}\theta^2+\frac{1}{M_{x_{d1}}^2}x_{d1}^2}_{{\vec x}^TQ{\vec x}} +\underbrace{\frac{1}{M_{F_z}^2}{F_z}^2+\frac{1}{M_{F_\phi}^2}{F_\phi}^2+\frac{1}{M_{F_\theta}^2}{F_\theta}^2}_{{\vec u}^TR{\vec u}})\,dt}$
●LQ-mIM制御ゲインの計算式
$\Pi A_E+A_E^T\Pi -\Pi B_ER_E^{-1}B_E^T\Pi+C_E^TQ_EC_E=0$
$F_E=R_E^{-1}B_E^T\Pi$
●H∞-mIM制御則
H∞-mIM制御則を用いると、外乱から着目する制御点まのゲイン線図のピーク値を確実に低減できる。ただ、これも状態FBであることから、LQ-mIM制御系と同様に閉ループ系の極( $A_{EF}$ 固有値）を調整していることになる。計算は連立線形行列不等式を制約条件にもちH∞ノルムを低減

制御系CAD

制御を意識したモノつくりを目指して

浮体制御(非公開)